ВСТУП

Курс «Теорія ймовірностей і математична статистика» складається із двох математичних дисциплін .

Теорія ймовірностей вивчає явища – випадкові події, величини, процеси – з точки зору їх кількісного аналізу. Курс можна умовно поділити на три частини: класичний розділ, схема випробувань Бернуллі та основні наближені формули, випадкові величини, способи їх задавання та основні числові характеристики.

Класичний розділ є базовим для розуміння основних понять і сутності теорії ймовірностей та ґрунтується на курсі елементарної математики. У цьому розділі вводяться класичне означення ймовірності випадкової події, основні види випадкових подій, операції над подіями та основні теореми для обчислення ймовірностей подій, які виражаються через інші події за допомогою операцій.

У другому розділі розглядається один із основних способів організації експерименту – схема незалежних випробувань Бернуллі. Вводяться класична формула Бернуллі та відповідні наближені формули.

У третьому розділі вводиться одне з основних понять теорії ймовірностей – випадкова величина, яка дозволяє перейти від класичного розділу та елементарних методів вивчення випадкових подій до застосування потужного апарату математичного аналізу для дослідження випадкових явищ. У цьому розділі розглядаються основні закони розподілу випадкових величин – Бернуллі, Пуассона, геометричний, нормальний – та практичні задачі, які до них приводять.

Математична статистика – це математична дисципліна, яка вивчає випадкові явища, використовуючи практичні результати випробувань або спостережень за випадковою величиною (вибірку). Теоретичним підґрунтям математичної статистики є теорія ймовірностей. До програми входить знайомство з основними задачами математичної статистики: оцінюванням невідомого закону розподілу досліджуваної випадкової величини, знаходженням оцінок його невідомих параметрів та перевіркою статистичних гіпотез, які висуваються відносно випадкової величини.

Предмет тй

Події бувають вірогідні, неможливі і випадкові. Випадкові подія – така подія, при багаторазовому відтворенні досліду якої перебіг процесу кожного разу різний.

ТЙ – розділ математики, в якому вивчають закономірності випадкових подій.

Статистичне значення тй

Випробування – конкретна реалізація досліду, яка може вибиратися при даних безліч разів.

Частка події А в перших п випробуваннях – відношення числа настання події в цих випробуваннях до числа п випробувань

Ймовірні події – границя частки при необмеженому збільшенні числа випробувань . Це визначення базується на ідеалізації реальності.

Статистична Й – Й події А, яка обчислюється на основі випробувань.

Прості елементарних подій

Елементарна подія (ЕП) – наслідок випробування .

Простір елементарних подій – множина наслідків випробувань

Відношення між подіями

Нехай А – подія, яка може відбутись або не відбутись у даному випробуванні. Факт відбування події А визначається Якщо при даному подія А відбувається, то елементарний наслідок сприяє події А; якщо при даному подія А не відбувається, то не сприяє А.

Нехай множина наслідків, які сприяють події А. Наслідки утворюють підмножину простору елементарних наслідків .

Вірогідна подія - - подія ,якій не сприяють усі елементарні наслідки .

Неможлива подія – Ø – подія, якій не сприяє ніякий елементарний наслідок.

Подія , яка протилежна події А – якій сприяють , які не сприяють події А: інколи доповнення до .

Об’єднані (сума) подій А і В – подія, яка полягає в тому, що відбувається хоча б одна з них А або В.

Різниця А\В подій А і В – подія, якій сприяють ті і тільки ті , які сприяють події А і не сприяють події В.

Добуток (перетин) подій А і В: подія, яка полягає в настанні обох подій одночасно.

Несумісні події А і В, якщо Ø.

Діаграми Ейлера-Венна.

Подія В є наслідком події А: , якщо усі , які сприяють А, сприяють і В. Якщо і , то події А і В називаються рівними, тобто

Властивості операцій

1. Комутативність:

2. Асоціативність:

3. Дистрибутивність:

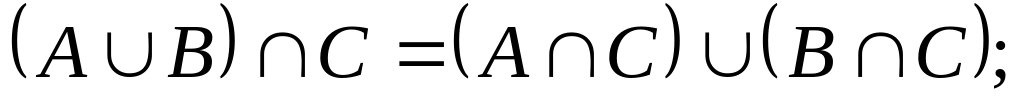
Деякі операції над подіями:

Ø; Ø Ø= Ø;

Якщо то

Приклади.

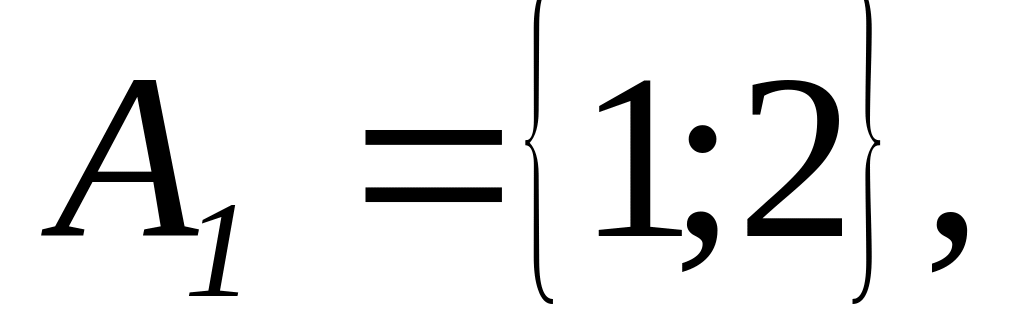
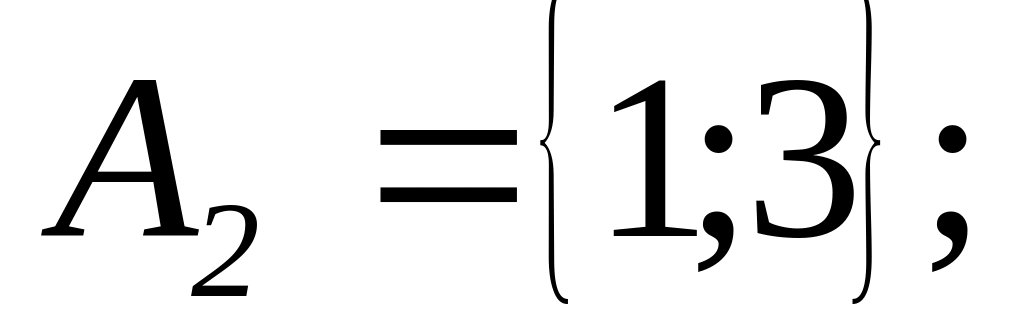
1. Партія складається з деталей 1, 2, 3 ґатунку і браку. Деталі ретельно перемішані. Із партії витягується 1 деталь. Розглянемо події 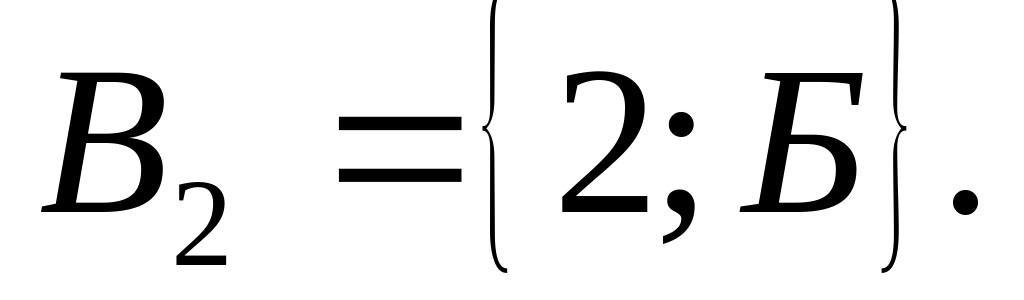Яка з подій В утворює з подіями повну групу ?

2. Визначити подію де і випробування визначені в п. 1

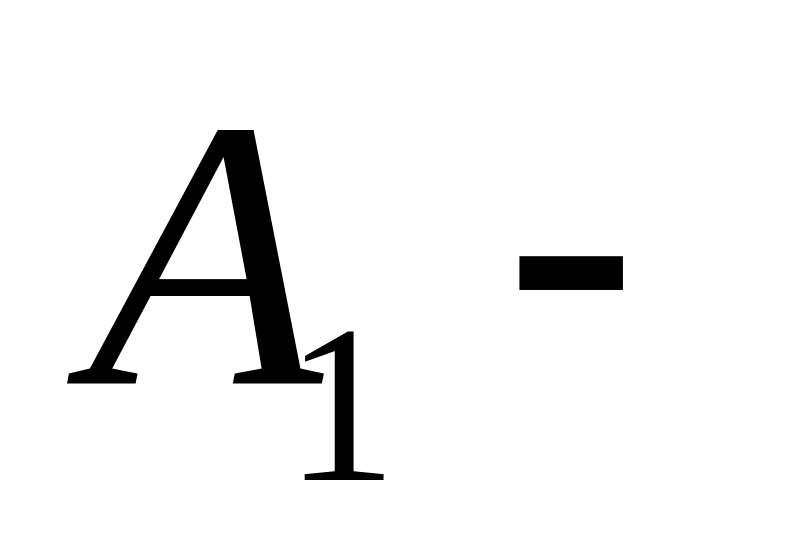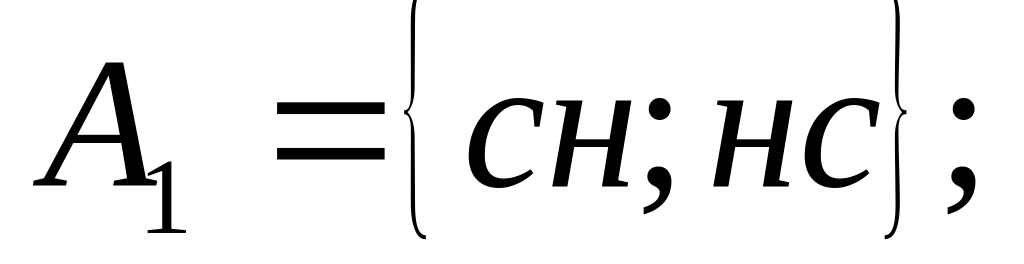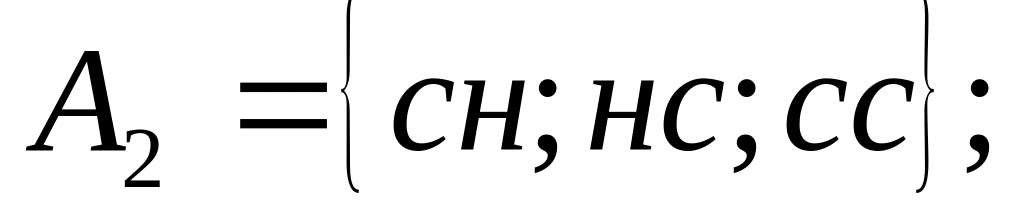3. Партія складається зі стандартних (С) і нестандартних (Н) деталей. Навмання вибирають дві деталі по одній з поверненням. Визначити: 1) простір елементарних подій 2) подію поява однієї нестандартної і однієї стандартної деталей 3) поява не менше однієї стандартної деталі 4) поява не більше однієї стандартної деталі

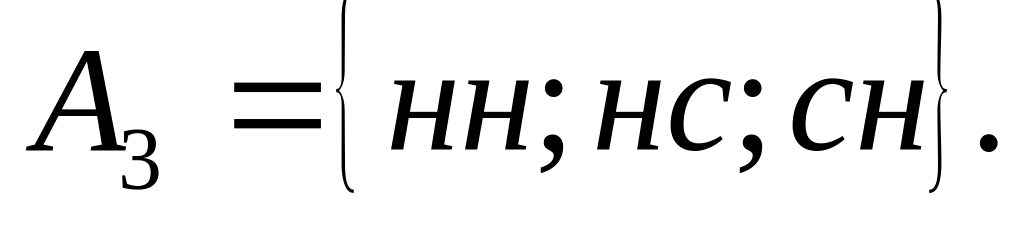
4. Із ящика, який містить бронзові (Б), латунні (Л), мідні (М) і сталеві (С) деталі навмання вибирається одна деталь: 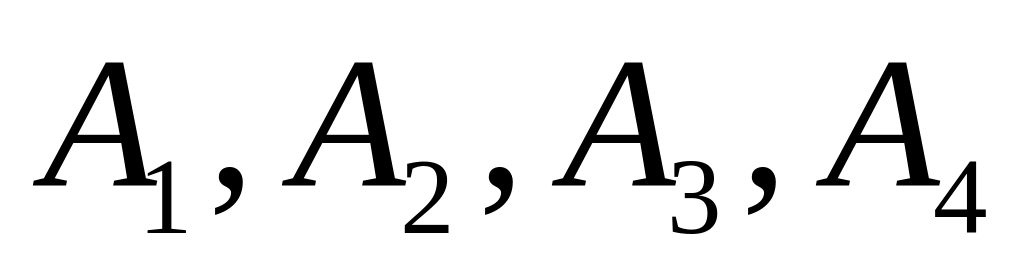відповідно позначають Б, Л, М і С деталі. Визначити подію