
- •Тема. Лінії на площині.
- •Ключові поняття і терміни:
- •Рівняння прямої на площині
- •Рівняння прямої,що проходить через дану точку перпендикулярно до даного вектора
- •Рівняння прямої з кутовим коефіцієнтом
- •Рівняння прямої, яка проходить через дану точку в даному напрямі
- •Канонічне рівняння прямої
- •Рівняння прямої, що проходить через дві задані точки
- •Рівняння прямої у відрізках
- •Загальне рівняння прямої
- •Запитання і завдання
Канонічне рівняння прямої
Нехай пряма
проходить через задану точку M0(x0;
у0)
паралельно даному векторові ![]() = (l,
m)
(рис. 3.8).
= (l,
m)
(рис. 3.8).

Виберемо на прямій
довільну точку М (х; у) і розглянемо
вектор M0M
=(х-х0,у-у0).
Вектори
![]() і
колінеарні, тому їхні координати
пропорційні. З цієї умови дістанемо
рівняння
і
колінеарні, тому їхні координати
пропорційні. З цієї умови дістанемо
рівняння
![]() (3.9)
(3.9)
яке називають
канонічним
рівнянням прямої.
Вектор
![]() називають
напрямним вектором прямої.
називають
напрямним вектором прямої.
Рівняння прямої, що проходить через дві задані точки
Нехай пряма
проходить через дві задані точки M1(х1;
y1)
і
М2(х2,
у2)
(рис. 3.9). Тоді напрямним вектором прямої
буде
= M1M![]() = (х2
- х1,y2-y1
)- Підставивши його координати й координати
заданої точки M1
(х1;y1)
у рівняння (3.9), дістанемо рівняння
= (х2
- х1,y2-y1
)- Підставивши його координати й координати
заданої точки M1
(х1;y1)
у рівняння (3.9), дістанемо рівняння
![]() (3.10)
(3.10)
яке називають рівнянням прямої, що проходить через дві задані
точки.

Приклад 4. Запишемо рівняння прямої, що проходить через точки M1(3; 1) і M2 (5; 4),
Підставляючи координати заданих точок у рівняння (3.10), дістанемо рівняння шуканої прямої:
![]() або
або
![]() або
3x-2y-7=0
або
3x-2y-7=0
Рівняння прямої у відрізках
Запишемо рівняння прямої, яка відтинає від осей координат Ох і Oу задані відрізки α≠ 0 і Ь ≠ 0 відповідно (рис. 3.10).
Використовуючи
рівняння прямої (3.10), яка проходить
через точки А{а;0)
і B(0;
b),
дістанемо 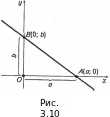 рівняння
рівняння
![]() ,або
після перетворень
,або
після перетворень
![]() (3,11)
(3,11)
Рівняння (3.11) називають рівнянням
прямої у відрізках. Його зручно використовувати під час побудови прямої.
Приклад 5. Запишемо рівняння прямої, що проходить через точку М (4; -1)і відтинає від додатної півосі Ох відрізок удвоє більший, ніж на додатній півосі Оу, й побудуємо цю пряму

За умовою а = 2Ь (а > 0, Ь > 0).
Підставивши ці значення в рівняння (3.11), дістанемо
![]()
Оскільки точка М
(4; -1) лежить на прямій, то її координати
задовольняють це рівняння. Отже
![]()
Звідси b=1. Тоді а = 2. Рівняння шуканої прямої (рис. 3.11) має вигляд
![]()
Загальне рівняння прямої
Розглянемо рівняння першого степеня відносно змінних х і у
ах + Ьу + с = 0. (3.12)
Якщо коефіцієнти а і b цього рівняння одночасно не дорівнюють нулю (а + Ь > 0), то його називають загальним рівнянням прямої. Окремі випадки рівняння (3.12) подано в табл. 3.1.

Взаємне розміщення двох прямих
□ Перетин двох прямих. Нехай задано дві прямі: а1х + b1у + с1 = 0 і а2x + b2у + с2 = 0, які перетинаються. Оскільки координати точки перетину цих прямих мають задовольняти рівняння кожної прямої, то їх можна знайти, розв'язавши систему рівнянь
![]() (3.13)
(3.13)
Якщо система (3.13) має єдиний розв'язок (х0; у0), то прямі перетинаються в точці М0 (х0; у0).
□ Кут між прямими. Нехай потрібно знайти кут, між прямими L1:y= k1х + b1 і :L2: у = k2x + b2 (рис. 3.12). Із рисунка видно, що кут між прямими L1 і L2 становить ϕ = а2 - а1. Оскільки k1 = tg а1, k2= tg а2, то за умови, що а1≠π/2 і a2≠π/2, дістанемо
![]()
або
![]() (3.14)
(3.14)
Формула (3.14) визначає один із кутів між прямими, що перетинаються. Інший кут дорівнює π-ϕ.
□ Умова паралельності прямих. Якщо прямі L1 у= k1х +b1 і L2: у = k2x + b2 паралельні, то кут ϕ = 0, а отже, tg ϕ = 0. Із формули (3.14) випливає, шо
k1=k2. (3.15)
і навпаки, якшо k1=k2, то з формули (3.14) випливає, шо tg ϕ = 0, а отже, і ϕ = 0. Таким чином, умова (3.15) є необхідною й достатньою умовою паралельності двох прямих
.
■ Приклад 6. Запишемо рівняння прямої, що проходить через точку М(-2; 4) паралельно прямій 2х - Зу + 6 = 0 (рис.3.13).

Записавши рівняння
заданої прямої у вигляді .![]() ,
знайдемо її кутовий коефіцієнт k1=
2/3. Оскільки задана й шукана прямі
паралельні, то їхні кутові коефіцієнти
рівні, тобто k1
= k2=
2/3.
,
знайдемо її кутовий коефіцієнт k1=
2/3. Оскільки задана й шукана прямі
паралельні, то їхні кутові коефіцієнти
рівні, тобто k1
= k2=
2/3.
Шукана пряма проходить через точку М(-2; 4) і має кутовий коефіцієнт k2 = 2/3. Тому її рівняння має вигляд
![]() або
або
![]()
Умова перпендикулярності двох прямих. Якщо прямі L1: у=k1x+b2 і L2;y=k2x+b2 перпендикулярні, то кут ϕ= π/2; при цьому
![]() або
або
![]() .Отже,
справедлива рівність
.Отже,
справедлива рівність
![]() (3.16)
(3.16)
Таким чином, умова (3.16) є необхідною й достатньою умовою перпендикулярності двох прямил.
□ Відстань від точки до прямої. Нехай задано точку М0(х0; у0) і пряму L: ах + bу + с = 0. Відстань від точки М0(х0; у0) до прямої L є довжиною перпендикуляра d=M0N - (рис. 3.14), яка обчислюється за формулою
![]() (3.17)
(3.17)

Приклад 7. Знайдемо відстань між двома паралельними прямими АВ: 4х + Зу - 8 = 0 і DC: 4х + Зу -33 = 0 (рис. 3.15).
Через довільну точку А на будь-якій із прямих (наприклад АВ) проведемо перпендикуляр АМ. Визначивши координати точок перетину цього перпендикуляра із заданими прямими, знайдемо відстань між цими прямими. Кутовий коефіцієнт прямої АВ
![]() .
Знайдемо кутовий коефіцієнт прямої АМ,
що проходить через точку A(2;
0) перпендикулярно до прямої АВ, з
умови (3.16):
.
Знайдемо кутовий коефіцієнт прямої АМ,
що проходить через точку A(2;
0) перпендикулярно до прямої АВ, з
умови (3.16):
![]() Отже,
рівняння цього
перпендикуляра має вигляд
Отже,
рівняння цього
перпендикуляра має вигляд
![]() або
або
![]()
Знайдемо точку
перетину перпендикуляра АМ із прямою
ОС, розв'язавши систему
![]()
Звідси дістаємо координати точки перетину M(6; 3). Обчислюємо відстань між точками А і М:
![]()
