2 Оптимизация плана работы автотранспорта при осуществлении централизованного завоза-вывоза контейнеров
Для оптимизации плана работы автотранспорта используется транспортная задача. Общая постановка транспортной задачи состоит в определение оптимального плана перевозок некоторого однородного груза из m пунктов отправления (А1, А2, Аm) в n пунктов назначения (В1, В2, Вn). В качестве критериев эффективности используются критерии пробега, времени и стоимости.
Транспортная задача записывается в виде матрицы, в которой потребитель записывается по столбцам, а поставщик - по строкам. На пересечении строк и столбцов записывается размер поставки и затраты на перевозку.
Рассмотрим
математическую модель прикрепления
пунктов назначения к пунктам отправления.
Имеется n
потребителей и m
поставщиков, мощность i-го
поставщика (i=1,
m)→
.,
спрос j-го
потребителя j
(j=1,
n)→
.
Общая сумма затрат F.
Затраты на перевозку одной тонны груза
обозначаются как Cij,
а размер поставки -
.
Математическая модель имеет вид:
,
(2.1)
Задача имеет следующие ограничения:
1) Объем поставок i-го поставщика должен равняться количеству имеющегося у него груза:
2) Объем поставок j -го потребителя должен равняться его спросу:
3) Объем поставки должен выражаться неотрицательным числом:
,
(2.4)
Условие
разрешимости транспортной задачи запас
грузов поставщиков должен равняться
суммарному спросу потребителя:
В том случае, когда модель является незакрытой, ее необходимо привести к закрытой форме. Если нет равенства в задаче, вводится фиктивный отправитель или получатель.
Расстояние между получателем и отправителем находится по формуле:
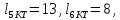
Проверим необходимое и достаточное условие разрешимости задачи.
Условие баланса не соблюдается. Задача открытая. Приводим к закрытой с помощью ввода фиктивного КТ 25-17 = 8.
Условие баланса соблюдается.
Занесем исходные данные в распределительную таблицу 2.1.
Таблица 2.1 – Распределительная таблица
|
Получатель |
П1 |
П2 |
П3 |
П4 |
П5 |
П6 |
П7 |
П8 |
Объем выгрузки |
|
О1 |
0 |
7 |
9 |
11 |
7 |
6 |
9 |
11 |
0 |
|
О2 |
7 |
0 |
8 |
4 |
2 |
5 |
8 |
10 |
1 |
|
О3 |
9 |
8 |
0 |
10 |
10 |
3 |
8 |
2 |
3 |
|
О4 |
11 |
4 |
10 |
0 |
4 |
9 |
6 |
10 |
2 |
|
О5 |
7 |
2 |
10 |
4 |
0 |
7 |
10 |
12 |
1 |
|
О6 |
6 |
5 |
3 |
9 |
7 |
0 |
7 |
5 |
4 |
|
О7 |
9 |
8 |
8 |
6 |
10 |
7 |
0 |
8 |
2 |
|
О8 |
11 |
10 |
2 |
10 |
12 |
5 |
8 |
0 |
4 |
|
КТ |
6 |
13 |
7 |
17 |
13 |
8 |
15 |
7 |
8 |
|
Объем погрузки |
2 |
0 |
2 |
5 |
5 |
2 |
4 |
5 |
25 25 |
План, при котором функция принимает свое минимальное значение, называется оптимальным планом.
Составим начальный опорный план, приведенный в таблице 2.2.
Таблица 2.2 – Опорный план транспортной задачи
Проверим опорный план на условие вырожденности / невырожденности. Число занятых клеток таблицы, их 14, а должно быть m + n - 1 = 16. Следовательно, опорный план является вырожденным. Для получения невырожденного плана принудительно добавляем нуль [0] в клетку (5;7).
Целевая функция:
Проверим оптимальность опорного плана. Найдем предварительные потенциалы ai, вj. по занятым клеткам таблицы, в которых ai + вj = cij, полагая, что a1= 0:
a1 + в1 = 0; 0 + в1 = 0; в1 = 0; a9 + в2 = 2; а9 = 2;
a3 + в4 = 1; а3 = 2; a3 + в3 = 0; в3 = -2; a4 + в4 = 2; a4 = 3;
a5 + в5 = 1; a9 + в5 = 4; в5 = 2; а5 = -1;
a5 + в7 = 0; в7 = 0;
a6 + в6 = 2; a6 + в7 = 2; в6 = 0; а6 = 2;
a7 + в7 = 2; a7 = 2;
a8 + в8 = 4; a9 + в8 = 1; a8 = 5; в8 = -1.
Опорный план не является оптимальным, так как существуют оценки свободных клеток, для которых ai + вj > cij:
(2;2): 7 + 7 > 0; ∆22 = 7 + 7 - 0 = 14 (2;4): 7 + 0 > 4; ∆24 = 7 + 0 - 4 = 3 (2;5): 7 -2 > 2; ∆25 = 7 -2 - 2 = 3 (3;2): 9 + 7 > 8; ∆32 = 9 + 7 - 8 = 8 (4;2): 0 + 7 > 4; ∆42 = 0 + 7 - 4 = 3 (5;2): 4 + 7 > 2; ∆52 = 4 + 7 - 2 = 9 (5;5): 4 -2 > 0; ∆55 = 4 -2 - 0 = 2 (6;1): 9 + 0 > 6; ∆61 = 9 + 0 - 6 = 3 (6;2): 9 + 7 > 5; ∆62 = 9 + 7 - 5 = 11 (7;1): 12 + 0 > 9; ∆71 = 12 + 0 - 9 = 3 (7;2): 12 + 7 > 8; ∆72 = 12 + 7 - 8 = 11 (7;4): 12 + 0 > 6; ∆74 = 12 + 0 - 6 = 6 (7;7): 12 -6 > 0; ∆77 = 12 -6 - 0 = 6 (8;1): 14 + 0 > 11; ∆81 = 14 + 0 - 11 = 3 (8;2): 14 + 7 > 10; ∆82 = 14 + 7 - 10 = 11 (8;3): 14 -9 > 2; ∆83 = 14 -9 - 2 = 3 (8;4): 14 + 0 > 10; ∆84 = 14 + 0 - 10 = 4 (9;1): 21 + 0 > 6; ∆91 = 21 + 0 - 6 = 15 (9;2): 21 + 7 > 13; ∆92 = 21 + 7 - 13 = 15 (9;3): 21 -9 > 7; ∆93 = 21 -9 - 7 = 5 (9;4): 21 + 0 > 17; ∆94 = 21 + 0 - 17 = 4 (9;5): 21 -2 > 13; ∆95 = 21 -2 - 13 = 6 (9;6): 21 -9 > 8; ∆96 = 21 -9 - 8 = 4 max(14,3,3,8,3,9,2,3,11,3,11,6,6,3,11,3,4,15,15,5,4,6,4) = 15
Звено неоптимальности - клетка (9;1).
С помощью программы, решим задачу методом потенциалов.
Таблица 2.4 – Оптимальный план транспортной задачи
F= 0*7 + 0*0 + 4*1 + 0*2 + 1*8 + 2*0 + 0*1 +9*2 + 0*2 + 0*7 + 0*2 + 8*1 + 0*3 + 2*6 + 13*4 + 7*2 = 116.
Расчеты экономической эффективности опорного и оптимального планов представлены в таблицах 2.5 и 2.6.
l1 – расстояние от контейнерного терминала (КТ) до грузополучателя (О); l2 – расстояние от грузополучателя (О) до грузоотправителя (П); l3 – расстояние от грузоотправителя (П) до контейнерного пункта (КТ).
Таблица 2.5 – Расчет экономической эффективности опорного плана
Таблица 2.6 – Расчет экономической эффективности оптимального плана
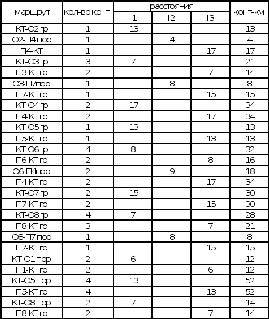
Вывод: Расчет показал, что оптимальный план, решенный методом потенциалов, равен по стоимости опорному плану.