СОДЕРЖАНИЕ

Техническое задание.....................................................................................................................3

1. Структурный анализ.....................................................................................................4

2. Геометрический анализ................................................................................................6

3. Кинематический анализ...............................................................................................9

4. Силовой анализ...........................................................................................................13

4.1. Статический анализ.....................................................................................14

4.2. Кинетостатический анализ.........................................................................19

4.2.1. Погруппный метод.......................................................................19

4.2.2. Метод возможный перемещений................................................24

Выводы........................................................................................................................................26

ТЕХНИЧЕСКОЕ ЗАДАНИЕ

Задание: для механизма насоса (рис.1.) провести структурный, геометрический, кинематический, силовой анализ.

Рис.1. Механизм насоса

Задание № 30 ж

O1A	AB	AC	BO2	CD	a	b	d		n1
мм								об/мин
100	200	200	450	620	420	120	200		150

1. Структурный анализ

1) Пронумеруем звенья механизма (рис.2.).

Рис.2. Схема механизма

2) Данный механизм (рис.2) является плоским. Определим число степеней подвижности (W) или число двигателей, необходимых для работы механизма по формуле Чебышева:

для плоского механизма , где N – число подвижных звеньев, - число низших кинематический пар, - число высших кинематических пар.

Тогда .

3) Построим граф механизма и выделим структурные группы (рис.3.)

Рис.3. Граф механизма

4) В программе «КОМПАС» с помощью функции «Параметризация» смоделируем и провернем механизм, подберем длины звеньев.

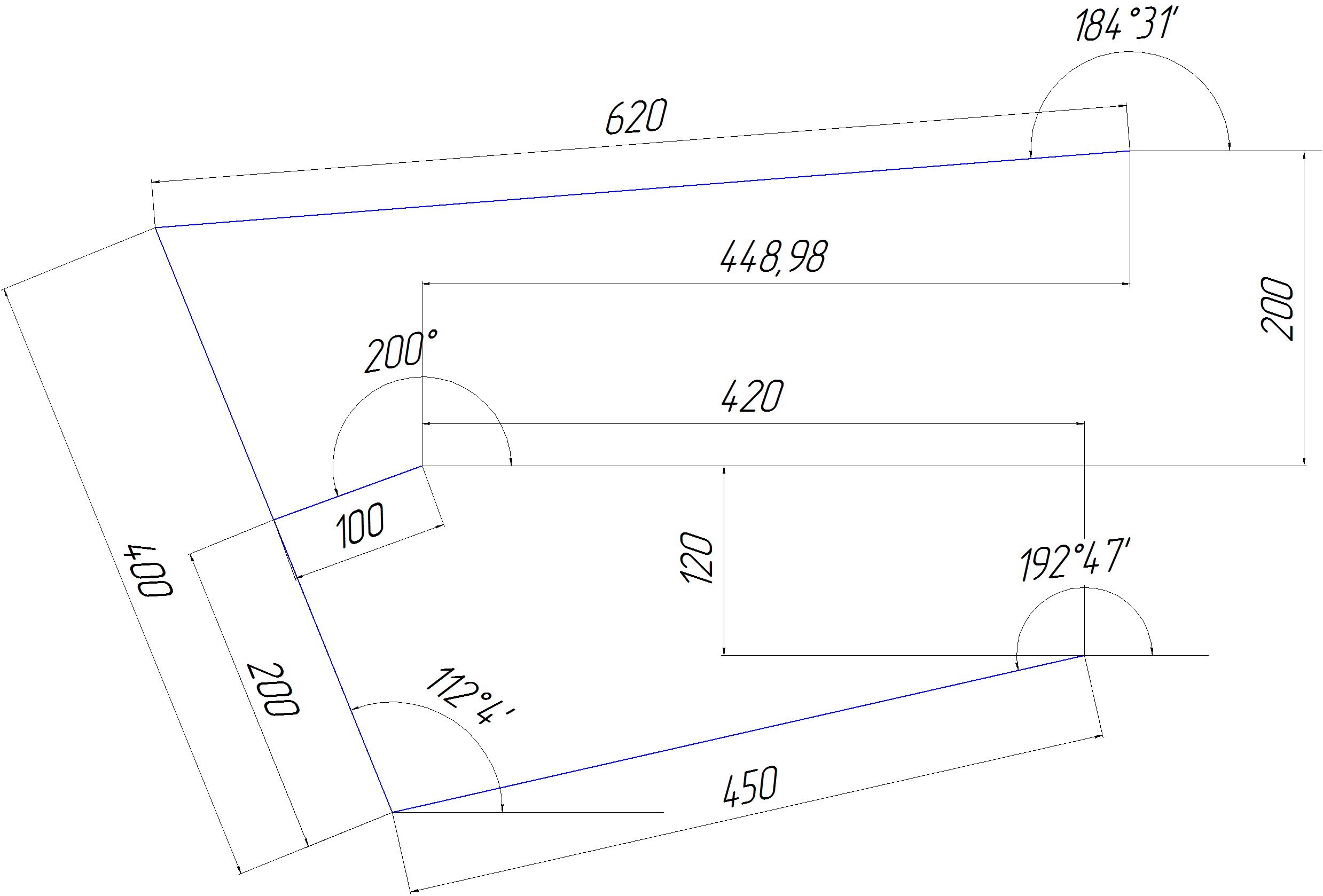
Рис.4. Параметризация механизма в программе «КОМПАС».

5) План «12-ть положений»:

Рис.5. План «12 положений».

2. Геометрический анализ

1) Для составления уравнений геометрического анализа на графе механизма

сделаем разрыв, выделим контура (рис.6).

Рис.6. Разрыв графа механизма.

2) Введем углы поворота 2-го,3-го и 4-го звеньев: и соответственно.

П роецируя вектора на оси x и y для замыкания контуров, составим уравнения геометрического анализа (см. рис.7):

Рис.7. Схема механизма для составления уравнений геометрического анализа.

Система №1 для разрыва в точке A:

, где , , , - неизвестные.

Система №2 для разрыва в точке C:

, где , , - неизвестные.

Для решения системы №1 введем вспомогательный угол .

3) Путем алгебраических преобразований решим систему №1 и №2 и построим зависимости всех неизвестных от q (в градусах).

Решение системы №1 и системы №2:

;

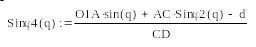
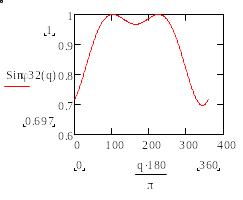
(а) (б)

Рис.8. Графики зависимости

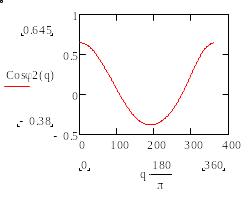
(в) (г)

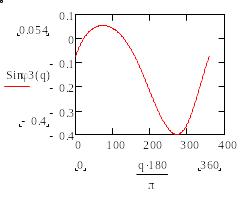
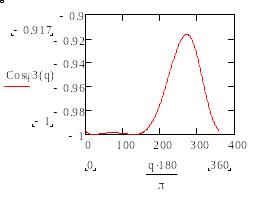
(д) (е)

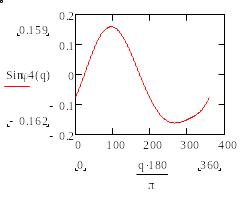
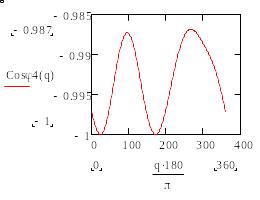
(ж) (з)

Рис.9. Графики зависимости

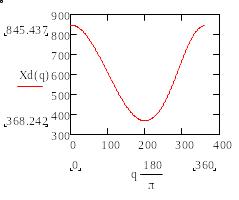
Рис.10. График зависимости

4) Выполним проверку механизма по выходной координате:

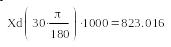
Рис.11. Проверка механизма по выходной координате при q=30^o X_d=823.

3. Кинематический анализ

1) В случаях, когда неизвестна зависимость q(t) вместо терминов «скорость» и «ускорение» используют «аналоги скорости и ускорения»:

, где - аналог скорости, который равен .

Аналогично для «аналога ускорения»:

, где - аналог ускорения, который равен .

2) Для вывода аналогов скорости продифференцируем по q системы №1 и №2:

Система №1

Получаем систему №1-1:

Из системы №1-1 выводим выражения для аналогов и (для вывода выражений введем величину ):

Аналогично дифференцируем систему №2 и выводим выражения для аналогов скоростей , . Системе №2:

Получаем систему №2-1:

Решение (для вывода выражений введем величину ):

3) Для вывода аналогов ускорения продифференцируем по q системы №1-1 и №2-1:

Система №1-1

Получаем систему №1-2:

Из системы №1-2 выводим выражения для аналогов ускорений и :

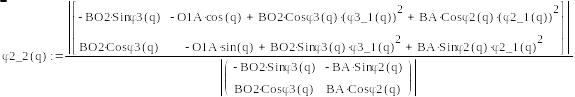
Аналогично дифференцируем систему №2-1 и выводим выражения для аналогов ускорений , .

Система №2-1

Получаем систему №2-2:

Решение:

4) Строим графики зависимости всех выведенных аналогов скоростей и ускорений от q (в градусах).

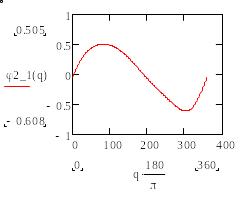
(а)

(б)

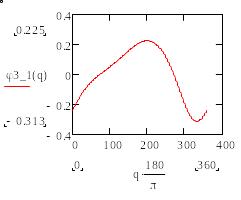
Рис.12. Графики зависимости аналогов скоростей а- , б- .

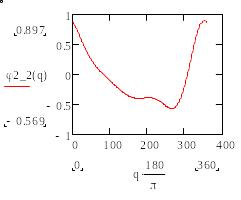
(в)

(г)

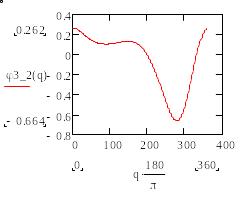
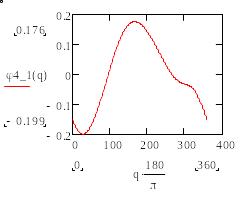
(д) (е)

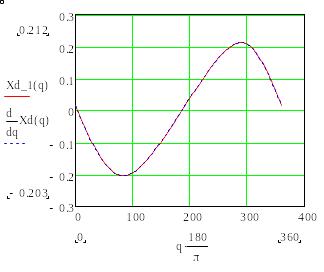
(ж) (з)

Рис.13. Графики зависимости аналогов скоростей и ускорений в- , г- ,

д- , е- , ж- , з- .