2.1.3.3 Метод двух узлов

В случае, когда в электрической схеме несколько источников ЭДС и цепь состоит из n параллельных ветвей и имеет всего два узла, расчет проще всего проводить при помощи метода двух узлов. По этому методу сначала определяют напряжение между двумя узлами схемы, а потом находят токи ветвей. Начинают с выбора условно положительного направления напряжения между узлами и обозначают его стрелкой на схеме. Напряжение между двумя узлами параллельной цепи равно алгебраической сумме произведений проводимости и ЭДС каждой ветви, деленной на сумму проводимостей всех ветвей схемы.

;

Уравнение записано для цепи имеющей n ветвей, m из которых активные, то есть содержат источники ЭДС. Произведение проводимости и ЭДС берут со знаком "плюс" в том случае, когда направление ЭДС противоположно выбранному условно положительному направлению напряжения между двумя узлами и со знаком "минус", когда эти направления совпадают. Для примера рассмотрим схему на рисунке 2.9.

Рисунок 2.9 - Пример применения метода двух узлов

Уравнение, записанное по методу двух узлов для этой схемы:

где - эквивалентная проводимость последовательно включенных сопротивлений.

2.1.3.4 Метод наложения

Метод наложения используется для расчета сложных цепей с несколькими источниками питания. Суть этого метода заключается в том, что расчет сложной цепи с несколькими источниками сводят к расчету нескольких цепей с одним источником. Ток в любой ветви исходной схемы является результатом наложения токов, получающихся от отдельных источников ЭДС, действующих независимо друг от друга.

Для примера рассмотрим цепь с двумя источниками на рисунке 2.10 а. Для определения токов в схеме методом наложения, вначале полагают, что в схеме действует только источник . При этом сопротивления всех резисторов, включая внутреннее сопротивление источника , считается неизменным. Определение частичных токов схемы от ЭДС ( , … ) сводится к расчету цепи на рисунке 2.10 б. Далее повторяют расчет для ЭДС (рисунок 2.10 в), и находят частичные токи , … . Алгебраическое суммирование частичных токов дает действительное значение токов ветвей: , … . При этом число слагаемых в последних уравнениях будет равно числу источников ЭДС в схеме.

Рисунок 2. 10 - Расчет электрической цепи методом наложения

2.1.3.5 Метод эквивалентного генератора

В некоторых случаях бывает необходимо проанализировать режим работы одной из ветвей сложной электрической цепи при изменении сопротивления этой же ветви. При этом целесообразно воспользоваться методом эквивалентного генератора. Согласно этому методу воздействие всех источников электрической цепи на исследуемую ветвь можно заменить воздействием последовательно соединенного с ветвью эквивалентного генератора, имеющего ЭДС и внутреннее сопротивление .

Для определения параметров эквивалентного генератора, исследуемую ветвь отключают от остальной схемы и с помощью любого известного метода расчета находят напряжение на зажимах схемы, к которым была подключена исследуемая ветвь. Таким образом, определяется напряжение холостого хода эквивалентного генератора, равное его ЭДС . Для определения внутреннего сопротивления эквивалентного генератора , определяют эквивалентное сопротивление схемы относительно зажимов, к которым была подключена исследуемая ветвь. Зная ЭДС и внутренне сопротивление эквивалентного генератора, можно определить ток в исследуемой ветви:

,

где R – сопротивление исследуемой ветви.

Рассмотрим применение метода эквивалентного генератора на примере схемы на рисунке 2.11 а.

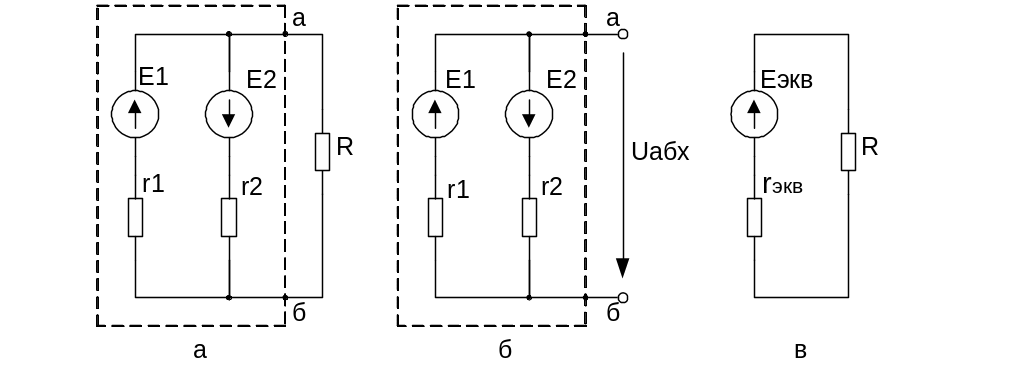
Рисунок 2.11 - Применение метода эквивалентного генератора

В схеме исследуемая ветвь с сопротивлением R подключена к зажимам "а" и "б". Отключив ветвь с сопротивлением R от схемы необходимо найти напряжение на зажимах "а" и "б" - , равное ЭДС эквивалентного генератора. Удобнее всего это сделать с помощью метода двух узлов:

.

Внутреннее сопротивление эквивалентного генератора равно сопротивлению схемы между зажимами "а" и "б" схемы рисунке 2.11 б. Так как внутреннее сопротивление идеальных источников ЭДС равно нулю, то внутреннее сопротивление генератора равно эквивалентному сопротивлению параллельно включенных сопротивлений и :

.

В результате схема может быть представлена в виде эквивалентного генератора с параметрами и и присоединенного к этому генератору сопротивления R (рисунок 2.11 в).