3.1.3.2 Индуктивный элемент

Индуктивный элемент схемы замещения характеризует наличие изменяющегося магнитного поля, созданного током, протекающим в цепи. В цепях переменного тока, всякое изменение тока в проводнике сопровождается изменением потокосцепления _L этого проводника, что вызывает появление ЭДС самоиндукции в этом элементе е_L. Это явление получило название самоиндукции. ЭДС самоиндукции определяется скоростью изменения собственного потокосцепления:

.

Величина собственного потокосцепления индуктивного элемента пропорциональна величине тока в нем , где L – собственная индуктивность элемента. Когда магнитное поле образуется в немагнитной среде, зависимость является линейной и индуктивность элемента . Для катушек индуктивности с магнитным сердечником индуктивность зависит от протекающего тока. Условные графические обозначения катушек индуктивности без сердечника и с ферромагнитным сердечником приведены на рисунке 3.4 а, б.

Направление ЭДС самоиндукции определяется знаком производной тока по времени. При увеличении тока, ЭДС самоиндукции направлена встречно по отношению к направлению протекания тока и вычитается из приложенного напряжения (препятствует увеличению тока). При уменьшении тока направление ЭДС самоиндукции совпадает с направлением тока, ЭДС самоиндукции складывается с приложенным напряжением (стремится поддержать ток постоянным).

При синусоидальном токе в индуктивном элементе , по закону электромагнитной индукции напряжение на индуктивном элементе равно:

,

где амплитуды напряжения и тока связаны соотношением , действующие значения тока и напряжения соответственно , а их начальные фазы - . Величина называется индуктивным сопротивлением, единица ее измерения – [Ом]. Комплексные значения синусоидального тока и напряжения индуктивного элемента:

и .

Закон Ома в комплексной форме для индуктивного элемента:

или

График мгновенных значений напряжения и тока на индуктивном элементе показан на рисунке 3.6, а. Соответствующая векторная диаграмма приведена на рисунке 3.6 б, из которой видно, что вектор тока отстает от вектора напряжения на угол /2.

Рисунок 3.6 - График изменения мгновенных значений (а) и векторная диаграмма (б) тока и напряжения на индуктивном элементе

3.1.3.3 Емкостной элемент

Емкость учитывает изменение энергии электрического поля. Напряжение и ток емкостного элемента связаны уравнением:

.

Если напряжение на емкостном элементе u_C возрастает, то ток положителен. То есть в данный момент времени ток имеет направление, совпадающее с условно положительным направлением напряжения u_C. Заряд и энергия электрического поля между обкладками конденсатора

,

при этом возрастают. Энергия от источника передается электрическому полю. Когда напряжение u_C убывает, уменьшается и заряд, энергия запасенная в электрическом поле возвращается обратно в источник. Следовательно, емкостной элемент схемы замещения отражает обмен энергией между источником и электрическим полем. Обозначение емкостного элемента приведено на рисунке 2.4, в.

Если напряжение между выводами емкостного элемента изменяется синусоидально:

,

то ток через емкостной элемент:

,

где амплитуды напряжения и тока связаны соотношением

,

действующие значения тока и напряжения соответственно

,

а их начальные фазы

.

Величина называется емкостным сопротивлением, единица ее измерения – [Ом]. Комплексные значения синусоидального тока и напряжения емкостного элемента:

и .

Закон Ома в комплексной форме для емкостного элемента:

График мгновенных значений напряжения и тока на емкостном элементе показан на рисунке 3.7 а. Соответствующая векторная диаграмма приведена на рисунке 3.7 б, из которой видно, что вектор напряжения отстает от вектора тока на угол /2.

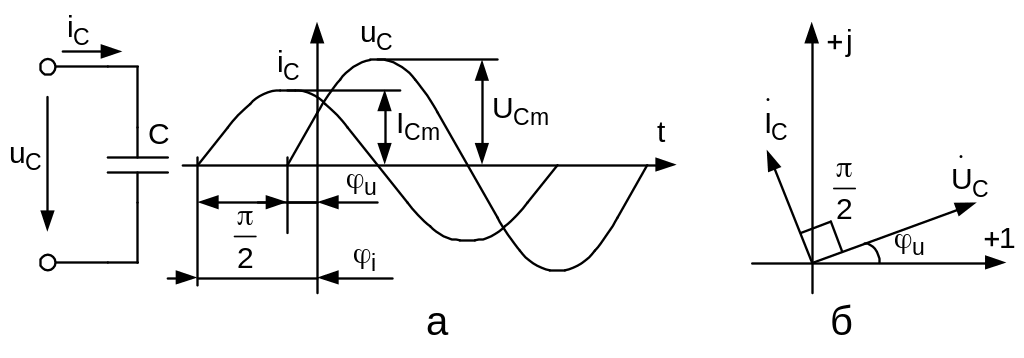
Рисунок 3.7 - График изменения мгновенных значений (а) и векторная диаграмма (б) тока и напряжения на емкостном элементе