2.4 Контрольные вопросы к лабораторной работе № 1

1. Что понимается под ветвью, узлом, контуром электрической схемы?

2. В чем отличие между принципиальной схемой и схемой замещения?

3. Сформулируйте закон Ома для участка цепи.

4. Как определяется эквивалентное сопротивление при последовательном, параллельном и смешанном соединении резисторов?

5. В чем заключается метод эквивалентных преобразований?

6. Сформулируйте и поясните первый и второй законы Кирхгофа.

3.Лабораторная работа №2 Электрические цепи однофазного переменного тока

Цель работы: Изучение основных законов и методов расчета линейных электрических цепей однофазного переменного тока.

3.1 Теоретическое введение

Основными преимуществами переменного синусоидального тока, обуславливающими его широкое распространение, являются возможность передачи энергии на дальние расстояния с малыми потерями, а так же простое преобразование электрической энергии с помощью трансформаторов. В настоящее время для большинства электрических сетей принята частота синусоидального тока 50 Гц – общепромышленная частота (в США и Японии – 60 Гц). Однако в различных отраслях промышленности встречаются другие стандарты частоты. Например, в электротермических установках используют диапазон частот 500 Гц – 50 кГц.

3.1.1 Максимальное, действующее и среднее значения синусоидальных величин

В линейной электрической цепи при действии синусоидально изменяющейся напряжения токи также имеют форму синусоиды (рисунке 3.1):

,

где - угловая частота, - частота переменного тока,  - начальная фаза, I_m , – максимальные значения (амплитуда) тока, напряжения.

Средним значением синусоидальной величины считают ее среднее значение за положительный полупериод или среднее значение по модулю за период. Например, для тока, приняв начальную фазу равной нулю, получим:

.

Синусоидальный ток, протекающий в резистивном элементе с сопротивлением r, вызывает нагрев этого элемента из-за выделения тепловой энергии. Такую же тепловую энергию в этом же резистивном элементе можно получить при протекании через него некоторой величины постоянного тока. Величина этого постоянного тока равна действующему значению соответствующего синусоидального тока. Действующее значение синусоидального тока определяется по формуле:

.

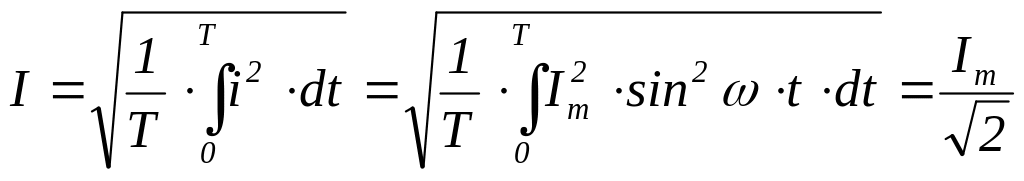Аналогично, для любой другой синусоидальной величины:

,

(ЭДС, напряжение и т.д.) среднее и действующее значения определяются из выражений:

,

.

3.1.2 Способы представления синусоидальных величин

Известно несколько способов представления синусоидальных величин: в виде тригонометрических функций, в виде графиков, в виде вращающихся векторов и виде комплексных чисел. Представление синусоидальных величин в виде тригонометрических функций рассматривалось выше ( ), пример представления синусоидальных величин в виде графиков показан на рисунке 3.1.

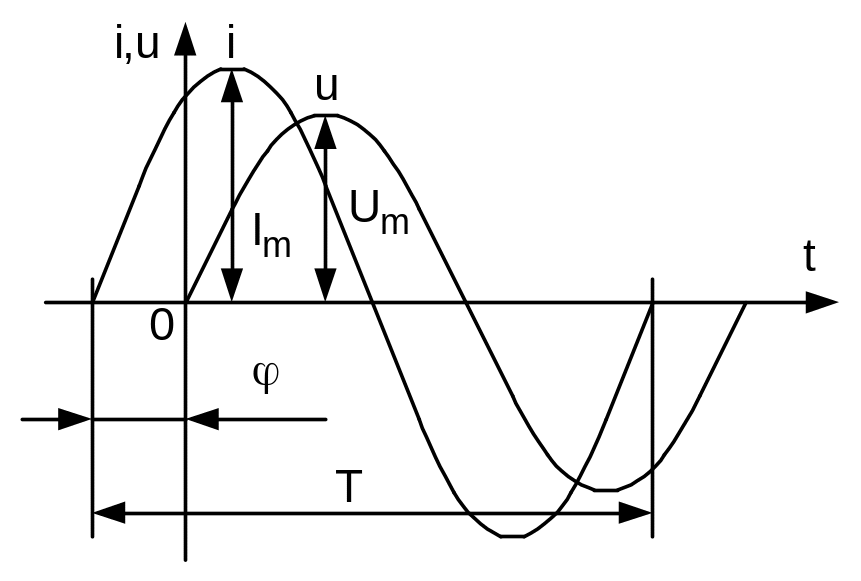
Рисунок 3.1 - Форма синусоидального тока

3.1.2.1 Представление синусоидальных величин вращающимися векторами

Для представления синусоидально изменяющейся величины , график изменения во времени, которой показан на рисунке 3.2, построим радиус-вектор этой величины , для моментов времени , t₁ - t₆. Длина этого вектора равна амплитуде синусоидальной величины . В момент времени , угол наклона вектора к горизонтальной оси равен . В моменты времени t₁ - t₆, радиус вектор будет поворачиваться против часовой стрелки на угол . При этом его проекция на вертикальную ось будет равна . Таким образом, синусоидально изменяющуюся величину можно представить в виде вектора, вращающегося с постоянной угловой скорость , и имеющего длину равную амплитудному значению синусоидальной величины.

Рисунок 3.2 - Представление синусоидальной величины вращающимся вектором

Применение вращающихся векторов позволяет компактно представить на одном рисунке несколько различных величин изменяющихся с одной частотой, так как их положение (угол сдвига) друг относительно друга остается неизменным. Совокупность векторов нескольких синусоидальных величин одной частоты называют векторной диаграммой. Пользуясь векторной диаграммой, сложение и вычитание мгновенных значений можно заменить сложением и вычитанием соответствующих векторов.