2.2 Ориентированный объем параллелепипеда, построенного на векторах , и

Пусть , и – некоторые некомпланарные векторы общего положения, рассмотрим наиболее простые частные случаи, когда векторы , и расположены вдоль координатных осей рис. 2.2

Рисунок 2.2 - Частный случай расположения векторов

Наши дальнейшие рассуждения будут опираться на простой геометрический факт [1,2]: объем параллелепипеда не изменится, если любую его грань произвольно переместить в своей плоскости параллельно самой себе рис. 2.3

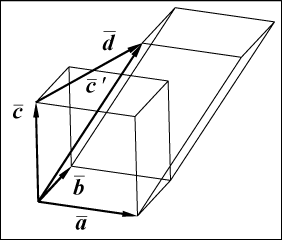
Рисунок 2.3 - Параллелепипед с параллельно смещенной гранью

Теперь после всех этих замечаний перейдем непосредственно к нашей задаче.

Отложим векторы , и от начала координат.

На рис. 2.4 сплошными линиями показан параллелепипед, построенный на этих векторах.

Рисунок 2.4 - Параллелепипед построенный на векторах , и

Теперь выполним следующие элементарные преобразования параллелепипеда, не приводящие к изменению объема и ориентации [1,3].

Результаты приведены в таб. 2.1

Таблица 2.1 – Результаты основных и элементарных преобразований параллелепипеда не приводящих к изменению объема и ориентации

Шаг 1	Шаг 2	Шаг 3	Шаг 4	Шаг 5	Шаг 6
4	78	98	90	65	65
4	43	587	78	34	45
3	54	423	678	67	656
3	35	43	787	98	653
3	23	5443	786	87	356
44	32	43	56	76	546
34	31	432	67	76	56

3 Описание алгоритма решения задачи

Программа должна обеспечивать два режима работы при вычислении значений функции:

1. Точечный просчет. Должна быть обеспечена возможность установки значения для любого параметра функции, после чего рассчитывается и отображается значение функции.

2. Просчет в диапазонном режиме. Один из параметров должен изменяться в любом допустимом диапазоне значений для задаваемого количества точек. При этих условиях выполняется расчет и отображение значений аргумента и соответствующих им значений функции при заданных значениях остальных параметров.

3.1 Описание алгоритма программы

По условиям, заданным в задаче, значение внутреннего радиуса цилиндрической трубы R1 изменяется сo значения L до N с шагом M.

Следовательно, необходимо перебирать результаты вычисления объёма цилиндрической трубы с каждым изменением внутреннего радиуса основания, до тех пор, пока объём цилиндрической трубы не станет больше или равен объёму прямоугольного параллелепипеда.

В соответствии с приведённым словесным описанием алгоритма решения поставленной задачи разработана схема решаемой задачи

В изображенном алгоритме блоки имеют описанное ниже назначение:

Блок 1. Начало программы;

Блок 2. Ввод L,N,M,R2,H,A,B,C с клавиатуры;

Блок 3. Вычисление объёма прямоугольного параллелепипеда;

Блок 4. Установка начального максимального значения внутреннего радиуса цилиндрической трубы;

Блок 5. Организация цикла переменной R1;

Блок 6. Вычисление объёма цилиндрической трубы;

Блок 7. Проверка условия Vc <= Vt, если оно выполняется, то переход на блок 8, если нет, то на блок 10;

Блок 8. Проверка условия MAX < R1, если оно выполняется, то переход на блок 9, если нет, то на блок 10;

Блок 9. Вычисление максимального значения внутреннего радиуса, объёма цилиндрической трубы;

Блок 10. Вывод значений объёма цилиндрической трубы, объёма прямоугольного параллелепипеда, максимального значения внутреннего радиуса;

Блок 11. Конец программы.

Реализация алгоритма приведена в программе см. приложение А.