8 Задачі математичної фізики

8.1 Класифікація рівнянь математичної фізики

При вивченні більшості фізичних явищ та процесів приходиться мати справу з тим, що їх властивості описуються диференціальними рівняннями у часткових похідних, в яких невідомими величини є функції не однієї, а декількох змінних. Аргументам таких рівнянь надають змісту просторових змінних або просторових змінних і часу.

В загальному випадку диференціальне рівняння з частковими похідними можна записати у такій формі:

(8.1)

де - постійні коефіцієнти,

- невідома функція, аргументи якої змінні і , одна із яких може бути часом , а інша, допустимо , просторовою змінною;

; ; - часткові похідні другого порядку;

; - часткові похідні першого порядку;

- відома функція, яка враховує взаємодію фізичної системи з навколишнім середовищем.

Існує три типи рівнянь (8.1).

Якщо , то рівняння (8.1) називається еліптичним;

Якщо , то рівняння (8.1) буде параболічним і якщо , то матимемо гіперболічне рівняння.

У випадку постійних коефіцієнтів при похідних другого порядку шляхом перетворення змінних рівняння (8.1) можна привести до виду, яке не вміщує змішаних похідних (b = 0). Тоді тип рівняння визначається за таким правилом: якщо у рівняння (8.1) b = 0 і постійні коефіцієнти при похідних другого порядку мають одинакові знаки в одній частині рівняння, то таке рівняння – еліптичне; якщо різні – гіперболічне; якщо похідна другого порядку за однією із змінних відсутня (b = 0; ас = 0 при ) – параболічне.

8.2 Еліптичні рівняння

Як приклади еліптичних рівнянь у часткових похідних можна навести рівняння Лапласа, Пуассона і Гельмгольца.

Якщо ввести оператор Лапласа функції , то в загальному вигляді можна записати

- рівняння Лапласа;

- рівняння Пуассона;

- рівняння Гельмгольца,

де , - задані функції, зміст яких визначається задачею, що розв’язується.

У рівняннях Лапласа, Пуасона, Гельмгольца одна із змінних може бути як просторовою координатою, так і часом .

Рівняння Лапласа використовують для математичного опису електромагнітних полів, магнітних полів постійного струму, стаціонарних теплових полів.

Області застосування рівнянь Пуассона – задачі електростатики, електронної оптики, теорії пружності та ін.

Рівняння Гельмгольца є математичною моделлю коливних процесів, наприклад, в акустиці.

Допустимо, що розв’язок еліптичного рівняння належить області Ω з границею Г. Розглянемо найпростіший випадок, коли Ω - прямокутник [a, b] x [c, d].

Двовимірну область  накриємо сіткою вузлів з координатами (рис 8.1), де , ; , , ,

- кількість вузлів розбиття ; - кроки та сітці.

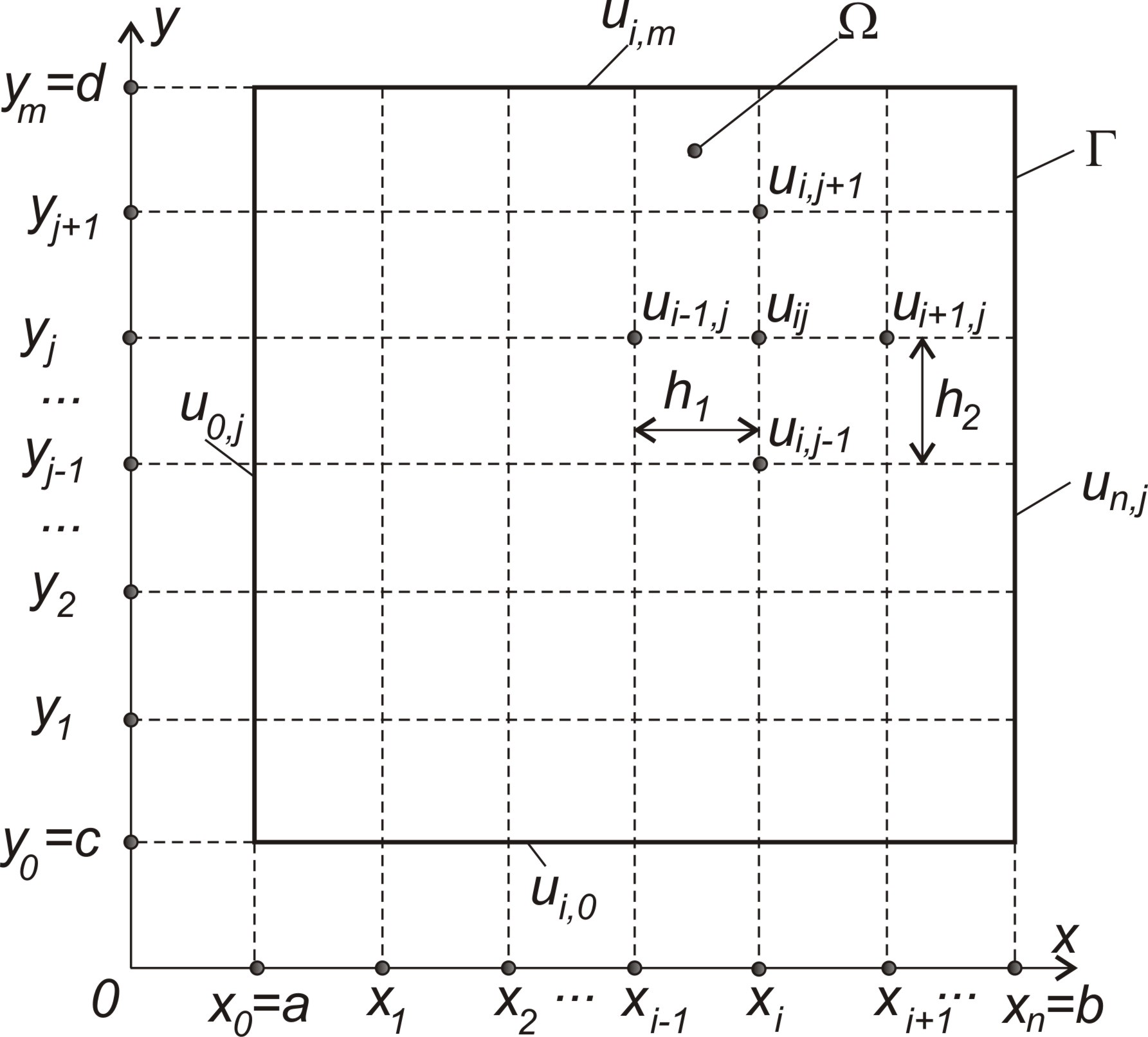
Рисунок 8.1 –Сітка для дискретизації задачі

Вузли називають внутрішніми, коли , і граничними, коли або та або , тобто , ,

, (8.2)

, , .

Виразимо оператор Лапласа у дискретному вигляді, скориставшись формулою для обчислення наближення до другої похідної

. (8.3)

Відповідно до формули (8.3) будемо мати

(8.4)

і відповідно

. (8.5)

Якщо - розрахункова точка, то і відповідно , , , ,

де .

Аналогічно , ,

Отже, в розрахунковій точці часткові похідні і можна замінити такими різницевими рівняннями :

,

.

Переходячи до прийнятих позначень, отримаємо

, (8.6)

. (8.7)

Таким чином,

. (8.8)

Різницеве рівняння (8.8) можна спростити, якщо крок сітки зробити постійним як за змінною , так за змінною тобто .

Тоді

. (8.9)

Допустимо, що числовим методом необхідно розв’язати диференціальне рівняння з частковими похідними другого порядку, яке є еліптичним рівнянням

, (8.10)

де - задана функція, а  - прямокутник. Тоді у відповідності з (8.8) запишемо дискретний аналог еліптичного рівняння

. (8.11)

Рівняння (8.10 необхідно доповнити сукупністю граничних умов (8.2 ) на Г.

Розглянемо техніку обчислення значень функції у вузлах решітки  Розглянемо перших три шари решітки (рис 8.2). Зафіксуємо значення j. Візьмемо j = 1.

Тоді при із (8.11) отримаємо рівняння

.

Якщо тепер змінювати від 2 до , то

, .

І, нарешті, при будемо мати

,

де .

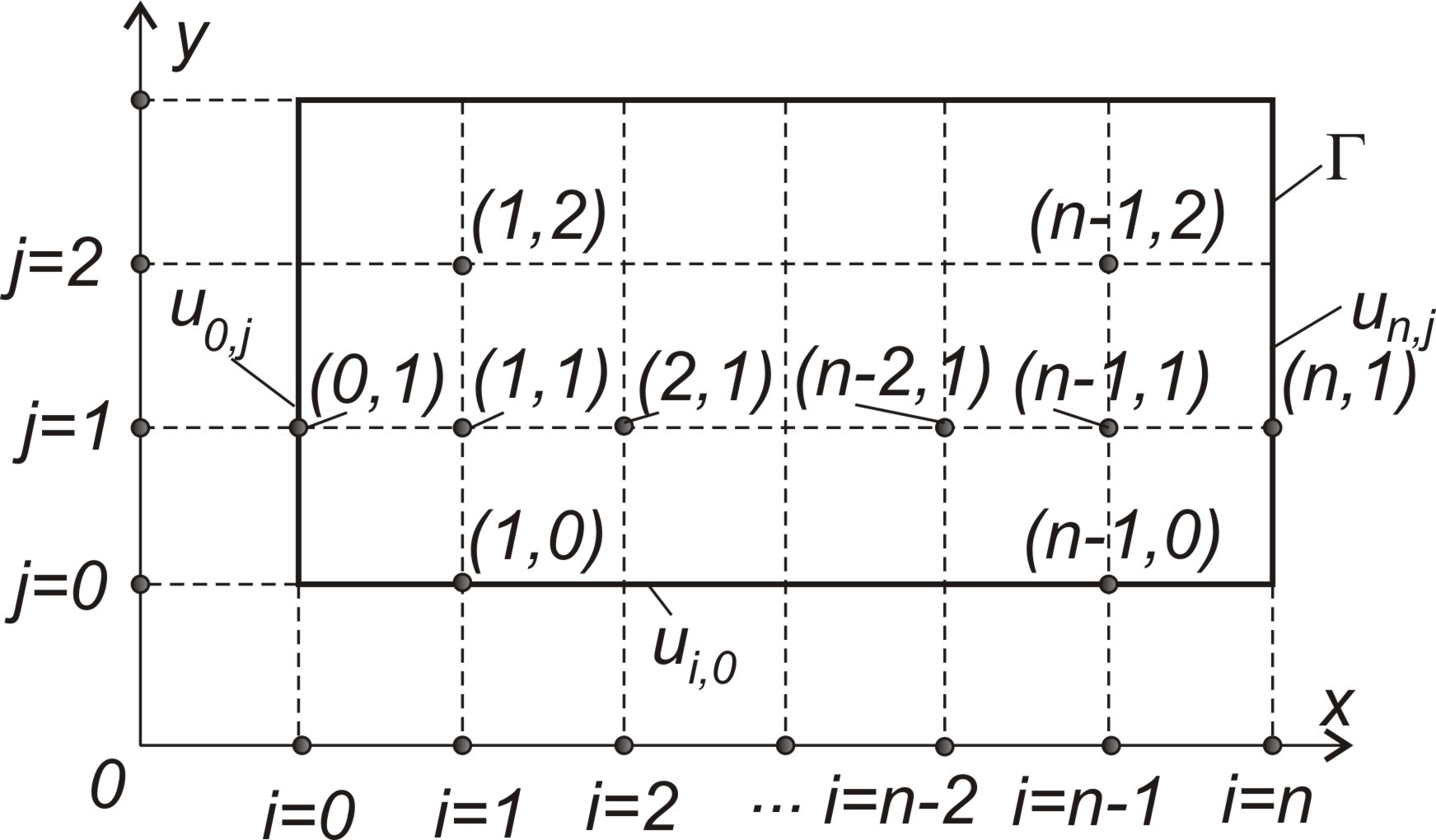
Рисунок 8.2-Перші три шари решітки 

Тепер можна взяти j = 2 і знову скласти систему із n-1 рівнянь. Повторюючи процес складання рівнянь для , отримаємо систему із рівнянь в якій невідомих.

Сказане проілюструємо конкретним прикладом.

Приклад 8.1. Знайдемо наближений розв’язок еліптичного рівняння у прямокутнику де - температура у точці (x,y), а граничні умови наступні :

для ,

для .

Виберемо крок сітки знайдемо кількість вузлів сітки: в напрямку ; у напрямку .

Сітка  показана на рис 8.3

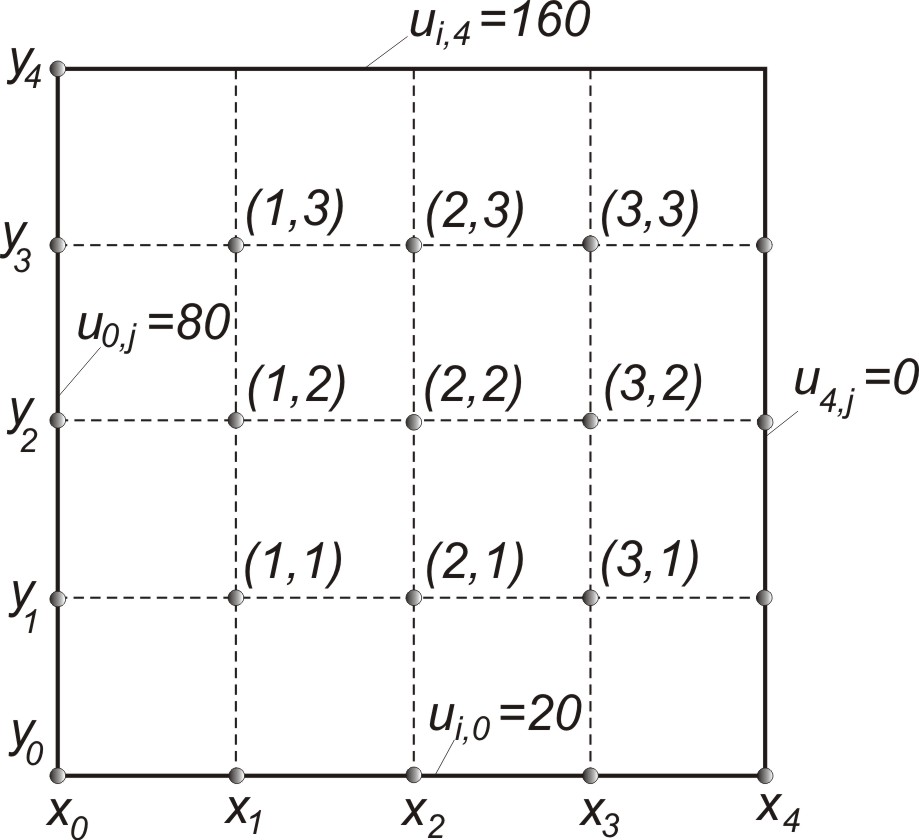
Рисунок 8.3 – Сітка  для n=m=5

Складемо систему алгебраїчних рівнянь використавши формулу (8.11) в якій , а . Маємо

. (8.12)

Змінюючи індекси та j від 1 до 3 отримаємо систему із дев’яти рівнянь

,

,

;

,

,

,

;

,

,

.

Отриману систему рівнянь можна записати у матрично векторній формі

, (8.13)

де

, ,

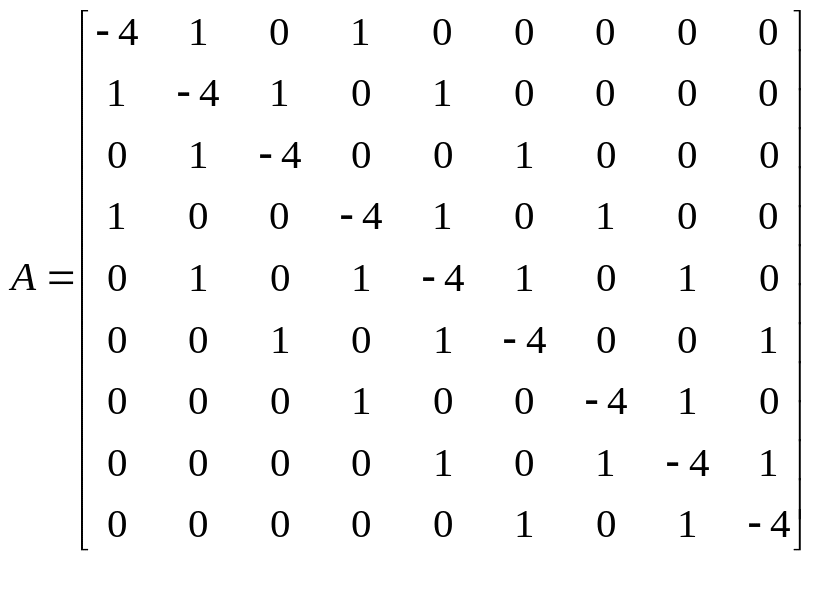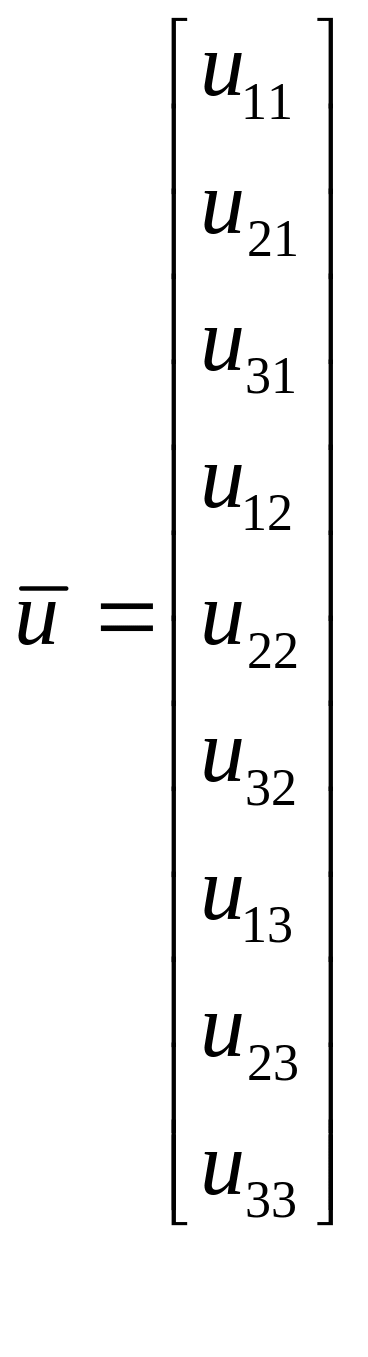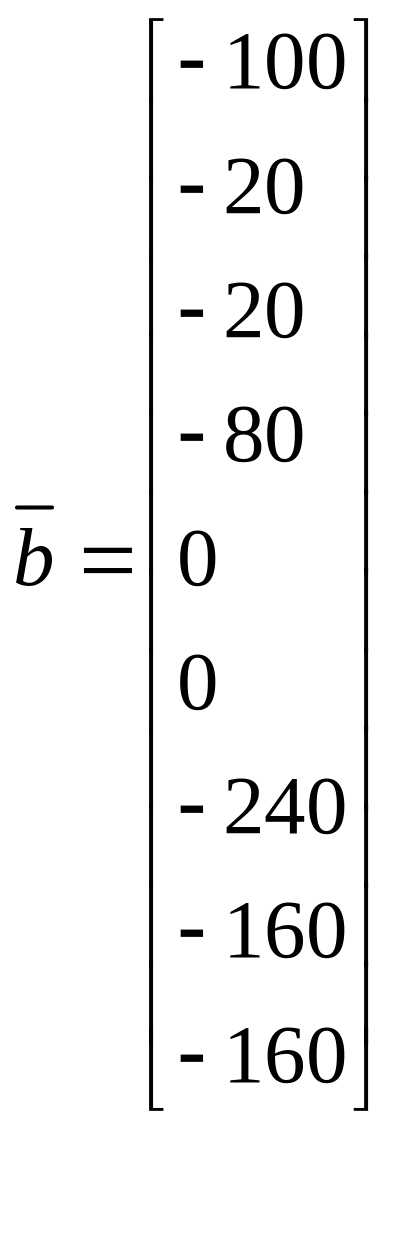
Відмітимо, що при складанні системи рівнянь зручно використовувати шаблон типу “хрест” (рис 8.4) . Першою у рівнянні (8.11) записується змінна другою , третьою з коефіцієнтом мінус чотири, четвертю і п’ятою .

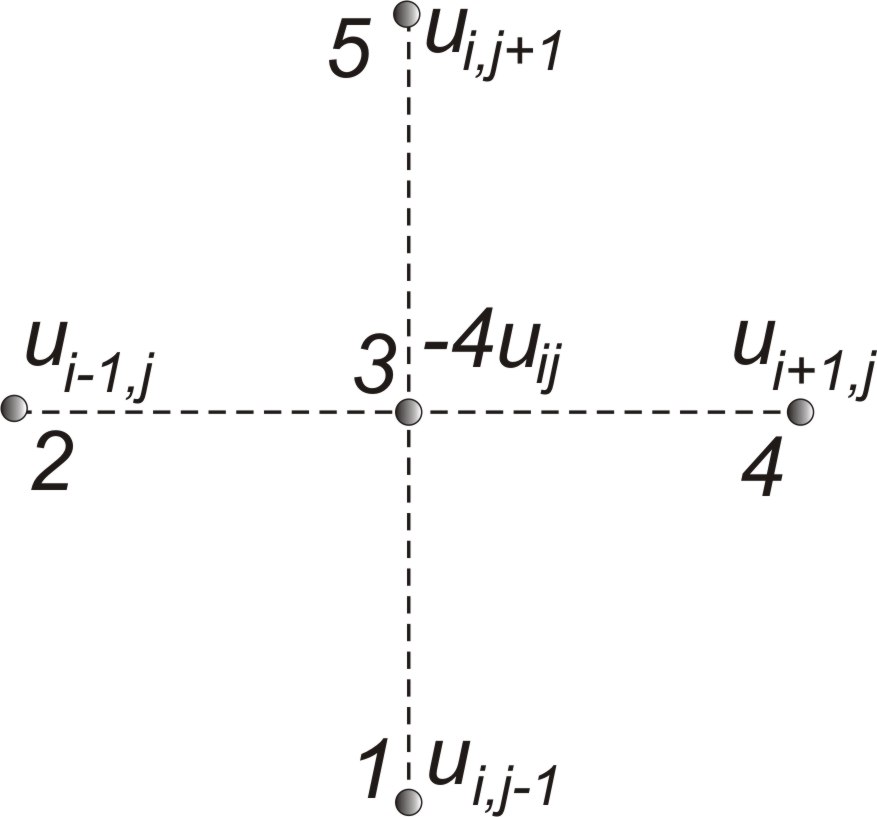
Рисунок 8.4-Шаблон типу “хрест”

У тому випадку, коли у процесі складання рівнянь шаблон вміщує граничні точки, то значення відповідних змінних та , які відповідають таким точкам, переносяться у праву частину рівнянь (8.11).

Для розв’язування отриманої системи рівнянь (8.13) скористаємося процедурою SystemEqualizationAgebra (роділ 6). У результаті розв’язку отримані такі значення компонентів вектора: Графік зміни температурного поля в координатах показаний на рис 8.5.

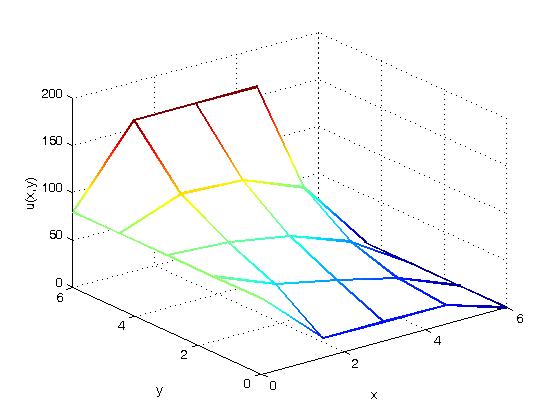
Рисунок 8.5 –Графік зміни температури у вузлових