Лемма о несамодвойственной функции

Подстановкой функций и в несамодвойственную функцию можно получить одну из констант.

Доказательство. Пусть – несамодвойственная функция. Тогда существует набор , для которого . Построим функцию , заменив единицы в на , а нули – на . Так как , то . Заметим, что .

Тогда , т.е. . Следовательно, функция есть одна из констант.

2.4.4 Разложение булевой функции по переменным

Обозначим x^=

Посмотрим, чему равно x^ при разных значениях x и .

x\	0	1
0	1	0
1	0	1

Из таблицы следует: x^=1 тогда и только тогда, когда x=.

Теорема о разложении функции по переменным

П усть f(x₁, ..., x_n) P₂. Тогда для любого m: 1 ≤ m ≤ n допустимо представление:

f(x₁, ..., x_m, x_m+1, ..., x_n) = ,

где дизъюнкция берется по всем наборам из 0 и 1. Это представление называется разложением функции f по переменным x₁, ..., x_n.

Прежде чем доказать утверждение, рассмотрим примеры.

Пример 1. m = 1, запишем разложение по переменным х:

f(x₁, ..., x_n) = = f(0, x₂ , …,x_n)x₁f(1, x₂, ..., x_n). (1)

Пример 2. m=2, запишем разложение по переменным х и :

f(x₁,x₂,…x_n) = =

.

Если f(x_, x_) = x_x_, то последняя формула дает x_x_= x_x_ .

Доказательство. Для доказательства возьмем произвольный набор _,,_n) и покажем, что левая и правая части формулы (1) принимают на этом наборе одинаковые значения. Слева имеем f_ ._n. Cправа : .

Дизъюнкция берется по всевозможным наборам (_, ..., _m). Если в этих наборах хотя бы одно _i  _i (1≤i≤m), то = 0 и , следовательно, ненулевой член будет только на наборе (_, ..., _m) = (_, ..., _m), тогда f_ ._n.

Следствие 1. Любую функцию f(x₁, ..., x_n) не равную тождественно нулю можно представить в виде: , причём единственным образом. Этот вид называется совершенной дизъюнктивной нормальной формой функции f(x₁, ..., x_n) и записывается СДНФ.

Доказательство. Существование СДНФ для функции не равной тождественно нулю вытекает из предыдущей теоремы. Покажем, что эта СДНФ единственная. В самом деле, имеется n-местных функций, не равных нулю тождественно. Подсчитаем число различных СДНФ от n переменных. Путь означает число сочетаний из n элементов по k. Тогда число одночленных СДНФ равно . Число k-членных СДНФ равно . Число n-членных СДНФ равно . Число всех различных СДНФ

Итак, функций реализуются посредством СДНФ, т.е. каждой функции соответствует единственная СДНФ.

Замечание. – элементарная конъюнкция ранга n по числу входящих переменных, предполагается, что при i  j , х_i  х_j. СДНФ для f(x₁, ..., x_n) –дизъюнкция элементарных конъюнкций ранга n. Если функция представлена в виде дизъюнкций элементарных конъюнкций, где ранг хотя бы одной элементарной конъюнкции меньше n, то такая форма называется дизъюнктивной нормальной формой (ДНФ).

Cледствие 2. Любая функция алгебры логики может быть представлена в виде формулы через отрицание, & и .

а) Если f ≡ 0, то f(x₁, ..., x_n) = & .

б) Если f(x₁, ..., x_n)  0 тождественно, тогда ее можно представить в виде СДНФ, где используются только связки , &, . СДНФ дает алгоритм представления функции в виде формулы через &, , .

Пример 3. Пусть функция f(x₁, x₂, x₃) задана таблицей истинности. Запишем ее в виде СДНФ. Наборов, на которых функция равна 1, три: (0, 1, 0), (1, 0, 0) и

(1, 1, 1), поэтому f(x₁, x₂, x₃) = x₁⁰ & x₂¹ & x₃⁰ x₁¹ & x₂⁰ & x₃⁰ x₁¹&x₂¹ & x₃¹=

_{= &x2& x1& & x1&x2&x}3.

x1	x2		x3		f
0 0 0 0 1 1 1 1		0 1 1 1 0 0 1 1		0 1 0 1 0 1 0 1		0 0 1 0 1 0 0 1

С ледствие 3. Мы умеем представлять функцию в виде . Нельзя ли представить ее в виде . Пусть функция f(x₁, ..., x_n) 1 тождественно. Тогда функция f* 0 тождественно, и ее можно представить в виде СДНФ:

.

По принципу двойственности заменим & на и наоборот, получим

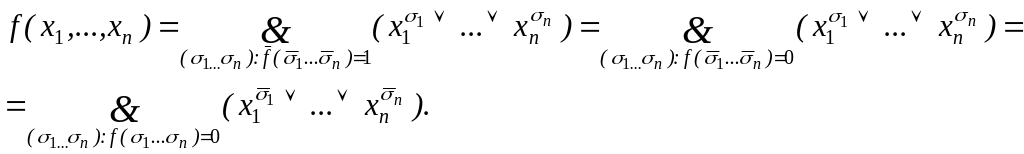(2)

называется элементарной дизъюнкцией ранга n. Представление функции в виде (2) называется совершенной конъюнктивной нормальной формой или в краткой записи – СКНФ. СКНФ для f(x₁, ..., x_n) – конъюнкция элементарных дизъюнкций ранга n. КНФ для f(x₁, ..., x_n) – конъюнкция элементарных дизъюнкций, где ранг хотя бы одной элементарной дизъюнкции меньше n.

Пример 4. Пусть f(x₁, x₂, x₃) = x₁ (x₂ (x₃ ~ x₁)). Представим ее в виде СКНФ, для этого получим таблицу истинности.

x1	x2	x3	x3~x1	x 2 (x3~x1)	f
0 0 0 0 1 1 1 1	0 0 1 1 0 0 1 1	0 1 0 1 0 1 0 1	1 0 1 0 0 1 0 1	1 1 1 0 1 1 0 1	1 1 1 1 1 1 0 1

Функция равна нулю только на наборе (1, 1, 0), поэтому

f(x₁ x₂ x₃)=x₁ x₂ x₃ =x₁⁰x₂⁰x₃¹=   x₃.