20

Лекция 1

Условные обозначения

def – определение

 – включает (подмножество)

 - надмножество

 - объединение множеств

 - пересечение множеств

 - пустое множество

 - бесконечность

 - принадлежит (элемент множеству)

 - следует, выполняется

 - тогда и только тогда

 - любой

 - существует

] – пусть

! – единственный

~ - эквивалентно

N - натуральные числа

Z -целые числа

Q - рациональные числа.

R - действительные числа.

Понятие последовательности

 Если функция определена на множестве натуральных чисел N, то такая функция называется бесконечной числовой последовательностью. Обычно числовые последовательность обозначают как(X_n), где n принадлежит множеству натуральных чисел N. Если функция определена на конечном подмножестве N : n=1, 2, ... k , то это конечная числовая последовательность.

Числовая последовательность может быть задана формулой, таблицей, графиком и с помощью рекуррентных соотношений. Например, X_n=1/(2*n). Таким образом мы ставим в соответствие каждому натуральному числу n некоторый определенный элемент последовательности (X_n).

Если теперь последовательно брать n равными 1,2,3, …., мы получим последовательность (X_n): ½, ¼, 1/6, …, 1/(2*n), …  

Виды последовательности

Последовательность (бесконечная)может быть ограниченной или неограниченной, возрастающей или убывающей.

Последовательность (X_n) называет ограниченной, если существуют два числа m и M такие, что для любого n принадлежащего множеству натуральных чисел, будет выполняться равенство m<=X_n

Последовательность (X_n), не являющаяся ограниченной, называется неограниченной последовательностью.

Последовательность (X_n) называется возрастающей, если для всех натуральных n выполняется следующее равенство X_n+1 > X_n. Другими словами, каждый член последовательности, начиная со второго, должен быть больше предыдущего члена.

Последовательность (Xn) называется убывающей, если для всех натуральных n выполняется следующее равенство X_n+1 < X_n. Иначе говоря, каждый член последовательности, начиная со второго, должен быть меньше предыдущего члена.

Прогрессии      Арифметическая прогрессия

     Арифметическая прогрессия - числовая последовательность определяемая условиями: 1) 2) (d - разность арифметической прогрессии).

     Свойства арифметической прогрессии:

     Формула n-го члена:

     Формулы суммы n первых членов:

     Геометрическая прогрессия

     Геометрическая прогрессия - числовая последовательность определяемая условиями: 1) 2) n = 1, 2, ... (q - знаменатель геометрической прогрессии).

     Свойства геометрической прогрессии:

     Формула n-го члена:

     Формулы суммы n первых членов :

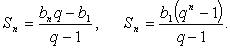
     Сумма бесконечной геометрической прогрессии:

Рекуррентные соотношения

Рекуррентные соотношения - соотношения вида "следующий через предыдущих", то есть отношение, когда значение f(n) описывается через f(m), где n > m. f - функция целого аргумента, обычно натурального или целого неотрицательного.

В общем случае рекуррентное соотношение записывается в виде g(n) = f(n, g(n-1), g(n-2), ..., g(n-k)), где k - порядок рекуррентного соотношения. ИНАЧЕ: Рекуррентное соотношение имеет порядок k, если оно позволяет выразить f(n+k) через f(n), f(n+1), …, f(n+k-1). Если задано рекуррентное соотношение k-го порядка, то ему могут удовлетворять бесконечно много последовательностей, так как первые k элементов последовательности можно задать произвольно – между ними нет никаких соотношений. Но если первые k членов заданы, то все остальные элементы определяются однозначно. Должны быть известны некоторые начальные условия, за счёт которых вычисление значения f будет однозначным. Для рекуррентного соотношения порядка k должны быть хотя бы k начальных условий вида g(x)=y, где x, y известны, например, известны значения g(0), g(1), ..., g(k-1). Пример: i-ый член арифметической прогрессии может определяться как a(i) = a(i - 1) + d. В качестве начального условия выступает первый член прогрессии, а порядок k = 1.

f(n+2)=f(n)f(n+1)-3f²(n+1)+1 – рекуррентное соотношение второго порядка.

f(n+3)=6f(n)f(n+2)+f(n+1) – рекуррентное соотношение третьего порядка.

Пользуясь рекуррентным соотношением и начальными членами, можно один за другим выписывать члены последовательности, при этом рано или поздно мы получим любой её член. Однако если необходимо узнать только один определенный член последовательности, то нерационально вычислять все предыдущие. В этом случае удобнее иметь формулу для вычисления n-го члена.

Как получить рекуррентные соотношения для рядов

Иногда задание n-го члена ряда как функции от n неудобно. Например, эта ситуация имеет место, когда требуется найти сумму первых k членов ряда, при этом формула для n-го члена содержит степени, факториалы. В случаях вроде только что названного поступают так: первый член ряда берут как начальное условие. Составляют формулу вида g(n) = a(n+1)/a(n). Далее равенство a(n+1) = a(n) * g(n) берут как рекуррентное соотношение.

Числа Фибоначчи

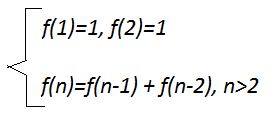
Эта формула определяет так называемые числа Фибоначчи (0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, …Название по имени средневекового математика Леонардо Пизанского (или Фибоначчи)), то есть последовательность натуральных чисел, где каждое число есть сумма двух предыдущих. Порядок данного рекуррентного соотношения равен 2, соответственно требуется два начальных условия. Иногда числа Фибоначчи рассматривают и для отрицательных номеров n как двусторонне бесконечную последовательность, удовлетворяющую тому же рекуррентному соотношению. При этом члены с отрицательными индексами легко получить с помощью эквивалентной формулы «назад»: :

n	−10	−9	−8	−7	−6	−5	−4	−3	−2	−1	0	1	2	3	4	5	6	7	8	9	10
	−55	34	−21	13	−8	5	−3	2	−1	1	0	1	1	2	3	5	8	13	21	34	55

Легко заметить, что .

Числа Катала́на

Числа Катала́на — числовая последовательность, встречающаяся во многих задачах комбинаторики. Последовательность названа в честь бельгийского математика Каталана, хотя была известна ещё Л. Эйлеру.

Первые несколько чисел Каталана:

1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190, 6564120420, 24466267020, 91482563640, 343059613650, 1289904147324, 4861946401452, …

n-е число Каталана можно определить одним из следующих способов:

• Количество разбиений выпуклого (n+2)-угольника на треугольники непересекающимися диагоналями.

• Количество правильных скобочных последовательностей длины 2n, то есть таких последовательностей из n левых и n правых скобок, в которых количество открывающих скобок равно количеству закрывающих, и в любом её префиксе открывающих скобок не меньше, чем закрывающих.

Например, для n=3 существует 5 таких последовательностей:

((())), ()(()), ()()(), (())(), (()())

то есть .

• Количество способов соединения 2n точек на окружности n непересекающимися хордами.

• Количество неизоморфных упорядоченных бинарных деревьев с корнем и n+1 листьями.