Государственное бюджетное образовательное учреждение
среднего профессионального образования
Павловский автомеханический техникум им. И.И. Лепсе
Задания
для расчетно-графических работ
по дисциплине
«Техническая механика»
для студентов специальностей
151901 «Технология машиностроения»
150412 «Обработка металлов давлением»
190103 «Автомобиле- и тракторостроение»
140448 «Техническая эксплуатация и обслуживание электрического и электромеханического оборудования»
151031 «Монтаж и техническая эксплуатация промышленного оборудования»
190631 «Техническое обслуживание и ремонт автомобильного транспорта»
Расчетно-графическая работа №1
по теме:
«Равновесие плоской системы сходящихся сил»
Последовательность решения задачи:
1. Выбрать тело (точку), равновесие которого следует рассматривать.
2. Освободить тело (точку) от связей и изобразить действующие на него активные силы и реакции отброшенных связей.
3. Выбрать оси координат и составить уравнения равновесия, используя условия равновесия системы сходящихся сил на плоскости:
ΣХi=0; ΣYi=0.
Начало координат совмещают с точкой, равновесие которой рассматривается. Выбирая оси координат, следует учитывать, что полученные уравнения будут решаться проще, если одну из осей направить так, чтобы она совпадала с направлением одной из неизвестных реакций, а другая при этом составляла бы с первой угол 900.
4. Определить реакции связей из решения указанной системы уравнений.
5. Проверить правильность полученных результатов. Обычно проверка делается графическим или другим способами, но может быть выполнена и аналитически. Для этого следует изменить положение осей координат и решить задачу в новой системе. Ответы должны быть одинаковыми.
Пример выполнения расчетно-графической работы.
6. Проверим решение, для чего расположим оси координат как показано на рисунке 2, д. Составим уравнения равновесия для вновь принятых осей:
1) ΣХ= -S1cos200-S2cos600=0;
2) ΣY= -G-S1cos700-S2cos300=0
Решим систему уравнений способом подстановки.
Из первого уравнения находим S1:
Подставим это выражение во второе уравнение:
откуда
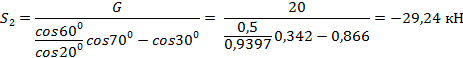
Теперь найдем S1:
Очевидно, что при расположении осей, как показано на рис. 2, д, вычисления оказались более сложными.
Ответ: S1= 15,56 кН; S2= -29, 24 кН (при принятом на чертеже направлении усилий).
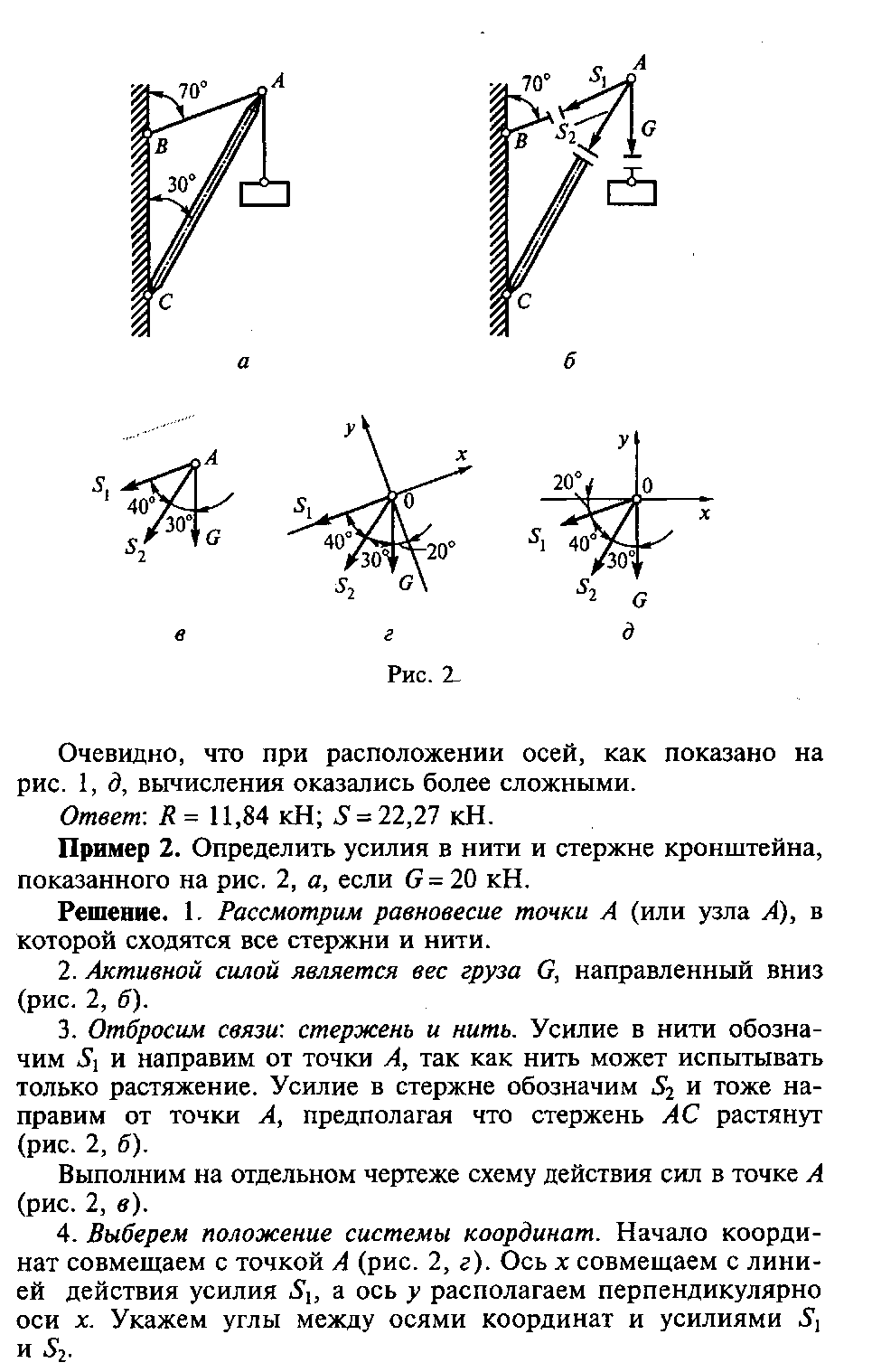
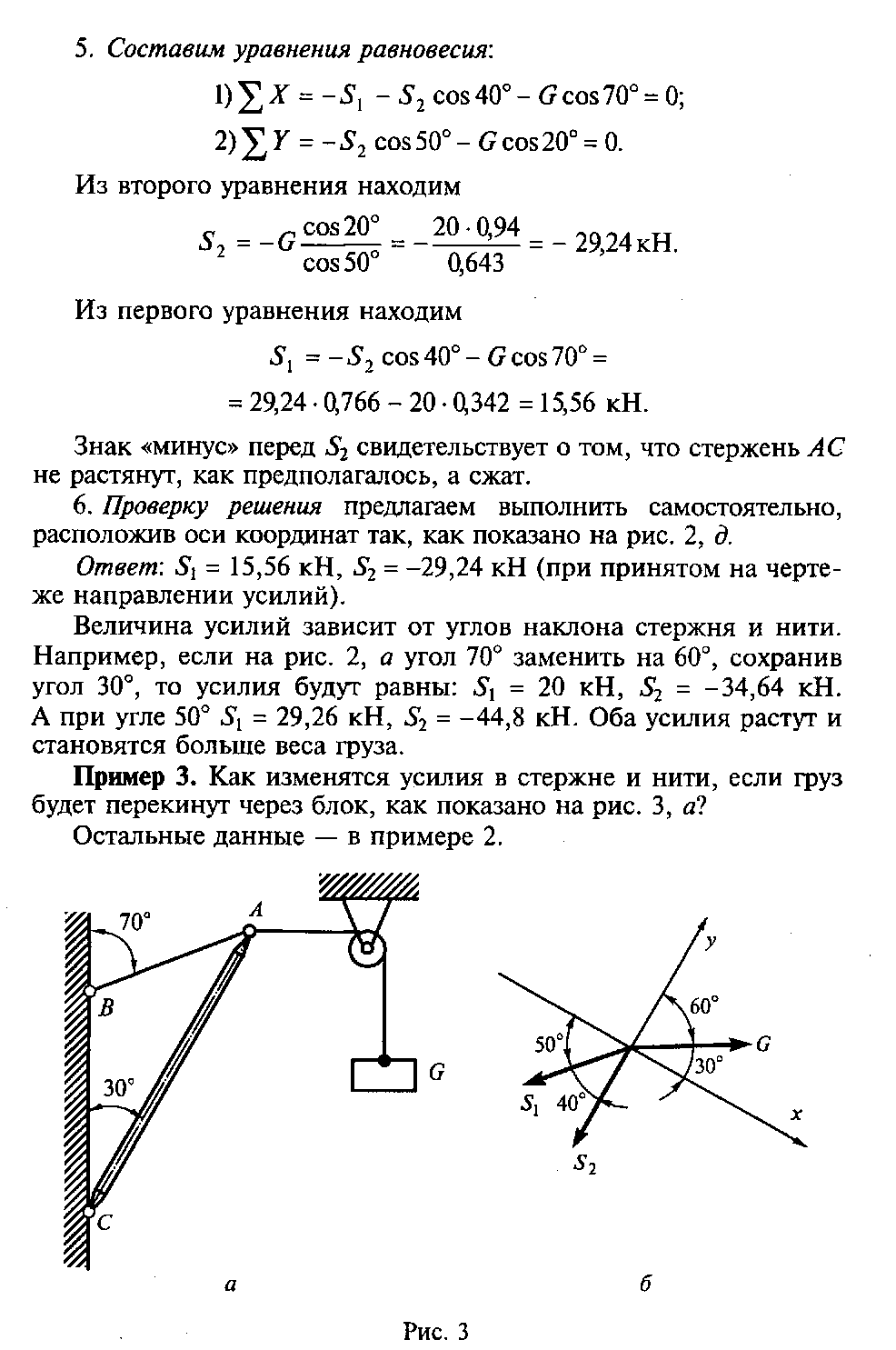
Пример 3. Определить усилия в нити и стержне кронштейна, показанного на рис. 3, а, если G=20 кН.
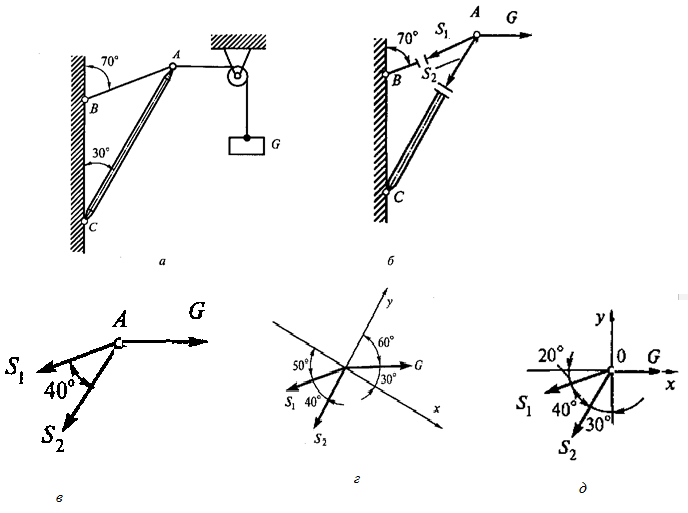
Рис. 3
Решение. 1. Рассмотрим равновесие точки А (или узла А), в которой сходятся все стержни и нити.
2. Активная сила (вес груза G) действует на точку горизонтально слева направо, так как груз перекинут через блок (рис. 3, б).
3. Отбросим связи: стержень и нить. Усилие в нити обозначим S1 и направим от точки А, так как нить может испытывать только растяжение. Усилие в стержне обозначим S2 и тоже направим от точки А, предполагая, что стержень АС растянут (рис.3, б).
Выполним на отдельном чертеже схему действия сил в точке А (рис. 3, в).
4. Выберем положение системы координат. Начало координат совмещаем с точкой А. ось y совмещаем с линией действия усилия S2, а ось х располагаем перпендикулярно оси y. Укажем углы между осями координат и усилиями S1 и S2 (рис. 3, г).
5. Составляем и решаем уравнения равновесия:
Знак «минус» перед S2 свидетельствует о том, что стержень АС не растянут, как предполагалось, а сжат.
6. Проверим решение, для чего расположим оси координат как показано на рисунке 2, д. Составим уравнения равновесия для вновь принятых осей:
1) ΣХ= G-S1cos200-S2cos600=0;
2) ΣY= -S1cos700-S2cos300=0
Решим систему уравнений способом подстановки.
Из второго уравнения находим S1:
Подставим это выражение во второе уравнение:
откуда
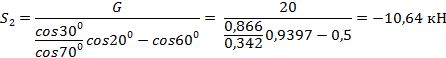
Теперь найдем S1:
Очевидно, что при расположении осей, как показано на рис. 2, д, вычисления оказались более сложными.
Ответ: S1= 26,94 кН; S2= -10,64 кН (при принятом на чертеже направлении усилий).
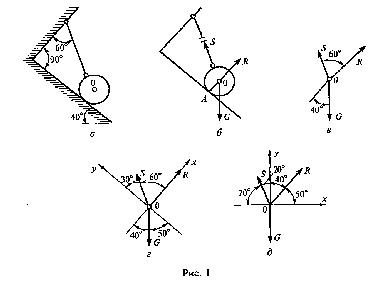
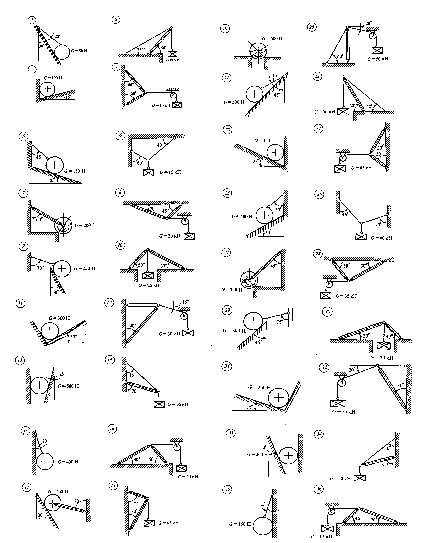
Определить величину и направление реакций связей по данным схемы, показанной на рисунке 1, под действием груза G. Проверить правильность определения реакций.
Расчетно-графическая работа №2 по теме: «Определение реакций опор двухопорной балки»
Последовательность решения задачи:
Изобразить балку вместе с нагрузками.
Выбрать расположение координатных осей, совместив ось Ох с балкой, а ось Оу направив перпендикулярно оси Ох.
Произвести необходимые преобразования заданных активных сил: силу, наклоненную к оси б балки под углом ά, заменить двумя взаимно перпендикулярными составляющими, а равномерно распределенную нагрузку – её равнодействующей, приложенной в середине участка распределения нагрузки.
Освободить балку от опор, заменив их действие реакциями опор, направленными вдоль выбранных осей координат.
Составить уравнения равновесия статики для произвольной плоской системы сил таким образом и в такой последовательности, чтобы решением каждого из этих уравнений было определение одной из неизвестных реакций опор.
Проверить правильность найденных опорных реакций по уравнению, которое не было использовано для решения задачи.