Лекция 20. Определение гамма-процентного ресурса

Вопрос 1. Функция распределения вероятности отказа элементов газотурбинного двигателя

Как было отмечено выше, первоначальную оценку надежно­сти ГТД производят по коэффициентам запаса прочности основ­ных элементов конструкции. Для определения коэффициента за­паса используют расчетные значения действующих и предельных напряжений, рассматривая их как детерминированные величины. Фактически же как действующие, так и предельные напряжения являются случайными величинами, что вызвано случайным ха­рактером силовых и тепловых воздействий на детали двигателя в процессе эксплуатации и нестабильностью прочностных свойств материалов. Поэтому условие прочности деталей необхо­димо рассматривать в вероятностном смысле, определяя вероят­ность их неразрушения в пределах заданного ресурса.

Пусть случайные величины действующих и предельных напряжений имеют некоторые плотности вероятностей и (рис. 125).

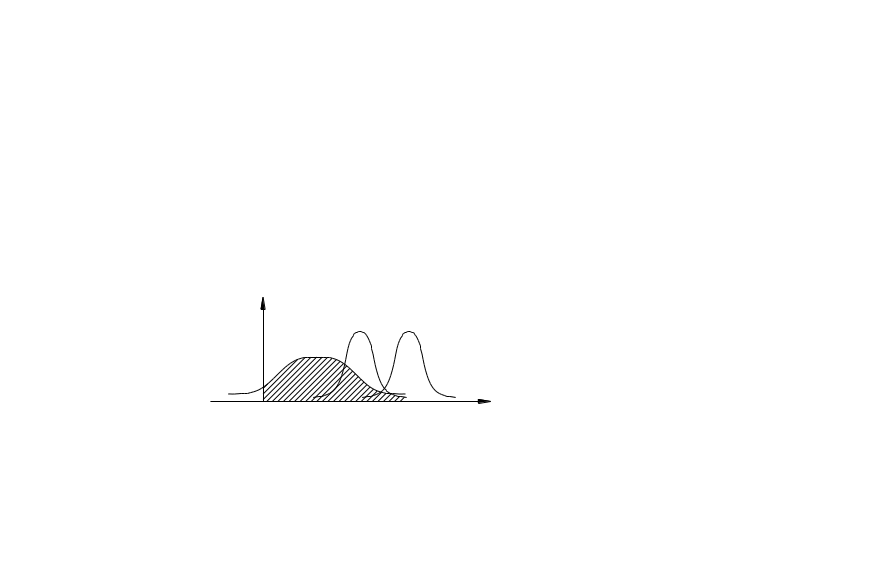
Рис.125. Плотности распределений напряжений и и их разности

Плотность вероятности для разности этих напряжений можно найти, используя формулу ком­позиции двух законов распределения:

Прочность детали будет обеспечена (с некоторой вероят­ностью неразрушения Р) в том случае, если предельные напря­жения будут не меньше действующих, т. е. при . Согласно этому условию, вероятность неразрушения детали на­ходим по формуле:

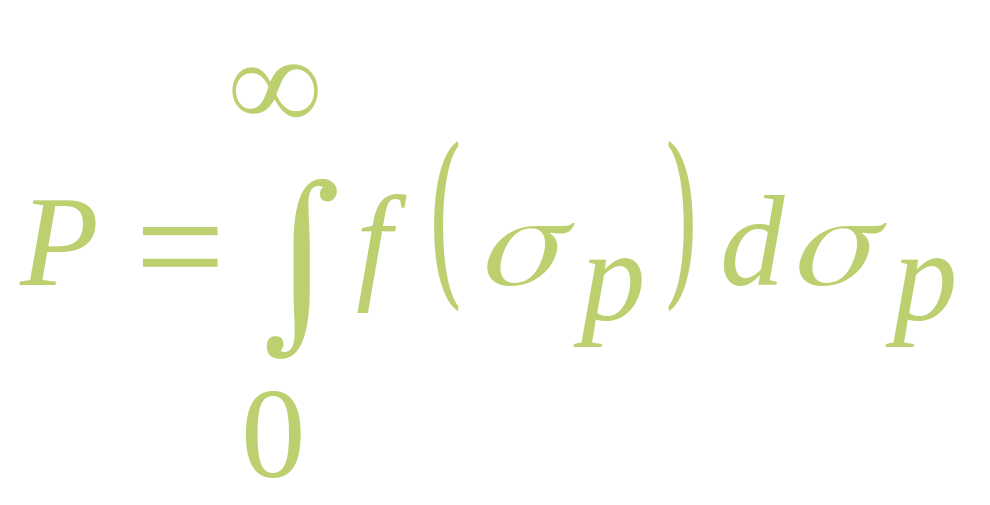
В геометрическом смысле вероятность Р равна площади под кривой распределения в области положительных значений .

Предположим, что напряжения и распределены по нормальному закону с плотностями вероятностей

,

.

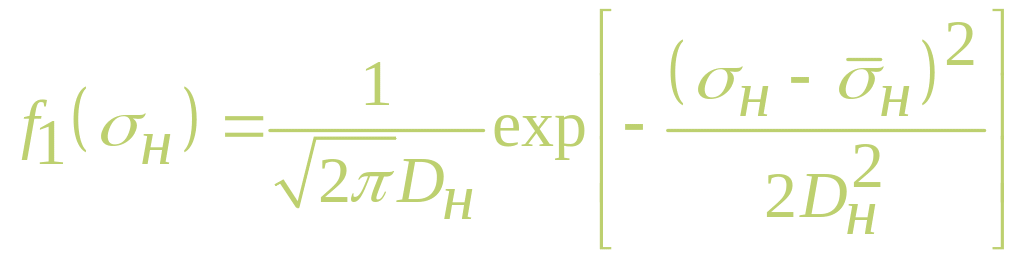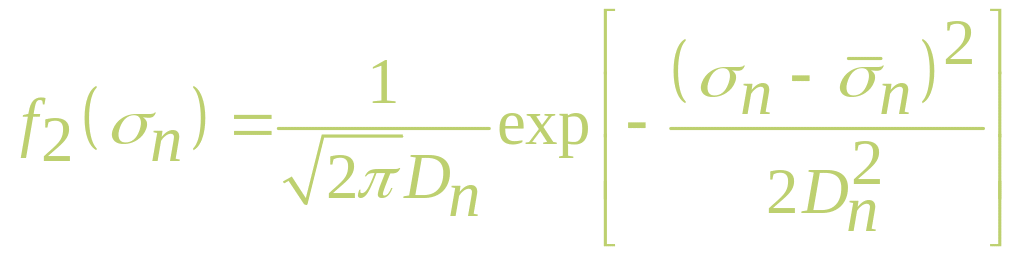где — математические ожидания соответствующих напря­жений, — их дисперсии.

Подставляя функции распределения в соотношения композизии двух законов распределения и вероятность неразрушения и выполняя интегрирование, получим:

,

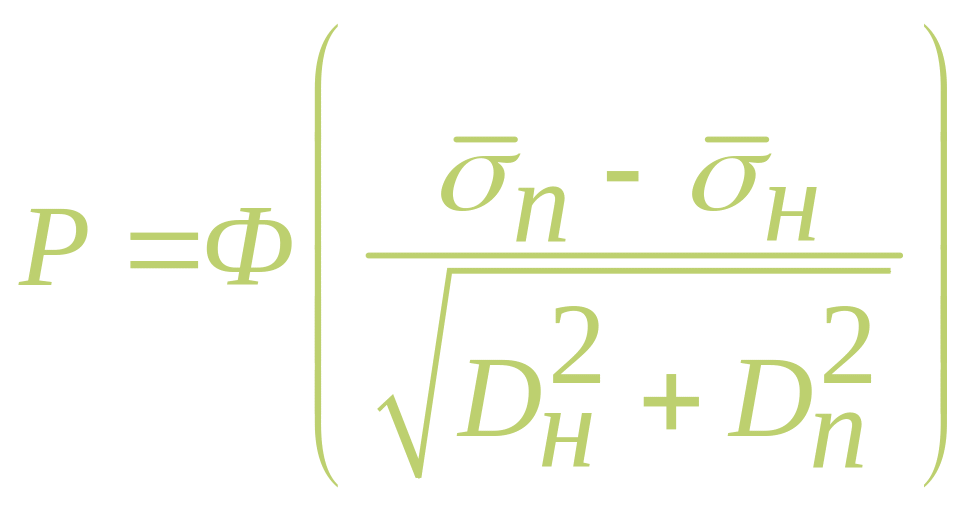где 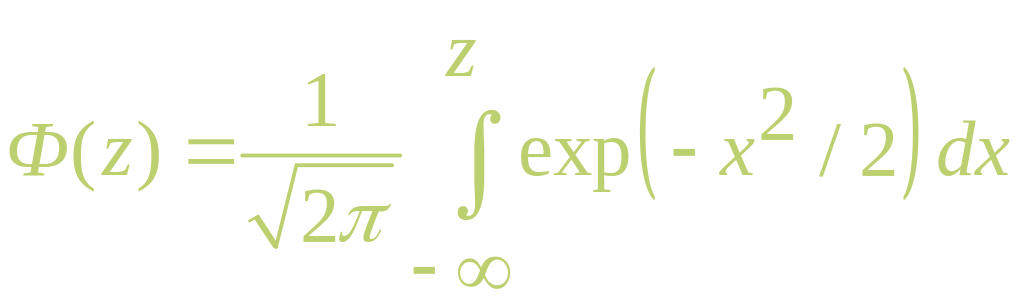— функция нормального распределения, значения которой можно найти по таблицам или методами численного интегрирования.

Введем в рассмотрение коэффициент запаса прочности и коэффициенты вариации напряжении и . Относительно этих параметров формула вышеприведенная формула вероятности бу­дет иметь следующий вид:

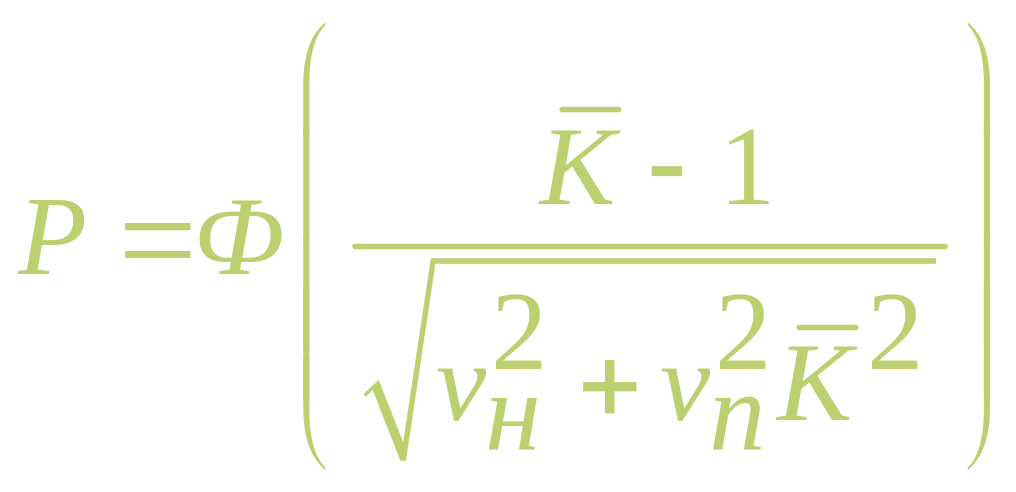
Анализируя данную формулу и построенные с ее помощью графики (рис.126), отметим, что вероятность неразрушения конструктивного элемента существенно зависит от коэффициента запаса прочности и параметров случайной колеблемости дей­ствующих и предельных напряжений. Эти зависимости необходи­мо учитывать при нормировании величин коэффициентов запаса прочности, оценивающих надежность элементов ГТД в пределах назначаемого ресурса.

Рис.126. Зависимости вероятности неразрушения конструктивного элемента от расчетного коэффициента запаса прочности:

1 – ; 2 – ; 3 – ; 4 – ; 5 –

Вопрос 2. Плотность распределения вероятности отказа элементов газотурбинного двигателя

В качестве критерия надежности ГТД целесообразно исполь­зовать гамма-процентный ресурс, обеспечивающий возможность нормирования предельных величин наработки конструктивных элементов по уровням вероятностей их неразрушения.

Гамма-процентный ресурс с высокой вероятностью неразрушения соответствует на -характеристике ГТД началу периода старения, которое статистическими методами определить нельзя, так как массовые постепенные отказы основ­ных элементов двигателя недопустимы в эксплуатации по услови­ям безопасности полетов. Поэтому гамма-процентный ресурс не­обходимо уметь прогнозировать с помощью физических моделей отказов, основанных на анализе конкретных причин поврежде­ний деталей ГТД.

При расчете ресурса деталей горячей части ГТД (например, рабочих лопаток турбин) с помощью кривых длительной прочности материалов обычно оценивают повреждения, вызванные дей­ствием статических напряжений , (рис. 127) при соответствую­щих температурах , на основных эксплуатационных режимах (взлетном — 1, номинальном — 2, крейсерском — 3).

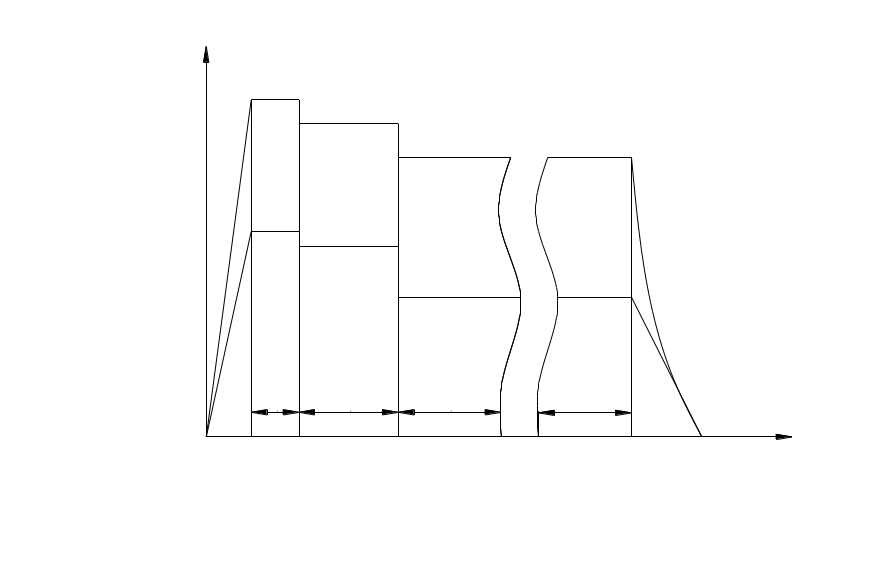
Рис.127. Упрощенная схема изменения температуры и напряжений , действующих на элемент ГТД в течение полета продолжительностью

Степень длительных статических повреждений деталей, накопленных за весь эксплуатационный цикл работы ГТД от запуска до остано­ва определяют в соответствии с принципом линейного суммиро­вания повреждений по следующей формуле:

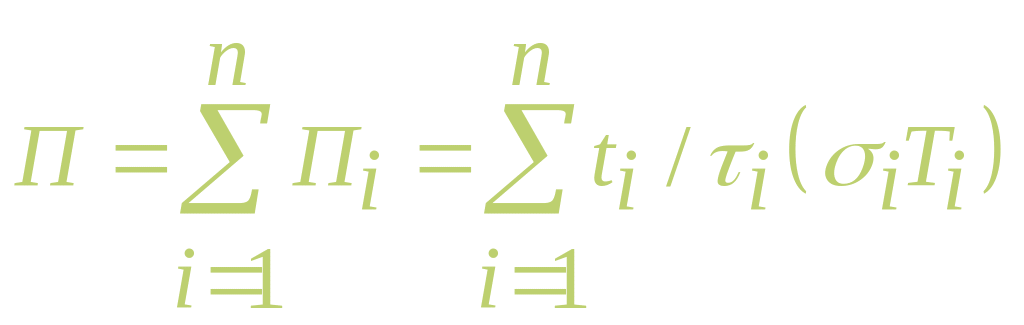
где — число стационарных режимов работы двигателя в эксплуатационном цикле; – повреждение конструктивного элемента на этих режимах; —длительность режимов; — функция длительной прочности материала, позволяющая найти значения времени до разрушения элемента под действием напряжения при температурах .

Даже при фиксированных значениях и из-за нестабильности свойств материалов время до разрушения является случайной величиной, для которой характерно логарифмически нормальное распределение .

Если известна некоторая априорная совместная плотность распределения напряжений и температур , то плотность распределения времени до разрушения на основании формулы полной вероятности

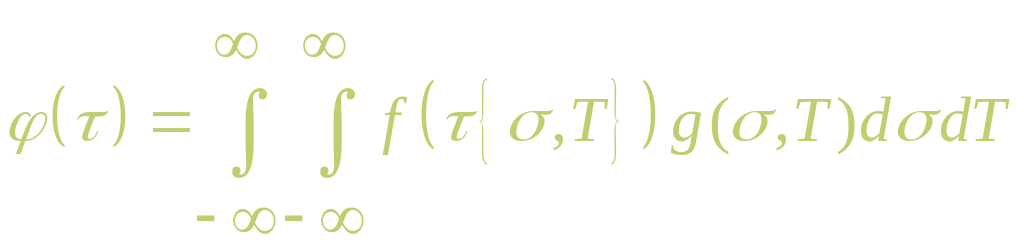
Определив для каждого -го режима нагружения функции распределения и используя найденные в результате статистической обработки наблюдений плотности вероятностей для продолжительностей режимов , находим плотности вероятностей для каждого этапа и плотность распределения суммы независимых величин .

Данная функция описывает распределение случайной по­врежденности элемента ГТД за один полетный цикл (плотность распределения вероятности отказа). За неко­торое число N полетных циклов накопленное повреждение можно найти с помощью гипотезы линейного суммирования повреждений по формуле

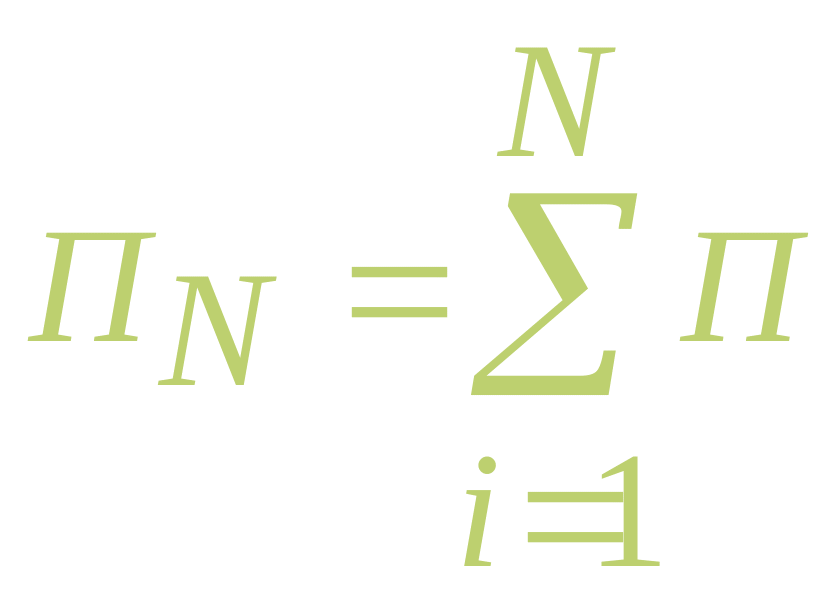
Литература

1. Лозицкий Л.П. Конструкция и прочность авиационных газотурбинных двигателей. – М.: Воздушный транспорт, 1992.

2. Когге Ю.К., Майский Р.А. Основы надежности авиационной техники. – М.: Машиностроение, 1993.