Лекция 16. Прогнозирование надежности ат

Вопрос 1. Оценка эксплуатационной надежности ат при различных стратегиях технической эксплуатации (задачи и назначение)

Вопрос 2. Методы составления прогнозов

К решению задачи прогнозирования существуют два подхода — детерминированный и стохастический.

Модель системы называют детерминированной, если входящие в нее описания воздействия и параметры модели являются постоянными или детерминированными функциями пере­менных состояния и времени. Модель системы называют стохастической, если функции, описы­вающие воздействия и параметры модели, являются случайными функциями или случайными величинами. Для стохастических (ве­роятностных) динамических систем текущее состояние в момент и входное воздействие определяют в мо­мент не , а лишь его вероятностное распределение.

В первом случае задача сводится к отысканию аппроксимирующего выражения, во втором в качестве прогнозируемой характеристики принимается реализация случайной величины, определяющая интервал времени от момента контроля до первого пересечения поля допуска прогнозируемой величины. Поскольку процессы износа, старения машин, обусловливающие развитие постепенных отказов, являются случайными величинами, более общий характер носит стохастический подход.

В настоящее время разрабатывается третий метод прогнозирования — метод распознавания образов. Метод предполагает разбиение всей группы изделий на несколько классов (групп) в соответствии с признаками каждого класса. Между классами устанавливаются строгие границы. Процесс создания образа разбит на три этапа: «обучение», создание образа, «экзамен». Процесс индивидуального прогнозирования надежности методом распознавания образов сводится к отнесению данной электрической машины к тому или иному классу на основании критериев работоспособности, причем для каждого класса должны быть априорно известны показатели надежности и технические характеристики.

Лекция 17. Прогнозирование технического состояния объекта ат

Вопрос 1. Прогнозирование параметров

Задача прогнозирования Т.С. одномерного объекта формулируется следующим образом: пусть контролируемый параметр «Х» (например, диаметр вала в подшипнике скольжения) объекта в моменты контроля принимает значения , по которым построен график (рис.123). Необходимо по известным значениям , где в моменты времени в прошлом, предсказать значения для моментов времени в будущем.

Рис.123. график изменения параметра Х по времени

Если период между очередными моментами контроля равен (например, 100часов), то прогнозируемый период равен .

Для прогнозирования параметров может использоваться линейная интерполяция – замена функции алгебраическим двучленом , однако ввиду появления больших погрешностей ее практически не используют.

При монотонной функции ее математическое представление, выраженное в виде интерполяционной формулы Лагранжа, будет иметь вид полинома порядка .

,

где - коэффициент Лагранжа, вычисляемый математически.

.

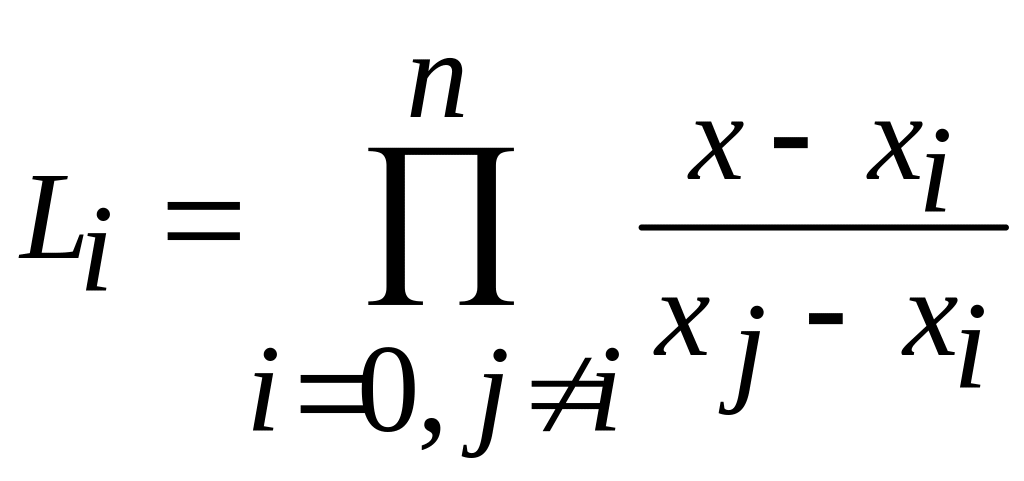Ошибка прогнозирования при этом не превышает 10-15%, если количество предыдущих точек контроля .

Для прогнозирования может быть использована интерполяционная формула Ньютона. Интерполяционные полиномы в форме Ньютона удобно использовать, если точка интерполировании находится вблизи начала (прямая формула Ньютона) или конца таблицы (обратная формула Ньютона).

Если узлы интерполяции равноотстоящие и упорядочены по величине, так что x_{i + 1} − x_i = h = const, то есть x_i = x₀ + ih, то интерполяционный многочлен можно записать в форме Ньютона.

где , а выражения вида Δ^ky_i — конечные разности.