Лабораторная работа № 1 Анализ систем с применением марковских процессов.

Аппарат марковских случайных процессов широко используется при анализе сложных систем управления для описания их поведения при наличии случайных факторов.

Пусть имеется случайный процесс, протекающий в системе с возможными состояниями Z₀,Z₁,…Z_i,…Z_j.. Обозначим условную вероятность того, что в момент t =t₀+T система будет в состоянии Zj,если в момент t₀ она была в состоянии Z_i через P_ij(t₀,Т). Дискретный случайный процесс называется марковским, если вероятность Р_ij(t₀,Т) зависит только от i,j,t₀,T,т.е только от того, в каком состоянии система была в момент t₀ и в какое состояние она перейдет через время Т.

М арковским процессом с непрерывным временем называется процесс, у которого переход из одного состояния в другое возможен в любой момент времени. Такой класс процессов широко используется для анализа поведения сложных систем управления.

Для описания поведения системы в классе марковских процессов с непрерывным временем необходимо:

1. Ввести понятие состояния системы.

2. Указать все состояния, в которых может находиться система.

3. Составить граф состояний, т.е. указать пути возможных непосредственных переходов системы из состояния в состояние.

4. Для расчета переходных процессов в системе указать, в каком состоянии находится система в начальный момент времени.

5. Для каждого возможного перехода на графе указать интенсивность ij потока событий, переводящих систему из состояния Zi в состояние Zj. Обычно интенсивности ij определяются экспериментально.

Исчерпывающей характеристикой марковского процесса является совокупность вероятностей Pj(t) того, что процесс в момент времени t будет находиться в состоянии Zj . Эти вероятности определяются на основе решения системы дифференциальных уравнений:

Система (1) определяет переходной процесс в предположении, что начальное состояние –P₀.

Если число состояний системы n-конечно и из каждого состояния графа можно перейти в любое другое состояние, то такая система будет иметь предельный стационарный режим. Так, система рис.1а имеет стационарный режим, а система рис.1б - не имеет.

(а) Рис.1 (б)

С практической точки зрения представляет интерес определение вероятностей состояний системы в предельном стационарном режиме.

Для их расчета используется система алгебраических уравнений, получающаяся из (1) путем приравнивания к нулю производных:

С истема (3) является линейно зависимой, поэтому ее следует дополнить условием:

Пример. Два абонента А и В работают с одним информационным центром. В определенный момент времени центр может обслуживать только одного абонента. Абонент А имеет более высокий приоритет, поэтому, если от А приходит заявка, обслуживание В прекращается до окончания обслуживания А.

1. Рассчитать вероятности возможных состояний данной системы, если известны интенсивности потоков событий, переводящих систему в соседние состояния.

2. Выяснить, будет ли система работать эффективно, если для этого необходимо, чтобы потери времени абонента В на ожидание составили бы не более 50% времени его обслуживания.

3. Установить какие параметры и каким образом должны измениться, чтобы повысилась эффективность обслуживания абонента В?

Введем понятие состояния системы. Состояние системы определяется состоянием абонентов А и В. Для абонента А возможны два состояния: 0 – отсутствие заявки; 1 – обслуживание. Для абонента В возможны три состояния: 0 – отсутствие заявки; 1 – обслуживание; 2 – ожидание обслуживания.

Тогда состояния системы следующие:

(0,0) – 1 – отсутствие заявок от А и В;

(0,1) – 2 – отсутствие заявки от А и обслуживание В;

(1,0) – 3 – обслуживание А и отсутствие заявки от В;

(1,2) – 4 – обслуживание А и ожидание обслуживания для В.

Г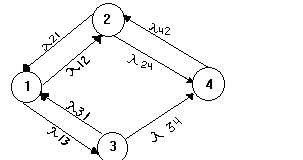 раф состояния системы имеет вид:

Рис.2

В соответствии с (3) составим систему алгебраических уравнений для определения вероятностей состояний P_i , i=1,4:

–(12+13)Р1+21Р2+31Р3=0

–(21+24)Р2+ 42Р4+12Р1=0 (5)

–(31+34)Р3+13Р1=0

–42Р4+24Р2+34 Р3=0

Систему уравнений можно составить непосредственно по графу рис.2, пользуясь правилом: для каждого i-го состояния составляется одно уравнение, причем исходящие из i интенсивности  берутся со знаком минус и умножаются на Pi ; входящие в i интенсивности умножаются со знаком плюс на вероятности тех состояний, из которых они исходят.

Допустим интенсивности для графа рис.2 заданы и равны: ; ; ; ; . Тогда система (5) примет вид :

Это система линейно-зависимых уравнений. Поэтому одно уравнение (неважно какое) системы необходимо заменить условием (4):

(6)

Решая систему (6), например, методом Гаусса, получим:

; ; ; .

Отношение времени ожидания и времени обслуживания абонента В определяется отношением вероятностей состояний Р4 и Р2:

Т.к. это отношение больше 0,5 (50%), то можно сделать вывод о неэффективности работы системы.

Чтобы уменьшить отношение необходимо уменьшить интенсивность потоков ₂₁,₃₄ и ₂₄ или увеличить интенсивность потоков ₁₂ и₄₂.

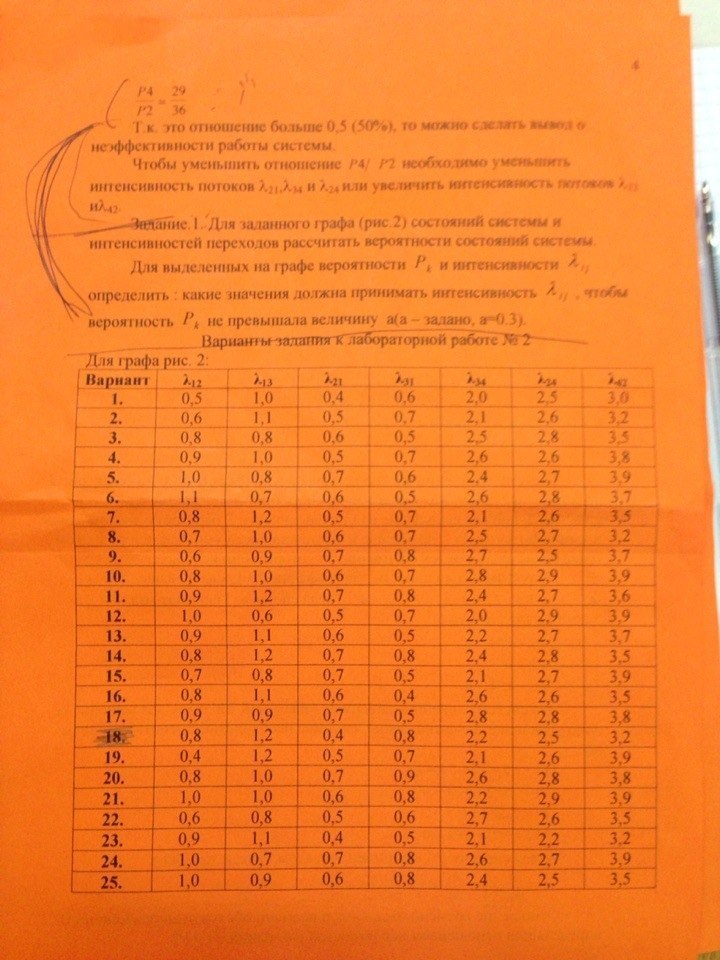
Задание.1. Для заданного графа состояний системы и интенсивностей переходов рассчитать вероятности состояний системы.

Для выделенных на графе вероятности и интенсивности определить : какие значения должна принимать интенсивность , чтобы вероятность не превышала величину а(а - задано).