5 Тема: Аналитическая геометрия в пространстве

Общее уравнение плоскости.

В пространстве существует единственная плоскость, проходящая через заданную точку М перпендикулярная к нормальному вектору n. Уравнение этой плоскости относительно данной системы координат имеет вид:

Ax+By+Cz+D=0 (1)

Уравнение (1) называется общим уравнением плоскости.

(2)

а уравнение (2)— уравнением плоскости, проходящей через точку М (х₁ ,y₁ ,z₁) перпендикулярно к вектору п = (А, В, С).

Расстояние от точки до плоскости. Пусть даны точка М₀ (x₀, y₀, z₀) и плоскость

Аx+By+Сz+D=О. (3)

Тогда расстояние от точки до плоскости находится по формуле

(4)

Угол между двумя плоскостями находится как угол между векторами нормалями плоскостей по известной формуле

Условие параллельности и перпендикулярности двух плоскостей.

Условия паралельности имеют вид:

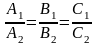(5)

Если плоскости взаимно перпендикулярны, то векторы n₁ и n₂ будут также взаимно перпендикулярны, и их скалярное произведение должно быть равно нулю:

А₁A₂ + В₁B₂ + С₁C₂ = О (7)

Прямая в пространстве.

Каноническое уравнение прямой, заданной точкой М₀(x₀,y₀,z₀) и направляющим вектором имеет виді:

(8)

а векторное уравнение: 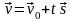(9)

параметрическое уравнение :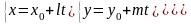 (10)

Каноническое уравнение прямой проходящей через две точки

(11)

а параметрическое урвнение: (12)

Уравнение прямой заданной как пересечение двух плоскостей

(13)

Для того чтобы две прямые L₁ и L₂ в пространстве были ортогональнынеобходимо и достаточно, чтобы

, (14)

а для того чтобы они были паралельны необходимо выполнение условия 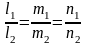(15)

6 Тема: кривые второго порядка

Окружность и ее уравнение

В прямоугольной системе координат окружность радиусом R с центром в точке С

(а, Ь) задается уравнением

( x - a)² +( y - b)² = R² (1)

где х, у — координаты произвольной точки М окружности.

Эллипс и его каноническое уравнение

Определение Эллипсом называется множество точек плоскости, сумма расстояний от которых до двух данных точек (фокусов эллипса) есть величина постоянная (большая, чем расстояние между фокусами).

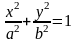
Постоянную величину, входящую в определение эллипса, обозначим через 2а (а>О), а расстояние между фокусами —2с

Свойство 1. Координатные оси являются осями симметрии эллипса, а начало координат — его центром симметрии.

Свойство 2. Эллипс пересекает координатные оси в точках Аi(-а, 0),А2(а, 0), Ъ) и В2(0, —Ь).

Свойство 3. Координаты к и у любой точки эллипса удовлетворяют условиям: —а ≤х ≤а, −b ≤ y ≤ b.

Свойство 4. для точек эллипса, расположенных в первой координатной четверти, с возрастанием их абсциссы х от О до а ордината у убывает от b до О.

Оси координат называются осями симметрии, а начало координат — центром эллипса.

Эксцентриситет эллипса

Определение. Отношение фокусного расстояния к длине большой оси эллипса называется эксцентриситетом эллипса. Эксцентриситет

обозначим буквой е. По определению ,

ε = =

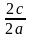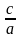
Гипербола и ее каноническое уравнение

Определение 11.3. Гиперболой называется множество точек плоскости, абсолютная величина разности расстояний от каждой из которых до двух данных точек, называемых фокусами гиперболы, есть величина постоянная (меньшая, чем расстояние между фокусами).

Свойство 1. Координатные оси являются осями симметрии, а начало координат — центром симметрии гиперболы.

Свойство 2. Гипербола пересекает ось абсцисс в точках Аi (—а, 0) и А_j,{а, 0) и не пересекает ось ординат.

Свойство 3. Координаты х и у любой точки гиперболы могут изменяться в пределах \х\ ≥ а, - ∞ < y <+ ∞.

Определение. Прямые, проходящие через начало координат и имеющие угловые коэффициенты Ь/а и — Ь/а, называются асимптотами гиперболы, заданной уравнением .

Определение Гипербола, полуоси которой равны между собой, называется равносторонней.

Определение Отношение фокусного расстояния гиперболы к ее действительной оси называется эксцентриситетом гиперболы

Как и в случае эллипса, эксцентриситет гиперболы обозначим буквой е. По определению для гиперболы

ε= =

Парабола и ее каноническое уравнение

Определение. Параболой называется множество точек плоскости, каждая из которых находится на одинаковом расстоянии от данной точки, называемой фокусом параболы, и данной прямой, называемой директрисой.

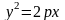
Свойство 1. Абсцисса любой точки параболы больше нуля.

Свойство 2. Парабола проходит через начало координат.

Свойство 3. Парабола симметрична относительно оси абсцисс.

Свойство 4. При неограниченном возрастании абсциссы х ордината у возрастает

Теорема Отношение расстояния от любой точки эллипса (гиперболы) до фокуса к расстоянию до соответствующей директрисы, есть величина постоянная, равная эксцентриситету эллипса (гиперболы).