1.6.2 Питання для самоконтролю
Загальна характеристика й основні види послідовних коригуючих пристроїв.
Введення похідної від похибки в структуру САК.
Введення інтеграла від похибки в структуру САК.
Ізодромний коригуючий пристрій.
Загальна характеристика і основні види паралельних коригуючих пристроїв.
Коригуючі пристрої за зовнішнім впливом.
Неодиничні зворотні зв’язки.
Загальна характеристика коригуючих пристроїв і еквівалентність їх різних типів.
Загальна характеристика і основні види паралельних коригуючих пристроїв у виді місцевих зворотних зв’язків.
2 Завдання до контрольних робіт
2.1 Завдання для контрольної роботи за темами «Математичний опис елементів та систем керування» та «Стiйкiсть лiнійних систем автоматичного керування»:
1. Скласти диференціальне рівняння в операторній формі для ланки у вигляді електричного кола та знайти вираз для передавальної функції.
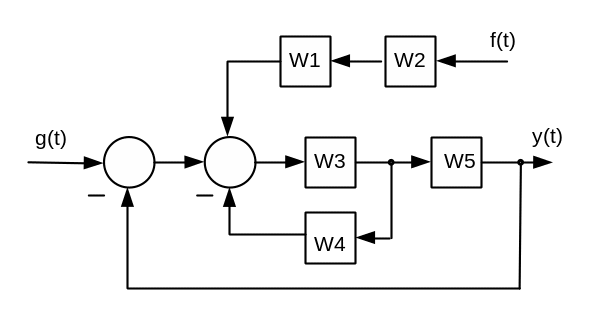
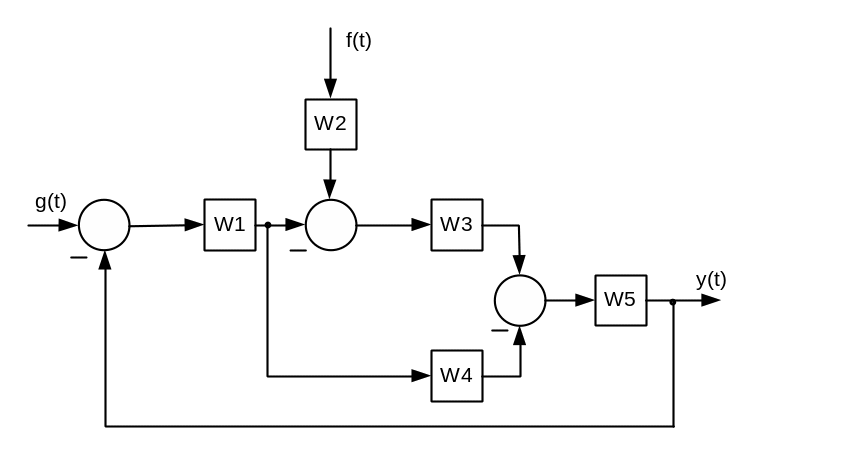
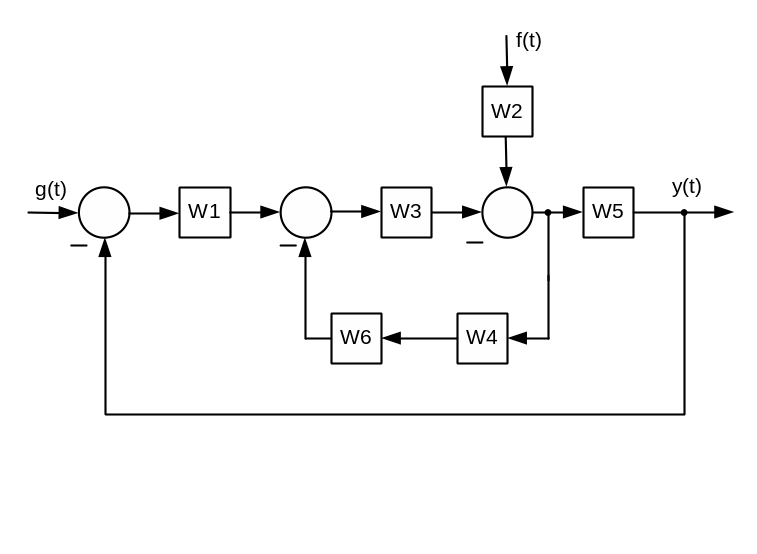
2. Знайти вираз для передавальної функції розімкненого кола.
3. Знайти вираз для передавальних функцій замкненої системи.
4. Користуючись критерієм Гурвиця, оцiнити стiйкiсть системи з заданим характеристичним рiвнянням.
5. Задано передавальну функцiю розімкненої системи. Визначити вираз для заданого параметру, при якому замкнена система буде знаходитись на коливальній межi стiйкостi.
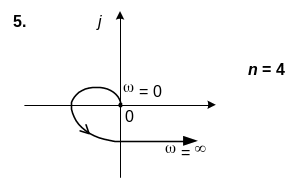
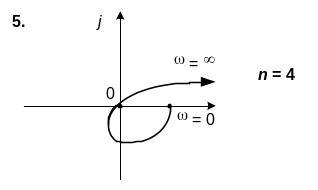
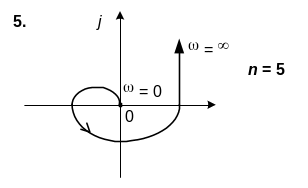
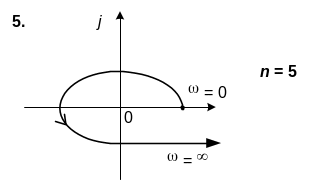
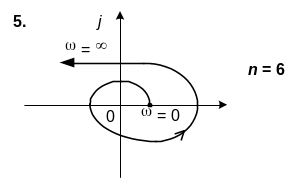
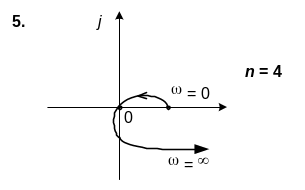
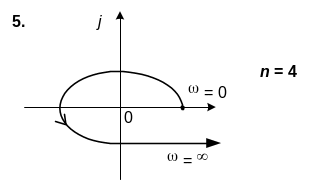
6. САК описується характеристичним рiвнянням n-го порядку. Використовуючи вид кривої Михайлова, зробити висновок щодо стiйкостi системи.
Варіант № 1
1.
UВХ(t)
UВиХ(t)
2.
3.
4.
5.
6. n=4
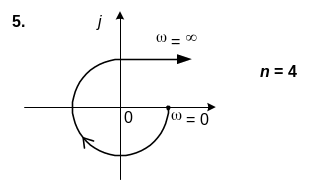
Варіант № 2
1.
UВХ(t)
UВиХ(t)
2.
3.
4.
5.
6. n=5
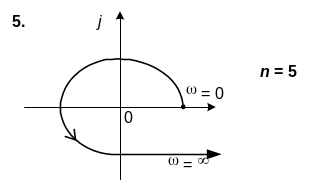
Варіант № 3
1.
UВХ(t)
UВиХ(t)
2.
3.
4.
5.
6. n=5
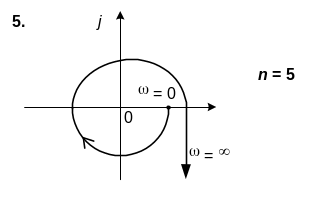
Варіант № 4
1.
UВХ(t)
UВиХ(t)
2.
3.
4.
5.
6. n=4
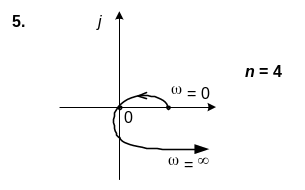
Варіант № 5
1.
UВХ(t)
UВиХ(t)
2.
3.
4.
5.
6. n=6
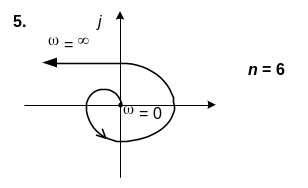
Варіант № 6
1.
UВХ(t)
UВиХ(t)
2.
3.
4.
5.
6. n=5
Варіант № 7
1.
UВХ(t)
UВиХ(t)
2.
3.
4.
5.
6. n=5
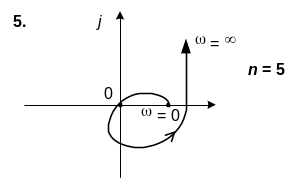
Варіант № 8
1.
UВХ(t)
UВиХ(t)
2.
3.
4.
5.
6. n=4
Варіант № 9
1.
UВХ(t)
UВиХ(t)
2.
3.
4.
5.
6. n=4
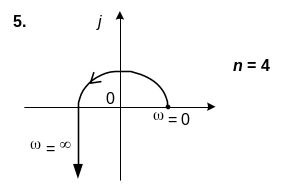
Варіант № 10
1.
UВХ(t)
UВиХ(t)
2.
3.
4.
5.
6. n=6
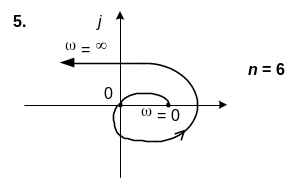
Варіант № 11
1.
UВХ(t)
UВиХ(t)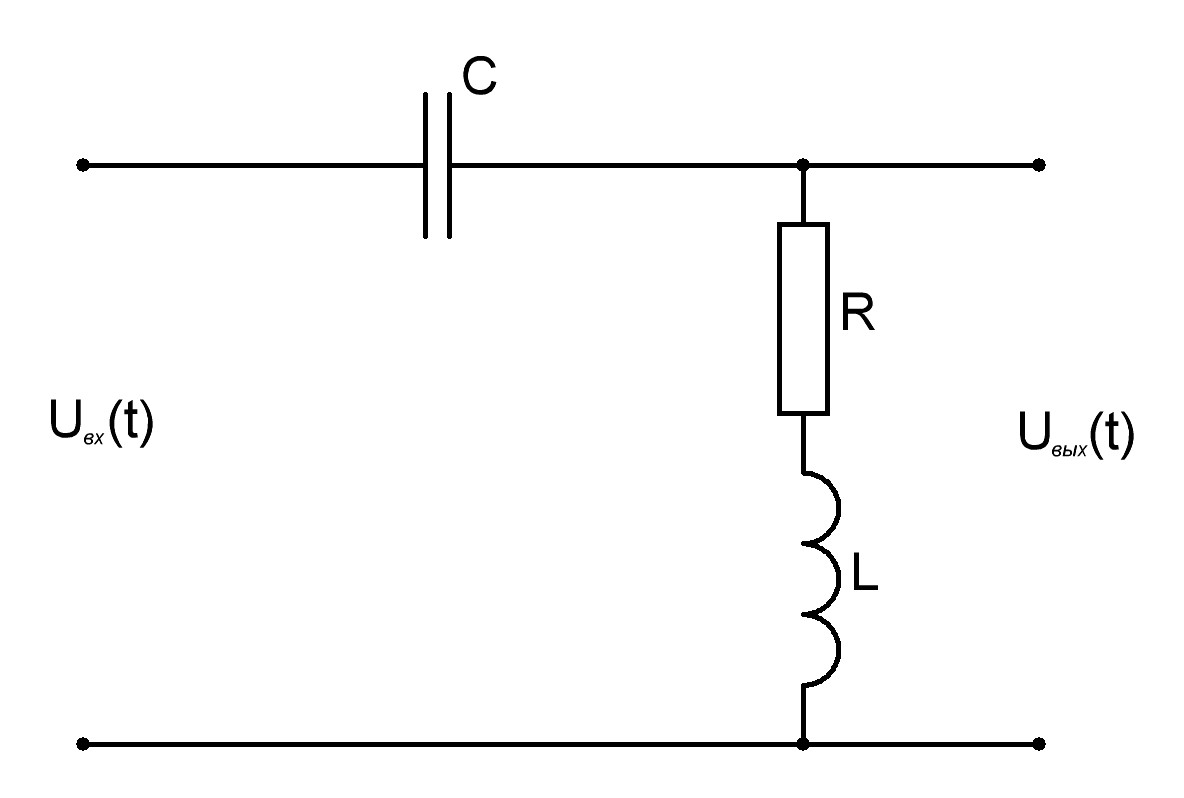
2.
3.
4.
5.
6. n=3
Варіант № 12
1.
UВХ(t)
UВиХ(t)
2.
3.
4.
5.
6. n=4
Варіант № 13
1.
UВХ(t)
UВиХ(t)
2.
3.
4.
5.
6. n=4
Варіант № 14
1.
UВХ(t)
UВиХ(t)
2.
3.
4.
5.
6. n=5
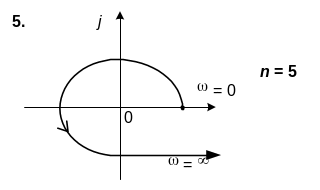
Варіант № 15
1.
UВХ(t)
UВиХ(t)
2.
3.
4.
5.
6. n=6
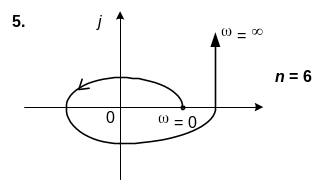
Варіант № 16
1.
UВХ(t)
UВиХ(t)
2.
3.
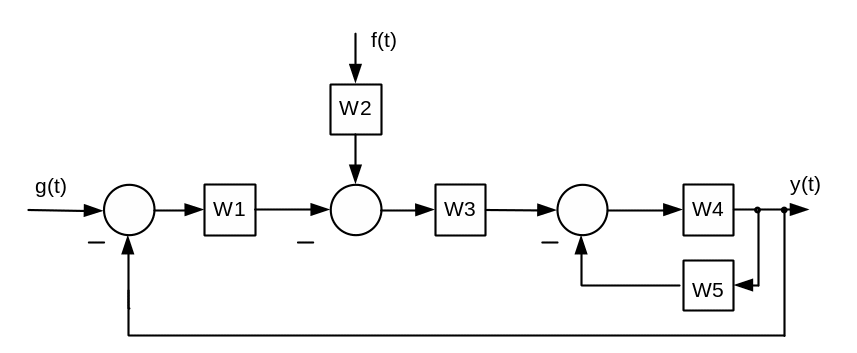
4.
5.
6. n=4
Варіант № 17
1.
UВХ(t)
UВиХ(t)
2.
3.
4.
5.
6. n=4
Варіант № 18
1.
UВХ(t)
UВиХ(t)
2.
3.
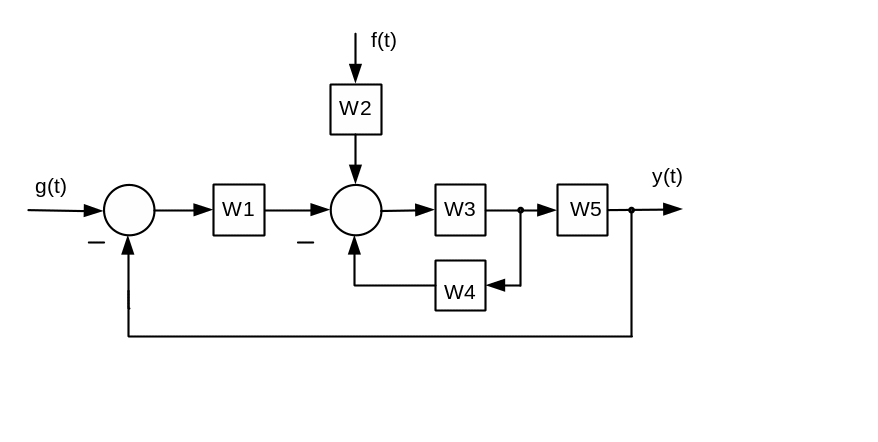
4.
5.
6. n=5
Варіант № 19
1.
UВХ(t)
UВиХ(t)
2.
3.
4.
5.
6. n=5
Варіант № 20
1.
UВХ(t)
UВиХ(t)
2.
3.
4.
5.
6. n=6
Варіант № 21
1.
UВХ(t)
UВиХ(t)
2.
3.
4.
5.
6. n=4
Варіант № 22
1.
UВХ(t)
UВиХ(t)
2.
3.
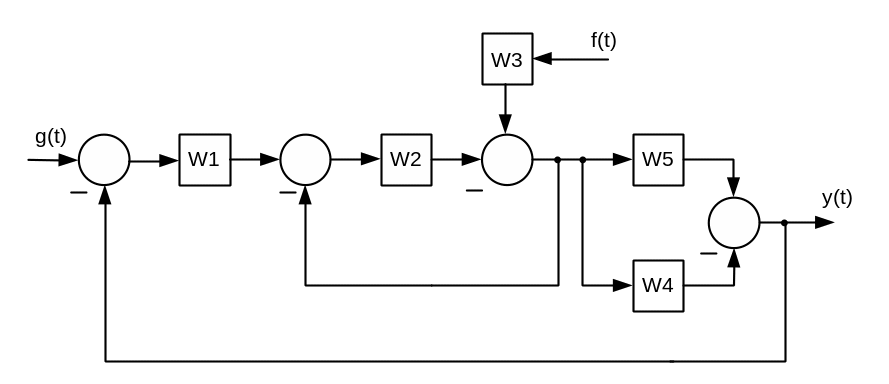
4.
5.
6. n=4
Варіант № 23
1.
UВХ(t)
UВиХ(t)
2.
3.
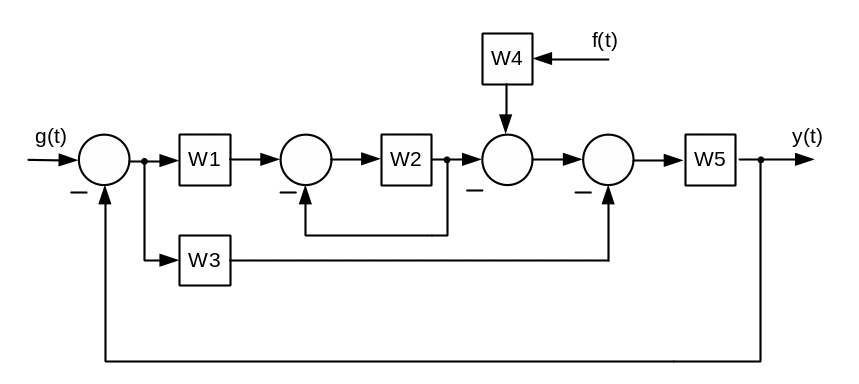
4.
5.
6. n=4
Варіант № 24
1.
UВХ(t)
UВиХ(t)
2.
3.
4.
5.
6. n=4
Варіант № 25
1.
UВХ(t)
UВиХ(t)
2.
3.
4.
5.
6. n=5
