Индексированные переменные и итерация

• Ввод и задание индексированной переменной.

• Задание значений индексированных переменных по итерационным формулам.

Обозначение индексированной переменной есть имя переменной с указанием индекса (индексов):

Ввод Как выглядит

x[j x_j

y[(i-1) y_i-1

a[(i,j) a_i,j

Задание индексированной переменной осуществляется с помощью оператора присваивания:

имя_индексированной_переменной := выражение

При этом диапазон изменения индекса (индексов) должен быть заранее задан. Например,

1. j:=1..5 yj:=xj sin[xj]

2. i:=1..3 j:=1..3 ai,j:=i+j

Также значения индексированных переменных можно вычислять по итерационным формулам. Например,

i:=1..5 z₀:=1 z_j:=z_j-1+1.2

Таблицы ввода и вывода

• Ввод значения индексированной переменной в виде таблицы.

• Вставка элементов в таблицу.

• Удаление элемента таблицы.

• Вывод значения индексированной переменной в виде таблицы.

Чтобы ввести значения индексированной переменной в виде таблицы:

1) Задайте диапазон изменения индексной переменной (например, i:=1..10).

2) Введите индексированную переменную, например xi.

3) Введите оператор присваивания := .

4) Введите элементы таблицы (числа, выражения), разделяя их запятой.

Замечание: Первый элемент таблицы вводится непосредственно после знака присваивания. После ввода символа-разделителя формируется таблица.

В ведите x[i:100, чтобы увидеть

Чтобы осуществить вставку в таблице, установите курсор на конец элемента таблицы (после которого необходима вставка значения(ий)), введите символ "запятая" и затем число (или выражение) в отведенное "знакоместо". Если добавляемых чисел несколько, ввод каждого (кроме последнего) оканчивайте вводом символа "запятая". Чтобы удалить элемент таблицы, установите курсор на его конец и нажмите клавишу [BackSpace].

Замечание: При задании индексированной переменной с двумя индексами помните, что первым меняется второй индекс.

Чтобы получить значения выражений, содержащих переменную-индекс, или значения индексированных переменных в виде таблицы, достаточно ввести выражение (индексированную переменную) и следом за ним знак равенства.

Например, пусть i:=1..4 xi:=20 i

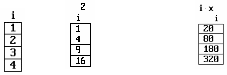Ввод i= i^2 = x[i= i*x[i=

К ак выглядит

Пример табуляции функции

Таблица значений функции f(x) для значений x, изменяющихся от x0 до xk c шагом h.

Аналогично заданию переменной-индекса можно задать диапазон изменения любой другой переменной и использовать ее при организации циклических процессов.

П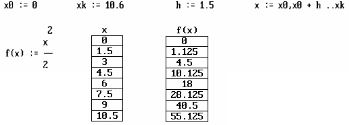 ример. Получить таблицу значений функции f(x) для значений x, изменяющихся от x0 до xk, с шагом h. MathCAD-документ:

Решение уравнений средствами Mathcad

Как известно, многие уравнения и системы уравнений не имеют аналитических решений. В первую очередь это относится к большинству трансцендентных уравнений. Доказано также, что нельзя построить формулу, по которой можно было бы решить произвольное алгебраическое уравнение степени выше четвертой. Однако такие уравнения могут решаться численными методами с заданной точностью (не более значения заданного системной переменной TOL).

Численное решение нелинейного уравнения

Для простейших уравнений вида f(x) = 0 решение в Mathcad находится с помощью функции root (Рисунок 5).

root( f(х1, x2, …), х1, a, b )

Возвращает значение х1, принадлежащее отрезку [a, b], при котором выражение или функция f(х) обращается в 0. Оба аргумента этой функции должны быть скалярами. Функция возвращает скаляр.