Элементарные математические встроенные функции

1) Тригонометрические (аргумент в радианах):

sin(x), cos(x), tan(x)

2) Обратные тригонометрические (результат в радианах):

asin(x), acos(x), atan(x)

3) Гиперболические:

sinh(x), cosh(x), tanh(x)

4) Обратные гиперболические:

asinh(x), acosh(x), atanh(x)

5) Другие:

exp(x) экспонента

ln(x) натуральный логарифм

log(x) десятичный логарифм

Re(z) вещественная часть числа z

Im(z) мнимая часть числа z

arg(z) аргумент комплексного числа z

floor(x) наибольшее целое < x (x - вещест.)

ceil(x) наименьшее целое > x (x - вещест.)

angle(x,y) угол (в радианах), образуемый вектором (x,y) с

положительным направлением оси x

mod(x,y) остаток от деления x на y (x,y - вещественные)

rnd(x) случайное число из промежутка [0,x]

и т.д.

Замечания:

1) Имена функций следует вводить в том виде, в каком они перечислены выше. Так, в MathCADе имя SIN не является именем функции.

2) Для вычисления нового случайного числа нужно установить курсор на выражение, содержащее функцию rnd(x), и нажать клавишу F9. Начальное число для датчика псевдослучайных чисел устанавливается командой Randomize═[нач.число]. Команда Randomize без параметра выводит текущее начальное число для датчика псевдослучайных чисел (по умолчанию 1) и дает возможность его изменить.

Выражение в MathCADе есть совокупность имен переменных, чисел, функций, соединенных знаками операций и отношений.

Аргументами встроенных функций могут быть константы, переменные, функции, выражения.

Функции, определяемые пользователем

• Вид равенства для определения собственной функции.

• Глобальное округление часто используемых функций.

Чтобы определить свою собственную функцию, введите равенство вида:

FuncName( аргументы ) := выражение

Здесь FuncName - имя функции, аргументы - список элементов, разделенных запятыми.

Аргументами функций могут быть переменные или имена функций.

Например:

Задание функции Обращение

f(x):= cos(x) + 2 f(1.8)

f(cos(3))

dist(1.5,cos(4),a)

(значение a должно быть задано перед обращением)

diff(f1,f2,x):=f1(x)-f2(x) diff(cos,sin,4)

Замечание: Все входящие в выражение параметры, если они не являются аргументами определяемой функции, должны быть заданы перед выполнением оператора присваивания.

Например,

a := 3.5

f(x) := cos(x) + 5 a

g(x,u) := a f(x) + u(x)

s := g(3,sin)

Наиболее часто используемые функции пользователя можно, глобально определив, поместить в специальные файлы, например, USERLIB.MCD, и при необходимости включать их в начало или конец текущего документа.

Условия и функция if

• Простое условие.

• Составные условия.

• Формат функции if.

В MathCADе допустимы простые и составные условия.

Простое условие имеет вид:

выраж.1 условный_оператор выраж.2

Составные условия содержат простые, соединенные знаками логического умножения ( ) и логического сложения (+). Например, условие -4<x 56 можно записать следующим образом: (-4<x) (x 56), а совокупность условий -4<x 7, 12<x 34 так: (x>-4) (x 7)+(x 34) (x>12).

Условие принимает значение 0, если оно ложно, и 1 в случае его истинности.

Например,

x := 4 x > 7 = 0 x < 10 = 1

y := -1 (x > 7) (y < 0) = 0

(x > 7) + (y < 0) = 1

Формат функции: if ( условие, выраж.1, выраж.2 )

Если условие истинно, то функция if принимает значение выраж.1, иначе - выраж.2. Выражения, в свою очередь, могут содержать функцию if.

Замечание: Вместо условия можно указать любое выражение, и если оно принимает значения, отличные от 0, то функция if принимает значение выраж.1, иначе - значение выраж.2.

Например: если x=0, то функция if(x>4,cos(x),24) принимает значение 24, функция if(x<0,tan(x),if(x>5,cos(x),x+4)) —значение 4, а функция if(x+2,5,2+x) — значение 5.

Пусть требуется найти значение функции

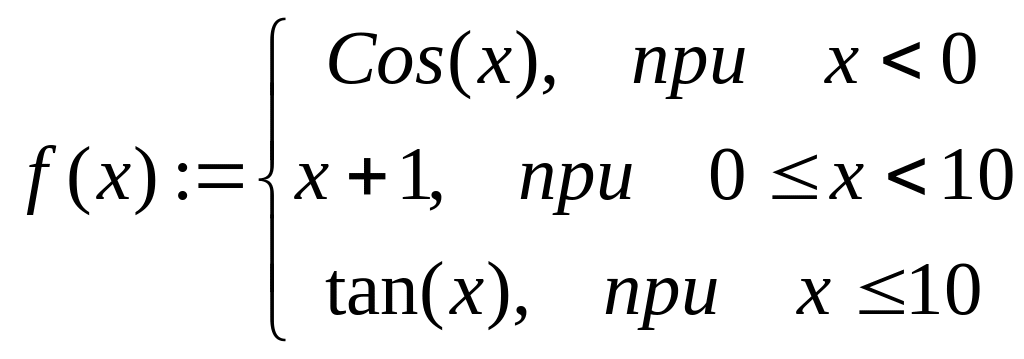для x=7.

MathCAD-документ может быть составлен следующим образом:

f(x):= if(x<0,cos(x),if(x<10,x+1,tan(x))) f(7)= 8

Замечание: Функция f(x) может быть задана и таким образом:

f(x):=(x<0) cos(x)+(x>0) (x<10) (x+1)+(x>10) tan(x).

Переменные диапазона (ранжированные переменные)

Переменные диапазона - это переменные, которые принимают серию значений из заданного диапазона при каждом их использовании.

С помощью переменных диапазона вы можете выполнить цикл - многократно вычислить одно и то же выражение для различных значений переменной из диапазона. Результаты вычисления могут быть записаны в массив MathCAD и отображены в виде вектора (матрицы), таблицы или графика.

Переменная диапазона задается следующим образом:

имя_переменной := выраж.1..выраж.N или

имя_переменной := выраж.1,выраж.2..выраж.N

Здесь выраж.1 - начальное значение переменной, выраж.2 - второе значение переменной, выраж.N - последнее значение переменной, разность выраж.2-выраж.1 задает шаг изменения переменной.

Если выраж.2 не задано (первая форма задания диапазона), то шаг принимается равным 1.

Заметим, что все входящие в выраж.1, выраж.2, выраж.N параметры должны быть определены до задания диапазона.

Ввод символа ".." осуществляется с помощью клавиши ";" (точка с запятой).

Например, x:1.5;40.56 выглядит как x:=1.5..40.56.

Теперь переменная x будет меняться от 1.5 с шагом 1 до тех пор, пока не превысит значение 40.56.

Пример MathCAD-документа:

x0 := -1.4 h := 0.5 xk := 5.5 x := x0,x0+h .. xk

f(x) := sin(x)

З амечание: последнее присваивание выполняется столько раз, каково значение выражения:

Целая часть

Переменные-индексы

Переменные, предназначенные для организации циклических и итерационных процессов, задания индексированных переменных, называются переменными-индексами или индексными переменными.

При задании диапазона изменения переменной-индекса выраж.1, выраж.2, выраж.N должны быть выражениями целого типа.

Например:

Ввод	Как выглядит
k:1;40	k:=1..40
j:1,3;40	j:=1,3..40

Теперь индекс k будет меняться от 1 до 40 каждый раз, когда вы будете использовать его в равенстве. Индекс j будет меняться от 1 до 39 с шагом 2.

Индексная переменная в операторах суммирования и произведения необязательно является целочисленной.