
- •Федеральное государственное образовательное бюджетное учреждение высшего профессионального образования «Поволжский государственный университет телекоммуникаций и информатики»
- •Конспект лекций
- •Содержание конспекта лекций
- •Понятие информатики
- •Информация, ее представление и измерение Понятие и характерные черты информации
- •Преобразование сообщений
- •Рассмотрим более подробно преобразования одного сигнала в другой.
- •Преобразование д®н
- •Лекция 2 Меры информации
- •Объем информации V (объемный подход)
- •Комбинаторная мера
- •Двоичная логарифмическая мера
- •Вероятностная мера
- •Понятия бита, байта
- •Представление информации в эвм Кодирование информации
- •Представление символьной информации
- •Краткая информация о других системах кодирования.
- •Универсальная система кодирования текстовых данных
- •Лекция 3 Представление и обработка чисел в компьютере Системы счисления и коды, применяемые в вычислительной технике
- •Перевод из одной системы счисления в другую.
- •Двоичная система счисления (в)
- •Восьмеричная система счисления (о)
- •Шестнадцатиричная система счисления (h)
- •Информационно–логические основы построения эвм Формы представления чисел
- •Операции над двоично-десятичными числами в упакованном формате без учета знака
- •Лекция 4 Логические основы построения эвм
- •Лекция 5 Технические средства реализации информационных процессов Краткая история вычислительной техники
- •Классическая архитектура эвм
- •Магистрально-модульный принцип построения компьютера
- •Лекция 6 Программное обеспечение эвм
- •Операционные системы
- •Лекция 7 Модели решения функциональных и вычислительных задач
- •Что такое модель?
- •Классификация моделей. Материальные и информационные модели
- •1. Область использования
- •2. Учет фактора времени и области использования
- •3. Классификация по способу представления
- •Этапы моделирования
- •Алгоритмизация и основные этапы решения инженерных задач
- •Технология решения задач на компьютере Этапы решения задач на компьютере
- •Основы структурного программирования Алгоритмы
- •Базовые алгоритмические структуры
- •Линейные алгоритмы
- •Пример алгоритма линейной структуры.
- •Пример алгоритма ветвления.
- •Модульное программирование
- •Объектно-ориентированное программирование
- •Языки программирования, их классификация
- •Транслятор, компилятор, интерпретатор
- •Контрольные вопросы:
- •Лекция 8 Технология обработки текстовой информации
- •Возможности текстовых процессоров
- •Форматирование текста Приемы форматирования текста
- •Задание параметров шрифта
- •Форматирование абзацев
- •Выделение текста с помощью мыши
- •Создание таблиц и работа с таблицами в текстовом редакторе
- •Структура таблицы
- •Создание оглавления средствами текстового процессора
- •Использование стилей заголовков
- •Лекция 9 Технология обработки графической информации Кодирование графической информации
- •Цветовые модели.
- •Векторное и фрактальное изображения.
- •Преобразование файлов из одного формата в другой
- •Преобразование файлов из растрового формата в векторный
- •Преобразование файлов одного векторного формата в другой
- •Лекция 10 Технология обработки числовой информации, табличный процессор
- •Мультимедиа технологии. Компьютерные презентации с использованием мультимедиа технологии
- •Начало работы
- •6.2. Создание мультимедийных презентаций. Настройка параметров демонстрации п Рис. 1. Выбор разметки слайда ервая презентация
- •Оформление слайда
- •Дополнительные объекты
- •Анимация
- •Показ слайдов
- •Лекция 11 Сжатие информации
- •1 Основные понятия баз данных
- •Определение основных терминов
- •Основные требования, предъявляемые к банкам данных
- •Компоненты банка данных
- •Пользователи бд и субд
- •2 Классификация бд
- •Классификация баз данных
- •Классификация субд
- •Основные функции субд
- •1. Непосредственное управление данными во внешней памяти
- •2. Управление буферами оперативной памяти
- •3. Управление транзакциями
- •4. Журнализация
- •5. Поддержка языков бд
- •Функциональные возможности субд
- •3 Проектирование баз данных Подходы к проектированию
- •Архитектура субд
- •Методология проектирования баз данных
- •Основные этапы разработки бд
- •4 Модели организации баз данных
- •Иерархическая модель базы данных
- •Сетевая модель базы данных.
- •Операции над данными в сетевой модели бд.
- •Достоинства и недостатки ранних субд
- •Объектно-ориентированные субд
- •Объектно-реляционные субд
- •5 Реляционный подход к построению инфологической модели Реляционная модель данных
- •Понятие информационного объекта
- •Нормализация отношений
- •Свойства отношений.
- •Простые и составные ключи
- •6. Работа с субд ms Access Объекты Microsoft Access.
- •Работа с таблицами
- •Создание межтабличных связей
- •Работа с запросами
- •Запросы и фильтры
- •Работа с формами
- •Работа с отчётами
- •Программные системы в научных исследованиях, использование пакетов математических и инженерных расчетов Система MathCad (Mathematical Computer Aided Design)
- •MathCad-документ и его структура
- •Элементарные математические встроенные функции
- •Функции, определяемые пользователем
- •Условия и функция if
- •Индексированные переменные и итерация
- •К ак выглядит
- •Аргументы:
- •Аргументы:
- •Аргументы:
Перевод из одной системы счисления в другую.
Для целой части используется правило последовательного деления
Для дробной части правило последовательного умножения.
Правило перевода целой части — правило последовательного деления:
Для перевода целой части числа из С.С. с основанием p в С.С. с основанием q необходимо разделить целую часть заданного числа и получаемое частное на основание системы в которую необходимо преобразовать данное число, представленное в С.С. p, до тех пор пока частное не станет меньше q.
Старшей цифрой записи числа служит последнее частное, а следующие за ней дают остатки от деления частичных частных. Выписываются в порядке обратном их получения.
таким образом, получили число: (последнее частное) и затем остатки в порядке обратном их получения.
Двоичная система счисления (в)
Пример 12.
преобразовать десятичное число 134 в двоичное:
|
134 |
67 |
33 |
16 |
8 |
4 |
2 |
1 |
Последнее частное |
Остатки |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
|
Получили число10000110
Правило перевода дробной части — правило последовательного умножения:
Для перевода правильной дроби из С.С. с основанием p в С.С. с основанием q необходимо умножить исходную дробь и дробные части получающихся произведений на основание системы в которую необходимо преобразовать данное число, представленное в С.С. p. Целые части получающихся произведений дают последовательность цифр представления дроби в С.С. q.
Пример 13.
преобразовать десятичную дробь 0.375 в двоичную
0.375 * 2 = 0.75 0 Старший Значащий Разряд(СЗР)
0.75 * 2 = 1.5 1
0.5 *2 = 1 1 Младший ЗР (МЗР)
Результат 0.011
Выполнение арифметических действий в двоичной системе счисления
Таблица в двоичной системе счисления |
|
Сложения |
Умножения |
0 + 0 = 0 0 + 1 = 1 1 + 0 = 1 1 + 1 = 10 |
0 х 0 = 0 0 х 1 = 0 1 х 0 = 0 1 х 1 = 1 |
Восьмеричная система счисления (о)
Восьмеричная система счисления имеет основание 8. В ней используются следующие символы: 0, 1, 2, 3, 4, 5, 6, 7. Восьмеричная система применяется для удобства записи чисел. Поскольку 23 = 8, то каждый восьмеричный символ (0 до 7) может быть представлен 3-х битовым числом (000 …..111)
Для перевода двоичного числа в восьмеричную систему счисления необходимо двоичное число разбить вправо и влево от запятой на триады (по три двоичных бита). При необходимости крайнюю левую триаду (целой части) и крайнюю правую (дробной части) дополняют нулями, затем каждую триаду заменяют восьмеричным числом.
Пример.
Представить восьмеричным эквивалентом число: 10101011111101 ( B )=>25375 (О )
Двоичный код, разбитый на триады |
010 добавлен 0 |
101 |
011 |
111 |
101 |
Восьмеричный код |
2 |
5 |
3 |
7 |
5 |
Для перевода из восьмеричной в двоичную с.с. достаточно заменить каждую цифру восьмеричного числа соответствующим 3-х разрядным двоичным числом. При этом незначащие нули слева от целой части числа, и справа от дробной части отбрасываются.
Пример.
Представить двоичным эквивалентом число: 375,75 ( O )=>11111101,1111 ( B )
Восьмеричный код |
3 |
7 |
5, |
7 |
5 |
Двоичный |
011 |
111 |
101, |
111 |
101 |
Таблица сложения в восьмеричной системе счисления
+ |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
0 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
1 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
10 |
2 |
2 |
3 |
4 |
5 |
6 |
7 |
10 |
11 |
3 |
3 |
4 |
5 |
6 |
7 |
10 |
11 |
12 |
4 |
4 |
5 |
6 |
7 |
10 |
11 |
12 |
13 |
5 |
5 |
6 |
7 |
10 |
11 |
12 |
13 |
14 |
6 |
6 |
7 |
10 |
11 |
12 |
13 |
14 |
15 |
7 |
7 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
Таблица умножения для восьмеричной системы счисления
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
2 |
0 |
2 |
4 |
6 |
10 |
12 |
14 |
16 |
3 |
0 |
3 |
6 |
11 |
14 |
17 |
22 |
25 |
4 |
0 |
4 |
10 |
14 |
20 |
24 |
30 |
34 |
5 |
0 |
5 |
12 |
17 |
24 |
31 |
36 |
43 |
6 |
0 |
6 |
14 |
22 |
30 |
36 |
44 |
52 |
7 |
0 |
7 |
16 |
25 |
34 |
43 |
52 |
61 |

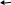 Частичные
частные
Частичные
частные