Универсальная система кодирования текстовых данных

Если проанализировать организационные трудности, связанные с созданием единой системы кодирования текстовых данных, то можно прийти к выводу, что они вызваны ограниченным набором кодов (256). В то же время, очевидно, что если, например, кодировать символы не восьмиразрядными двоичными числами, а числами с большим количеством разрядов, то и диапазон возможных значений кодов станет намного больше. Такая система, основанная на 16-разрядном кодировании символов, получила название универсальной Unicode. Шестнадцать разрядов позволяют обеспечить уникальные коды для 65536 различных символов – этого поля достаточно для размещения в одной таблице символов большинства языков планеты.

Сегодня наблюдается постепенный переход документов и программных средств на универсальную систему кодирования.

Таким образом в интерпретации файла в формате Unicode каждые два байта интерпретируется как изображаемый символ. как и в других кодировках кроме кодов изображаемых символов, файл в формате Unicode включат ряд управляющих кодов, например, перевода строки, конца файла. и др.

Контрольные вопросы:

1. Три уровня проблем передачи информации.

2. Вероятностный и объемный поход к измерению количества информации.

3. Понятие энтропии.

4. Меры информации

5. Объем информации V (объемный подход).

6. Количество информации / (энтропийный/вероятностный подход)

7. Кодирование символьной информации. Математическая постановка задачи кодирования.

8. Равномерное алфавитное кодирование. Преставление символьной информации в компьютере. Системы кодирования.

Лекция 3 Представление и обработка чисел в компьютере Системы счисления и коды, применяемые в вычислительной технике

Представление данных в компьютере определяет не только способ их записи, но и допустимый набор операций над ними.

1. числа записываются в двоичной системе счисления

2. для записи и обработки чисел отводится конечное количество разрядов

Замечания относительно понятия ЧИСЛО. Оно имеет ЗНАЧЕНИЕ и ФОРМУ ПРЕСТАВЛЕНИЯ. Последняя определяет порядок записи числа с помощью предназначенных ля этого знаков. При этом ЗНАЧЕНИЕ является инвариантом, то есть не зависит от способа его представления. То есть отсутствует взаимно однозначное соответствие между представлением числа и его значением, всякое значение числа может быть записано по-разному. Поэтому вопрос- каковы формы представления чисел. и можно ли переходить от одной к другой.

Системой счисления (с.с.) называется способ представления чисел посредством цифровых знаков. В качестве цифровых знаков используются арабские и римские цифры.

В любой системе счисления для представления чисел выбираются некоторые базовые символы (цифры), и все числа получаются в результате строго определенных операций над ними. Число таких базовых символов называется основанием системы счисления.

Существует два известных типа систем счисления: непозиционные и позиционные.

В непозиционных системах счисления каждая цифра имеет одно и тоже значение независимо от положения в записи числа (значение знака не зависит от того места, которое он занимает в числе).

Непозиционной системой счисления является самая простая система с одним символом (палочкой). Для изображения какого-либо числа в этой системе надо записать количество палочек, рав­ное данному числу. Например, запись числа 12 в такой системе счисления будет иметь вид: 111111111111, где каждая «палочка» обозначена символом 1. Эта система неэффективна, так как фор­ма записи очень громоздка.

Примером непозиционных с.с. может служить римская или латинская с.с. Она включает в себя следующие цифровые обозначения: 1 – I; 2-II; 3-III; 4-IV; 5-V; …; 10-X;…; 50-L; 100-C; 1000-M и т.д.

Пример.

Записать числа 114; 155; 1999 римскими цифрами:

114 — CXIV; 155 — CLV; 1999 — MCMXCIX.

В виду сложности не нашла своего применения в математике.

В позиционной с.с. с основанием p числа представляются в виде последовательности цифровых знаков:

N=(a_na_n-1a_n-2… a₂a₁ a₀, a_-1 a_-2 a_-3)_p

Основание системы счисления – это количество цифр используемых для формирования данной системы счисления.

В зависимости от основания системы счисления различают:

• десятичную с.с. (0, 1, 2, 3, 4, 5, 6, 7, 8, 9);

• двоичную с.с. (0, 1);

• восьмеричную (0, 1, 2, 3, 4, 5, 6, 7);

• шестнадцатеричную (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F) .

В этих системах значение цифры определяется местом (позицией), где она стоит в числе

Пример.

6321(10) =6 3 2 1=6*10³+3*10²+2*10+1

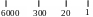
каждую позицию цифры в числе принято оценивать «весом» показателем степени системы счисления. В первой справа пози­ции размещаются единицы (для целого числа), в соседней с ней второй позиции – десятки, в третьей – сотни, в четвертой - тысячи и т.д. Дробная часть десятичного числа находится справа от десятичной точки, используемой для отделения целой части числа от дробной. Каждая позиция справа от десятичной точки имеет свой вес (10^-1, 10^-2 и т.д).

В любой позиционной с.с. число может быть записано через полином (многочлен):

а_т-1Р ^т-1+а_т-гР ^m-1+...+а₁Р ^-1+а₀Р ⁰+а_-1Р ^-1+а_-2Р ^-2+...+a_-sP ^-s, (1)

где нижние индексы определяют местоположение цифры в числе (разряд):

• положительные значения индексов — для целой части числа (т разрядов);

• отрицательные значения — для дробной (s разрядов).

Пример.

237,71(10) = 2*10²+3*10¹+7*10⁰+7*10^-1+1*10^-2

Двоичная система счисления имеет основание Р = 2 и использует для представле­ния информации всего две цифры: 0 и 1.

Существуют правила перевода чисел из одной сис­темы счисления в другую, основанные, в том числе и на соотноше­нии (1).

Пример

101110,101(2) =

1•25+0•24+1•23+1•22+1•21+0•20+1•2-1+0•2-2+1•2-3= 46,625(10),

т.е. двоичное число 101110,101 равно десятичному числу 46,625. При записи числа в десятичной системе счисления каждая позиция занята десятичной цифрой. Аналогично при записи двоичного числа каждая позиция занята двоичной циф­рой, называемой битом. Часто используется термин –наименьший значащий бит (крайний справа) и наибольший значащий бит (крайний слева).

Преобразование двоичных чисел в десятичные.

При работе ЭВМ часто бывает необходимо заменить двоичные числа их десятичными эквивалентами.

Процедура преобразования двоичного числа в десятичное проста: необходимо сложить десятичные веса всех разрядов двоичного числа, в которых содержаться единицы.

Пример 11.

Преобразование вещественного двоичного числа : 101.011 в десятичное:

1. 0 1. 0 1 1 = 1*2² +0* 2¹+1* 2⁰+0* 2^-1+ 1*2^-2+1*2^-3 =5.375(10)