Задание 2 по разделу "Аналитическая геометрия"

Задача 1. Найти координаты и проверить коллинеарность векторов и , построенных на векторах и , если .

Решение.

1. Найдем координаты векторов и , выполняя линейные операции с векторами в координатной форме:

= ;

= .

2. Условием коллинеарности векторов и является пропорциональность их координат т.е.:

║ (9)

Проверим условие коллинеарности для векторов и :

║ .

Координаты векторов пропорциональны, следовательно, векторы коллинеарны.

Убедиться в том, что векторы коллинеарны можно следующим образом: по условию

,

т.е. выполняется условие , где = 2, следовательно ║ .

Ответ: векторы коллинеарны.

Задача 2. Найти косинус угла между векторами и , если даны координаты точек: А (– 1; 2; – 3); В (3; 4; – 6); С (1; 1; – 1).

Решение

Косинус угла между векторами и найдем по формуле

, (10)

где - скалярное произведение векторов;

- модули векторов.

Скалярное произведение векторов и может быть вычислено по формуле:

, (11)

где - координаты вектора ; - координаты вектора .

Модуль вектора равен корню квадратному из суммы квадратов его координат, т.е.:

. (12)

1. Вычислим координаты векторов. Если вектор задан координатами его конца (точка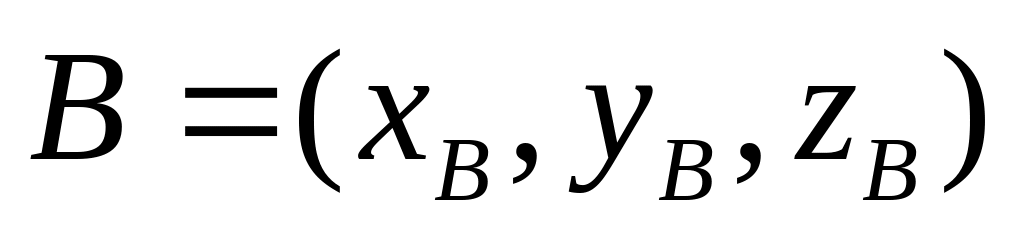 ) и начала (точка ), то координаты вектора определяются выражением:

, (13)

в соответствии с которым

;

.

Найдем модули векторов и по формуле (12):

; .

Вычислим скалярное произведение векторов (формула (11)):

.

Подставим найденные значения в формулу (10) и вычислим косинус угла между векторами и :

.

Ответ: 0.

Задача 3. Вычислить площадь параллелограмма, построенного на векторах и , если:

1) ;

2) .

Решение

Площадь параллелограмма, построенного на векторах и , может быть вычислена как модуль векторного произведения :

. (14)

По определению векторного произведения

, (15)

где φ – угол между векторами.

Если векторы и заданы своими координатами

= и = ,

то векторное произведение может быть вычислено с помощью определителя

. (16)

1). .

Векторы заданы своими координатами: и , поэтому для вычисления векторного произведения используем формулу (16), подставив в нее координаты векторов:

= =

= .

Найдем площадь параллелограмма (формула (14)), вычислив модуль вектора по формуле (12):

.

2). .

В данном случае вычислим векторное произведение , используя свойства векторного произведения:

.

Так как , , , получим

.

Найдем площадь параллелограмма (формула (14)), вычислив модуль векторного произведения по формуле (15): . В итоге получим:

Ответ: 1) ; 2) .

Задача 4.

а) Составить уравнение стороны АС треугольника, если точки А(– 3; 4) и В(2, 3) – его вершины, а М (1, 1) – точка пересечения его высот.

Решение

1. Уравнение прямой, проходящей через две данные точки и , имеет вид:

. (17)

Составим уравнение прямой ВМ как уравнение прямой, проходящей через две заданные точки В(2, 3) и М(1, 1), подставляя в уравнение (17) координаты точек B и М:

.

2. Уравнение прямой, проходящей через заданную точку перпендикулярно данной прямой , имеет вид:

. (18)

Воспользуемся уравнением (18) и составим уравнение прямой АС как уравнение прямой, проходящей через заданную точку А(– 3; 4) перпендикулярно прямой ВМ, уравнение которой: .:

.

Полученное уравнение может быть проверено.

Во-первых, можно проверить, проходит ли полученная прямая через точку А. Для этого достаточно подставить координаты точки А (– 3; 4) в полученное уравнение прямой АС и убедиться в том, что координаты точки А удовлетворяют этому уравнению: .

Во-вторых, можно проверить, выполняется ли условие перпендикулярности прямых АС и BM.

Условие перпендикулярности прямых, заданных общими уравнениями вида , имеет вид:

, (19)

т.е. условием перпендикулярности прямых является равенство нулю суммы произведений коэффициентов при переменных в уравнениях прямых.

Убедимся в перпендикулярности прямой АС: и прямой BM: , подставляя в условие (19) соответствующие коэффициенты: .

Ответ: .

б) Составить уравнение прямой, проходящей через точку С, которая делит отрезок МК в отношении 1:3, параллельно прямой , если М (-3; 4), К (11,0).

Решение

1. Координаты точки С, которая делит отрезок М₁М₂ в данном отношении λ, определяются формулами:

; (20)

где - координаты точки М₁- начала отрезка; - координаты точки М₂ –конца отрезка.

В нашем случае λ = 1/3, = (- 3,4); = (11,0). Подставляя эти значения в формулу (20), определим координаты точки С:

; .

Итак, точка С имеет координаты (1/2, 3).

2. Уравнение прямой, проходящей через заданную точку параллельно данной прямой , имеет вид:

. (21)

С помощью уравнения (21) составим уравнение прямой, проходящей через точку С(1/2, 3) параллельно прямой :

, или , или .

3. Условием параллельности прямых, является пропорциональность коэффициентов при переменных в общих уравнениях прямых, т.е.:

(22)

Проверим, выполняется ли условие параллельности (22) для прямых и : .

Ответ: .

в) В треугольнике с вершинами А(-2; 0), В(2; 6) и С(4; 2) найти уравнение стороны АС, медианы ВЕ и высоты ВD.

Решение

1. Составим уравнение прямой АС как уравнение прямой, проходящей через две заданные точки А(-2; 0), и С(4; 2) подставляя в уравнение (17) координаты точек А и С:

.

2. Воспользуемся уравнением (18) и составим уравнение прямой BD как уравнение прямой, проходящей через заданную точку В(2; 6) перпендикулярно прямой AC, уравнение которой 0:

.

3. Определим координаты точки Е, как координаты середины отрезка АС. Формула для определения координат середины отрезка может быть получена из формулы (20) при λ = 1:

; , (20)

где , - координаты точки А - начала отрезка; - координаты точки С – конца отрезка.

Подставляя в (20) координаты точек А(-2; 0) и С(4; 2), вычислим координаты точки Е:

; , т.е. Е(1,1)

4. Составим уравнение медианы BE как уравнение прямой, проходящей через две заданные точки В(2; 6), и Е(1,1) подставляя в уравнение (17) координаты точек B и E:

.

Ответ: x – 3y + 2 = 0; 5x – y –4 =0; 3x + y – 12 = 0.

Задача 5.

а) В эллипс вписана окружность , пересекающая большую ось в фокусах, лежащих на оси OY. Составить уравнение эллипса. Сделать чертеж.

Решение

1. Сделаем чертеж (см. рис.1).

Рис.1. Чертеж к задаче 5а.

2. Уравнение описывает окружность с центром в начале координат, радиус которой .

3. По условию задачи фокусы эллипса лежат на оси OY, тогда малая полуось эллипса лежит на оси ОХ и равна радиусу вписанной окружности, т.е. .

4. Окружность пересекает большую ось в фокусах эллипса, тогда фокусное расстояние равно радиусу окружности .

5. Найдем (квадрат большой полуоси эллипса) из соотношения :

.

6. Составим уравнение эллипса, воспользовавшись каноническим уравнением эллипса:

, (23)

Подставляя в уравнение (23) = 9, =18, получим:

.

Ответ: .

б) Составить уравнение окружности с центром в одной из вершин эллипса и проходящей через фокус параболы . Сделать чертеж.

Решение

1. Определим параметры и построим эллипс, описываемый уравнением . Сравнивая данное уравнение с каноническим уравнением эллипса (23) найдем:

; - полуоси эллипса.

Определим вершины эллипса как точки пересечения эллипса с осями координат: A₁(-3,0), A₂(3,0), B₁(0,5), B₂(0,-5) (см. рис.2).

Рис. 2. Чертеж к задаче 5б.

2. По уравнению параболы определим параметры и построим кривую.

Каноническое уравнение параболы имеет вид:

(24)

где p – параметр параболы.

Записывая уравнение в виде , и сравнивая полученное уравнение с каноническим уравнением (24), определим параметр параболы: .

Парабола, описываемая уравнением (24), проходит через начало координат (точка (0,0) – вершина параболы) и лежит в нижней полуплоскости (y ≤ 0).

Фокус параболы (24) - точка F с координатами (0, )., следовательно, фокусом параболы является точка F(0,-3).

3. Каноническое уравнение окружности радиуса R с центром в точке С( ) имеет вид:

. (25)

По условию задачи центр окружности лежит в одной из вершин эллипса. Выберем центр окружности в вершине эллипса B₂(0,-5), тогда координаты центра окружности , а радиус окружности . Подставляя полученные данные в (25), получим искомое каноническое уравнение окружности:

.

Ответ: x² + (y +5)² = 4.

в) Составить уравнение гиперболы, фокусы которой расположены на оси OY симметрично относительно начала координат, зная, что расстояние между фокусами равно 10, а угол между асимптотами кривой равен 60⁰. Сделать чертеж.

Решение

1. Каноническое уравнение гиперболы, фокусы которой расположены на оси OY симметрично относительно начала координат, имеет вид:

, (26)

где и b – вещественная и мнимая полуоси гиперболы соответственно, которые в данной задаче являются неизвестными (чертеж см. на рис.3).

Рис. 3. Чертеж к задаче 5в.

2. Для нахождения двух неизвестных составим систему из двух уравнений.

Для гиперболы

, (27)

где с – фокусное расстояние.

По условию задачи 2с = 10, с = 5, тогда из (27) получим первое уравнение:

.

Обозначим угол между асимптотами α. По условию задачи α = 60⁰. Рассматривая главный прямоугольник гиперболы, найдем тангенс угла α/2:

, или , откуда получим второе уравнение системы

.

3. Решая систему, получим:

.

Подставляя найденные значения в уравнение (26), получим искомое уравнение гиперболы:

или 4y² – 12x² = 75.

Ответ: 4y² – 12x² = 75.

Задача 6. Написать разложение вектора x по базису p, q, r, если x = (2, –1, 1)

p = (1; 1; 1), q = (0; 2;3), r = (0; 1;5).

Решение²

1. Пусть - координаты вектора x в новом базисе, тогда разложение вектора по базису p, q, r будет иметь вид:

(28)

Подставим в векторное равенство (28) координаты векторов:

.

Выполним линейные операции с векторами в левой части равенства:

.

Если векторы равны, то равны и их соответствующие координаты. Приравнивая соответствующие координаты векторов, стоящих в левой и правой части равенства, получим систему линейных уравнений:

.

2. Найдем решение системы, используя метод Гаусса (система может быть решена и методом Крамера). Составим расширенную матрицу системы и приедем ее к трапециевидной форме:

По виду трапециевидной матрицы заключаем, что система совместна и имеет единственное решение. Найдем значения неизвестных, решая укороченную треугольную систему:

.

Подставив найденные координаты вектора в (28), получим искомое разложение вектора по базису p, q, r.

Ответ: x = 2p – 2q +r.