
- •Множини та операції над ними Лекція 2
- •1.1. Поняття множини
- •1.2. Основні означення Множини позначаються великими літерами латинського алфавіту. Порожню множину позначають символом , це множина, яка не має ні одного елемента.
- •6. Аксіома об’єднання. Для довільної множини a існує множина b , яка складається точно з усіх елементів, що входять до елементів множини a.
- •7. Аксіома булеана. Для будь-якої множини a існує іі булеан в(a) , тобто сукупність всіх підмножин множини a.
- •1.3. Способи визначення множини.
- •1.4. Операції над множинами.
- •1.5. Діаграми Ейлера – Венна
- •З цієї діаграми добре видно, що симетрична різниця визначається формулою . Алгебра множин. Закони алгебри множин.
- •1.6. Декартовий добуток.
1.4. Операції над множинами.
Отже,
множина
називається підмножиною
множини
(![]() ),
якщо всі елементи множини
є також елементами множини
(
),
якщо всі елементи множини
є також елементами множини
(![]() ).
В цьому разі множина
є надмножиною
множини
.
).
В цьому разі множина
є надмножиною
множини
.
Маючи на увазі ці означення, аксіому об’ємності можна коротко записати так:
![]() .
.
Приклади 1.4.
Множина
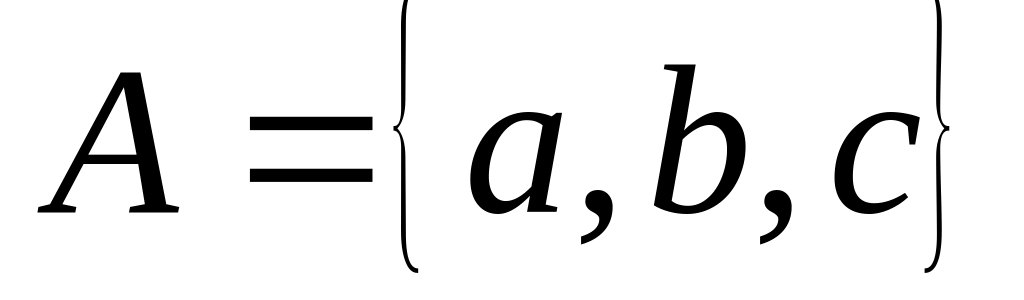 є власною підмножиною множини
є власною підмножиною множини
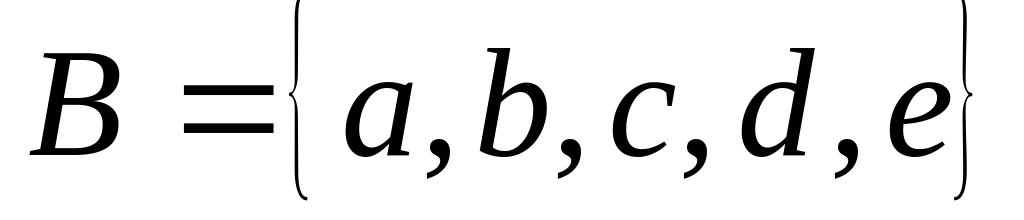 .
.Множина студентів ІНТ є власною підмножиною множини студентів НАУ.
Множина натуральних чисел є власною підмножиною множини цілих чисел.
Множина раціональних чисел є власною підмножиною дійсних чисел.
Нехай
є деякою множиною. Тоді позначення
![]() є множиною всіх підмножин множини
.
У цьому випадку множину
називають універсальною
(універсум),
а множину
–
множиною-степенем,
або булеаном
множини
.
є множиною всіх підмножин множини
.
У цьому випадку множину
називають універсальною
(універсум),
а множину
–
множиною-степенем,
або булеаном
множини
.
Приклад 1.5.
Нехай
![]() .
Тоді булеаном цієї множини буде множина
.
Тоді булеаном цієї множини буде множина
![]() .
Число елементів булеана можна розрахувати
за формулою
.
Число елементів булеана можна розрахувати
за формулою
![]() .
Для наведеного приклада
.
Для наведеного приклада
![]() .
У комп’ютері для кодуванна цифр, букв
і різних символів використовують 8
розрядів двійкового коду, що дає
.
У комп’ютері для кодуванна цифр, букв
і різних символів використовують 8
розрядів двійкового коду, що дає
![]() кодових комбінацій.
кодових комбінацій.
Об’єднанням множин і називається множина, яка складається з тих і тільки тих елементів, які входять до складу хоча б однієї з цих множин:
![]() .
.
Приклад 1.6.
Якщо
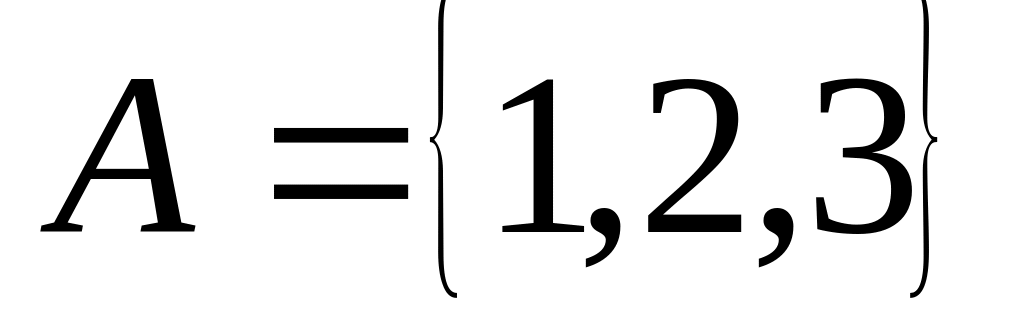 ,
,
 ,
то
,
то
 .
.Якщо
 –
множина парних натуральних чисел, а
–
множина парних натуральних чисел, а
 –
множина всіх непарних натуральних
чисел, то
–
множина всіх непарних натуральних
чисел, то –
це множина всіх натуральних чисел.
–
це множина всіх натуральних чисел.
Перетином
множин
і
називається множина, яка складається
з елементів, що входять до складу обох
множин:
![]() .
Якщо
.
Якщо
![]() ,
то множини
і
вважаються такими, що не перетинаються.
,
то множини
і
вважаються такими, що не перетинаються.
Приклад 1.7.
Якщо , , то
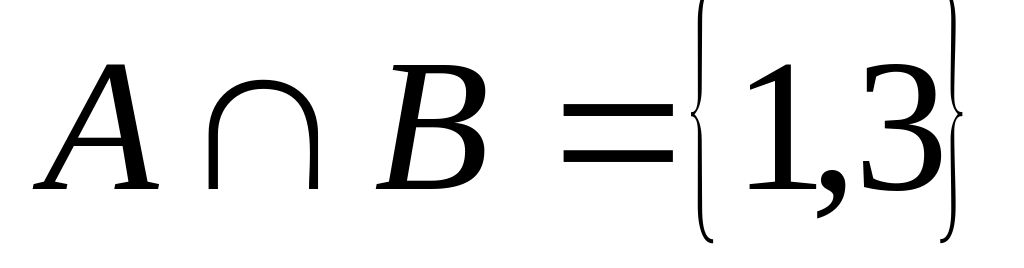 .
. .
. .
. .
.Якщо – множина прямих, які проходять через точку деякої площини, а – множина прямих, що проходять через точку
 цієї площини, то
цієї площини, то
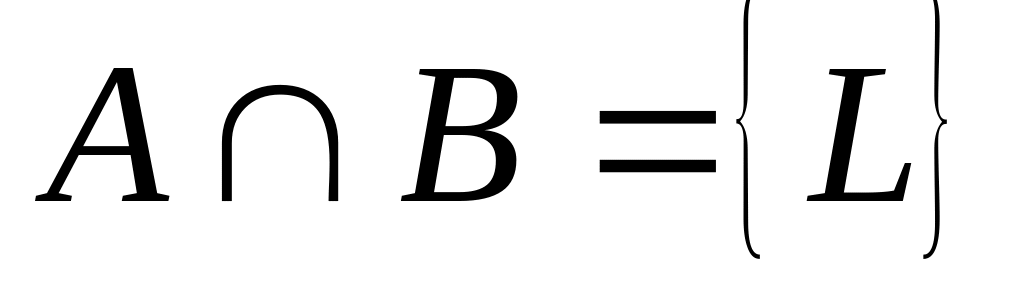 ,
де
,
де
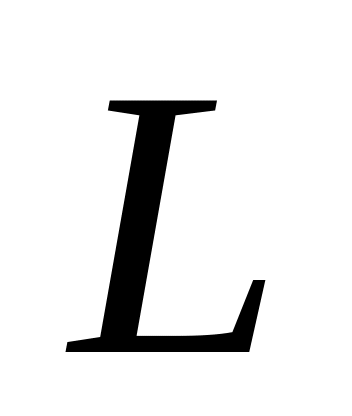 –
пряма, яка проходить через ці дві точки
і
.
–
пряма, яка проходить через ці дві точки
і
.
Якщо
множина
являє собою об’єднання підмножин
![]() ,
то сукупність підмножин
,
то сукупність підмножин
![]() називається
покриттям
множини
.
Якщо
ж сукупність підмножин така, що
називається
покриттям
множини
.
Якщо
ж сукупність підмножин така, що
![]() ,
то сукупність цих підмножин
називається розбиттям
множини
.
,
то сукупність цих підмножин
називається розбиттям
множини
.
Приклад 1.8.
Нехай – множина студентів НАУ, які його
закінчили,
а
![]() –
множини студентів, які закінчили
–
множини студентів, які закінчили
![]() -й
факультет. Припустимо, що серед цих
студентів є такі, що закінчили декілька
факультетів. Отже, є такі студенти, які
одночасно є елементами декількох множин,
тому сукупність підмножин
є
покриттям множини
,
оскільки вона є об’єднанням підмножин.
-й
факультет. Припустимо, що серед цих
студентів є такі, що закінчили декілька
факультетів. Отже, є такі студенти, які
одночасно є елементами декількох множин,
тому сукупність підмножин
є
покриттям множини
,
оскільки вона є об’єднанням підмножин.
Тепер припустимо, що множина студентів, які в даний момент вчаться на -му факультеті. Тобто в цьому разі кожний студент має бути лише на одному факультеті і, отже, множини не перетинаються, тобто . Таким чином, в цьому разі сукупність підмножин є розбиттям множини .
Різницею двох множин і називається підмножина
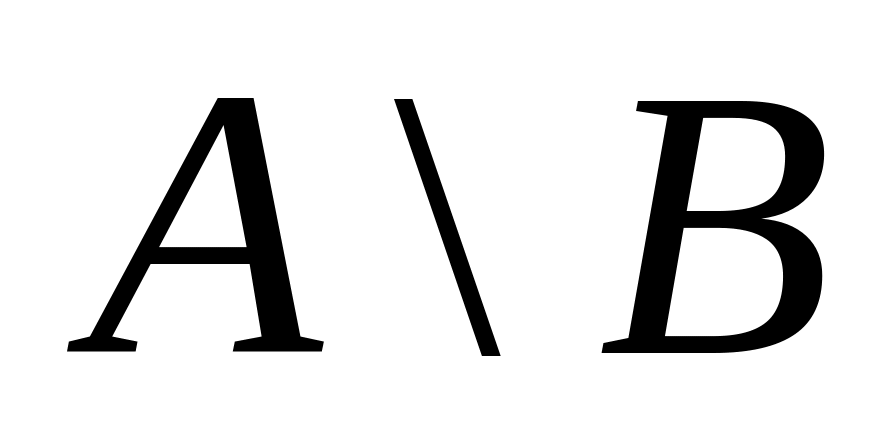 множини
,
яка складається з елементів множини
, що не входять в склад множини
:
множини
,
яка складається з елементів множини
, що не входять в склад множини
:
 (рис. 1):
(рис. 1):

Якщо
,
то підмножина
називається доповненням
множини
в множині
.
Доповнення позначають символом
![]() або
або
![]() .
.
Виконання
операції "різниця" тепер можна
реалізувати за допомогою основних
операцій перетину множини A
з доповненням множини B,
тобто С=(А\В)=(А![]() ).
).
Симетричною
різницею
множин
і
називається множина, яка є об'єднанням
двох різниць множин
![]() .
.
Оскільки
![]() ,
то цю формулу можна переписати:
,
то цю формулу можна переписати:
![]() .
.
Диз’юнктивна
сума
–
це множина, яка визначається за
властивістю:
![]() , вона
і є, власне, симетричною різницею.
, вона
і є, власне, симетричною різницею.
Слід
звернути особливу увагу на те, що
![]() і тоді симетричну різницю можна записати
формулою
і тоді симетричну різницю можна записати
формулою
![]() .
Якщо
симетрична
різниця двох множин є порожньою
.
Якщо
симетрична
різниця двох множин є порожньою
![]() ,
то А=В.
Це
правило часто використовується
при доведенні
тотожностей
теорії множин.
,
то А=В.
Це
правило часто використовується
при доведенні
тотожностей
теорії множин.
Приклад 1.9.
Нехай
![]() Тоді
Тоді
![]()
Якщо
–
довільна "універсальна" множина,
тобто така, що всі інші множини є
підмножинами цієї множини, то різниця
![]() називається
доповненням
множини
і позначається через
(іноді
називається
доповненням
множини
і позначається через
(іноді
![]() ).
Точніше, Доповненням
(запереченням) множини
A
(до універсальноі множини
).
Точніше, Доповненням
(запереченням) множини
A
(до універсальноі множини
![]() )
називається
множина
)
називається
множина
![]() .
Інакше кажучи д
.
Інакше кажучи д оповненням
множини А
є множина, яка складається із всіх тих
елементів, що належать універсальній
множині U
і не належать множині А, тобто
(рис.2):
оповненням
множини А
є множина, яка складається із всіх тих
елементів, що належать універсальній
множині U
і не належать множині А, тобто
(рис.2):
Приклад 1.10.
Нехай є
універсальна множина
![]() .
З неї можна виділити множини D
=
{-1 ,6 ,4}
, E
=
{-1,0 ,4 ,6 , 7} ,
F
=
. Тоді
доповненнями до цих множин будуть
.
З неї можна виділити множини D
=
{-1 ,6 ,4}
, E
=
{-1,0 ,4 ,6 , 7} ,
F
=
. Тоді
доповненнями до цих множин будуть
![]() = {-2 ,0 , 1 , 2 ,3 ,5 , 7} ,
= {-2 ,0 , 1 , 2 ,3 ,5 , 7} ,
![]() =
{-2 , 1 , 2 ,3 ,5} ,
=
{-2 , 1 , 2 ,3 ,5} ,
![]() .
.
Приклад 1.11.
Якщо
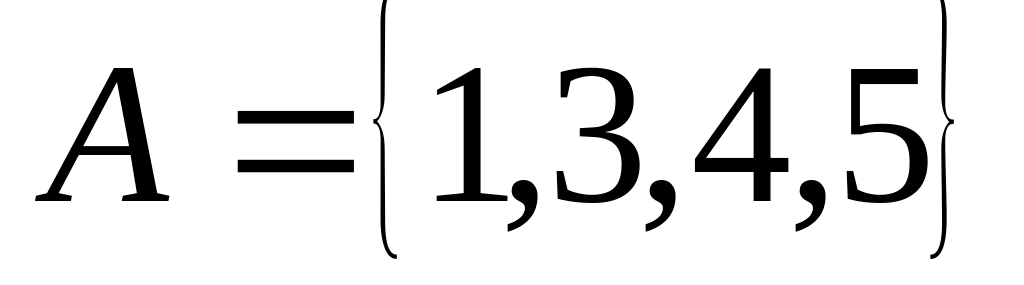 ,
,
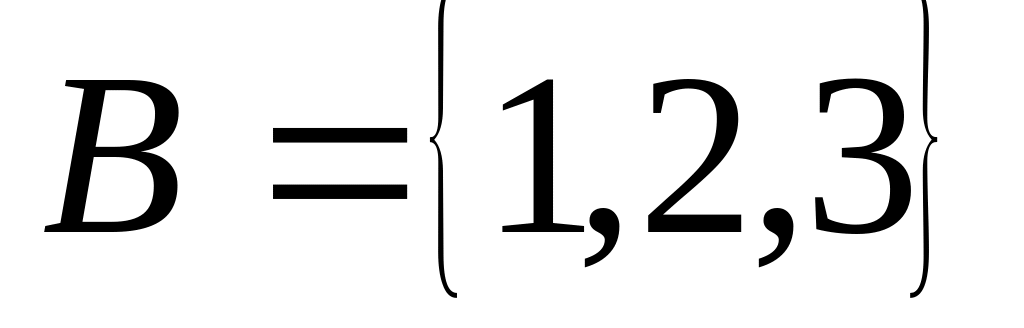 ,
то
,
то
 ,
то перетини множин
,
то перетини множин
![]()
Якщо
 ,
,
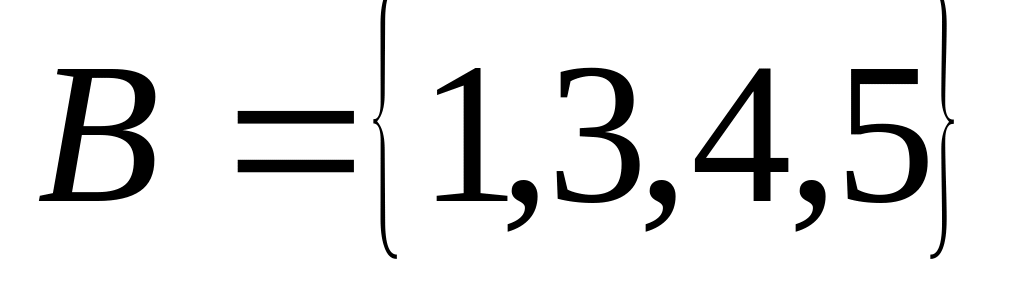 ,
то різниця цих множин
,
то різниця цих множин
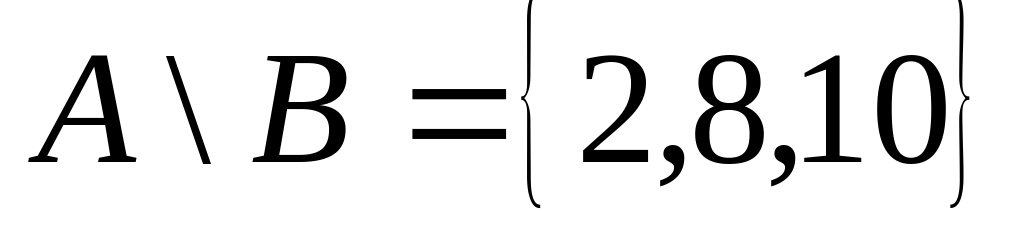 ,
а їх перетини
,
а їх перетини
![]()
![]()
3.
![]() .
.
