1.3. Частотная двоичная модуляция

При использовании частотной манипуляции несущего колебания для передачи элементарных сообщений «0» и «1» применяют такой разнос частот Δf в элементарных посылках U₁(t) и U₂(t), при котором коэффициент их взаимной корреляции равен или близок к нулю. В этом случае говорят об ортогональности или квазиортогональности сигналов U₁(t) и U₂(t), имеющих одинаковые длительности t_и и соответствующие частоты заполнения радиоимпульсов f₁ и f₂.

При равных амплитудах U_m сигналов U₁(t) и U₂(t) функция их взаимной корреляции

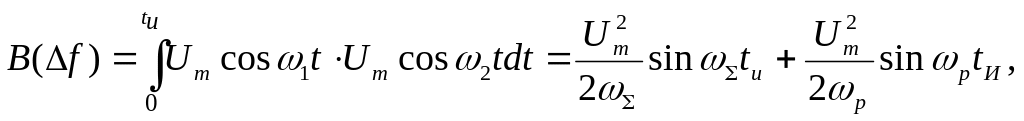
где

.

Умножая и деля оба слагаемых на t_и получаем

.

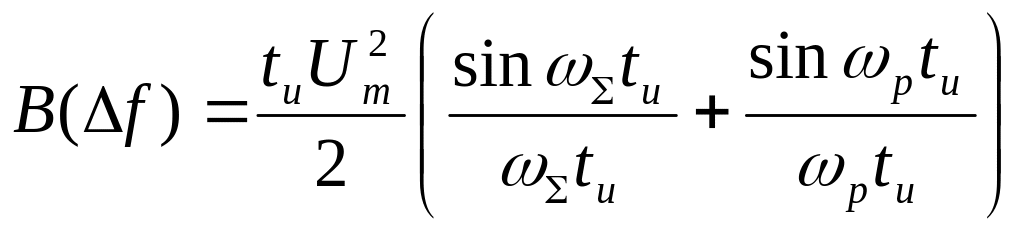В реальных системах связи ω_р<<ω_Σ, поэтому, пренебрегая малыми значениями первого слагаемого в скобках и нормируя по максимальному значению функцию автокорреляции, получаем коэффициент корреляции

.

Его значения будут равны нулю при аргументе синуса , где к = 1,2,3…, то есть при значениях

.

При таких значениях Δf сигналы U₁(t) и U₂(t) будут строго ортогональны.

Квазиортогональными сигналами будут такие, у которых r не равен нулю, но достаточно мал. Например, при нецелом значении к = 3,5

r(Δf ) = sin (кπ)/ (кπ) = sin(3,5π)/( 3,5π) ≈ -0,091.

При к=1, Δf=1/2 t_и. Такие сигналы называют сигналами с минимальным частотным сдвигом.

Будем считать сигналы U₁(t) и U₂(t) ортогональными, характеризуемыми в их аддитивной смеси с тепловым шумом соответствующими функциями правдоподобия

Отношение правдоподобия при одинаковых энергиях сигналов Е₁ =Е₂ = Е

Как указывалось выше, при использовании в качестве критерия распознавания критерия максимального правдоподобия

Λ₀ = 1,

и правило распознавания сигналов U₁(t) и U₂(t) принимает следующую форму

То есть оптимальный приемник должен вычислять корреляционные интегралы

,

,

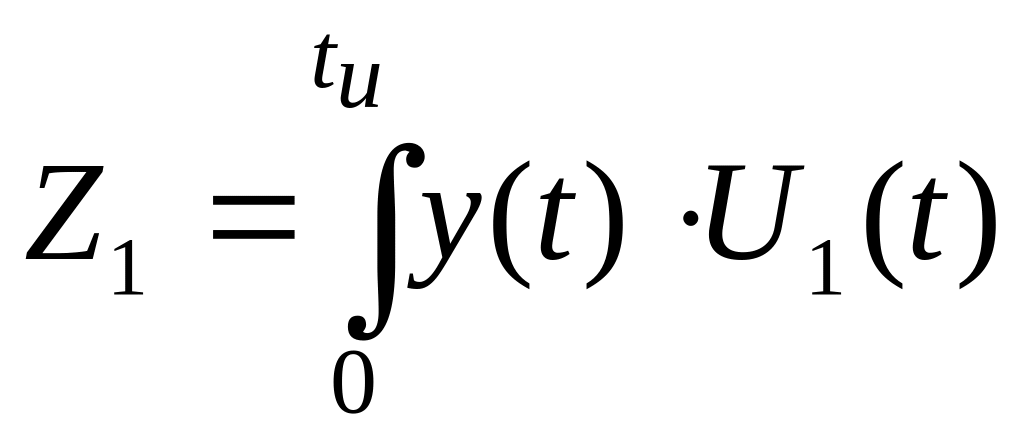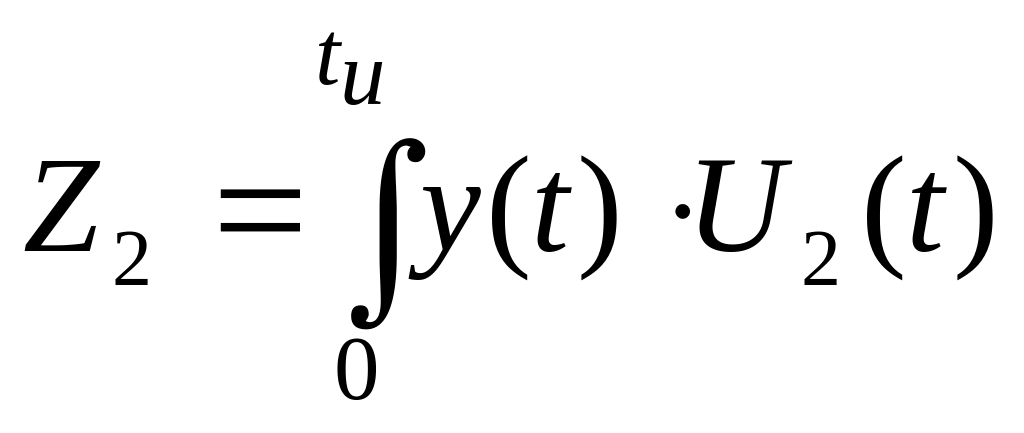образовывать их разность и сравнивать ее с нулевым порогом. Если разность (Z₁-Z₂) положительна, принимается решение о приеме сигнала U₁(t) и соответствующего элементарного сообщения «1». В противном случае считается принятым сигнал U₂(t) и соответствующее элементарное сообщение «0».

При этом в приемнике должны храниться и вовремя подаваться на перемножитель копии сигналов U₁(t) и U₂(t). Функциональная схема корреляционного приемника ЧМ – сигналов на рисунке 6

Рисунок 6

Работа каждого канала аналогична работе рассмотренного выше корреляционного приемника АМ – сигналов. На выходе каждого интегратора в момент окончания каждого интервала анализа с длительностью t_и формируется напряжение, равное Е для «своего» сигнала в составе y(t) и равное 0 для «не своего» ортогонального сигнала в составе y(t). Работа решающего устройства (РУ) и ФЛУ аналогичны рассмотренным выше.

Плотности вероятности значений корреляционных интегралов W₁(Z) и W₂(Z) в одном и другом каналах выглядят так же, как это изображено на рисунке 3. Однако, при этом средняя мощность сигнала на входе приёмника равна мощности элементарных сигналов U₁(t) и U₂(t). Поэтому вероятность ошибочного приема символа может быть вычислена по формуле

Р₀ = Р₀₁ = Р₁₀ = 0,5 [1- Ф(q)].

Вероятность ошибочного приема кодовой комбинации («буквы») при независимых искажениях символов, её составляющих с вероятностью Р_о определяется выражением

где каждое слагаемое определяет числа ошибок в «букве» (от 1 до 5). Более удобное для вычислений вероятности выражение

Р_ош=1-(1-Р_о)⁵,

где второе слагаемое есть вероятность безошибочного приёма 5-символьной «буквы» (кодовой комбинации.

Когерентный прием обеспечивает потенциально достижимые характеристики помехоустойчивости приемников дискретных сигналов.

Реально при неизвестных точно случайных параметрах сигналов применяют некогерентный прием, при котором помехоустойчивость приема снижается по сравнению с потенциальной.

Корреляционный прием требует точного значения моментов прихода элементарных сигналов U₁(t) и U₂(t), чтобы точно подать их копии на перемножители.

Функцию формирования значения корреляционного интервала к моменту окончания интервала анализа может выполнять согласованный линейный фильтр. Он является инвариантным (нечувствительным) к моменту прихода элементарного сигнала и всегда к его окончанию формирует выходное напряжение, совпадающее со значением корреляционного интеграла с точностью до известного постоянного коэффициента. Это обусловлено тем, что импульсная характеристика согласованного фильтра зеркальна по отношению к сигналу, с которым он согласован. Согласованный фильтр заменяет перемножитель коррелятора, интегратор и источник опорной копии сигнала.

В приемниках дискретных радиосигналов моменты окончания анализируемых интервалов для регистрации принятых решений определяются статистически на основании периодичности смены уровней напряжения на выходе решающего устройства за предшествующий значительный интервал наблюдения принимаемого дискретного сигнала.