Ф.7.11-19
С.Е.ТАСАНБАЕВ
ТЕХНОЛОГИИ ЦИФРОВОЙ СВЯЗИ
Шымкент -2011 г.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
РЕСПУБЛИКИ КАЗАХСТАН
южно-казахстанский государственный университет
им. м.ауезова
Кафедра Автоматизации, телекоммуникаций и управления
Тасанбаев С.Е.
ТЕХНОЛОГИИ ЦИФРОВОЙ СВЯЗИ
Лабораторный практикум по дисциплине
для студентов специальности 5В071900 (050719)
«Радиотехника, электроника и телекоммуникации»
Форма обучения: очная, заочная
Шымкент – 2011 г
УДК 621.396
ББК 33.884.1
Составитель к.т.н., доцент Тасанбаев С.Е.
Учебное пособие содержит методические указания к лабораторным работам по дисциплине «Технологии цифровой связи» для студентов специальности 5В071900 (050719) «Радиотехника, электроника и телекоммуникации», Шымкент: ЮКГУ, 2011, 128 с.
Методические указания составлены в соответствии с требованиями учебного плана и программой дисциплины «Технологии цифровой связи» и включает все необходимые сведения по выполнению тем лабораторных работ курса.
Рецензенты: д.т.н., профессор кафедры ПАОС ЮКГУ Бреннер А.М.,
руководитель ППЕНТ № 89 , к.т.н., доцент Каланов C.M.
Рассмотрено и рекомендовано к печати заседанием кафедры АТУ
(протокол № __ от «___» _______ 20___ г.) и методической комиссией факультета ИТТАС (протокол № ___от «__» _____20__ г. )
Рекомендовано к изданию Методическим советом ЮКГУ им. М.Ауезова, протокол № ___ от «____» ______________ 20__ г.
© Южно-Казахстанский Государственный Университет (ЮКГУ), 2011 г.
© Тасанбаев С.Е., 2011 г.
Содержание
Предисловие. Цели и задачи лабораторногопрактикума
Лабораторная работа №1. Исследование статистики ошибок в каналах связи
Лабораторная работа №2. Исследование методов регистрации двоичных сигналов
Лабораторная работа № 3. Изучение краевых искажений в дискретном канале
Лабораторная работа №4. Эффективное кодирование сообщений. Коды Шеннона – Фано, Хаффмена
Лабораторная работа №5. Исследование устройств преобразования сигналов, использующих АМ, ЧМ и ОФМ модуляции
Лабораторная работа № 6. Изучение методов и систем синхронизации
Лабораторная работа № 7. Исследование устройств кодирования и декодирования помехоустойчивых кодов. Коды Хемминга.
Лабораторная работа № 8. Исследование устройств кодирования и декодирования сверточных кодов
Лабораторная работа № 9. Исследование систем передачи информации с обратными связями
Литература………………………………………………………………………
Предисловие. Цели и задачи лабораторного практикума
Целями лабораторного практикума по дисциплине «Технологии цифровой связи» являются формирование у студентов знаний принципов и методов передачи цифровых сигналов, научных основ и современного состояния технологии цифровой связи; получение представления о возможностях и естественных границах реализации цифровых систем передачи и обработки, уяснение определяющих свойств устройств передачи данных и задачи их функционировании.
Задачи лабораторного практикума дисциплины состоят в изучении основных принципов и алгоритмов построения систем цифровой связи, а также в получении практических навыков по методологии инженерных расчетов их основных характеристик и обучении методам технической эксплуатации цифровых систем и сетей. Он углубляет и развивает подготовку инженеров связистов, овладевающих современной технологией построения и передачи цифровой информации.
В результате выполнения лабораторного практикума студенты должны
знать принципы построения систем передачи и обработки цифровых сигналов, аппаратные и программные методы повышения помехоустойчивости и скорости передачи цифровых систем связи, методы повышения эффективного использования каналов связи;
уметь производить расчеты основных функциональных узлов, осуществлять анализ влияния внешних факторов па работоспособность средств связи;
иметь навыки применения средств компьютерной техники для расчетов и проектирования программно-аппаратных средств связи.
Лабораторный практикум выполняется в среде приложений МАТЛАБ, LabVIEW, VisSim, а также с использованием разработанных приложений.
Лабораторная работа 1 Исследование статистики ошибок в каналах связи
Цель работы: исследование статистики ошибок в цифровом канале связи с пакетированными ошибками.
1. Краткие теоретические сведения.
1.1. Использование имитационной модели цифрового канала передачи данных значительно упрощает задачу проектирования систем связи, так как предварительное проведение необходимых модельных экспериментов позволяет ответить на вопросы о корректирующих способностях исследуемых кодеков, и осуществить рациональный подбор параметров к конкретному цифровому каналу.
К имитационной модели канала предъявляется ряд разумных требований. Во-первых, модель должна адекватно отражать статистику ошибок в имитируемом ею канале, во-вторых, модель должна предоставлять возможность исследователю оценить ряд основных параметров, рекомендованных Международным институтом электросвязи ITU-T к измерению в бинарном канале (рекомендации G.821, G.826 и M.2100). В-третьих, необходимо иметь возможность оценивать различные аспекты применения помехоустойчивых кодов для последующей реализации в цифровых каналах, например: требования к объему буферной памяти, учет быстродействия кодера и декодера, требования к качеству цифровых каналов, степень устойчивости к изменениям характеристик канала. В-четвертых, модель должна быть удобной в использовании, то есть должна быть предоставлена возможность легко управлять характеристиками канала, хранить параметры и результаты проведенных экспериментов и так далее. [9]
1.2 Модель источника ошибок
В данном разделе рассмотрим важнейшую составляющую часть имитационной модели – модель источника ошибок. Очевидно, что от корректности её построения зависит выполнение основного требования к модели канала – отображение ею основных свойств моделируемых реальных каналов.
К сожалению, в программном продукте MatLab отсутствует модель канала с пакетированными ошибками, поэтому такая модель была самостоятельно создана на основе, и с учетом требований для последующего использования в Simulink.
Определяющим моментом в создании имитационной модели источника ошибок является предварительное построение ее математической модели.
1.1.1 Математическая модель
Простейшей моделью, основанной на применении математического аппарата марковских цепей является модель источника ошибок, предложенная Д. Гильбертом.
Согласно этой модели канал может находиться в двух состояниях – «хорошем» (состояние 1) и «плохом» (состояние 2). «Хорошее» состояние характеризуется отсутствием ошибок. В «плохом» состоянии ошибки возникают с вероятностью E.
Если при передаче элемента аi канал находится в «хорошем» состоянии, то при передаче следующего элемента аi+1 канал будет находиться в том же состоянии с вероятностью Р и в «плохом» состоянии - с вероятностью 1-Р. Если же при передаче элемента аi канал находился в «плохом» состоянии, то при передаче элемента аi+1 он может находится в том же состоянии с вероятностью Q и в «хорошем» состоянии - с вероятностью 1-Q.
(1.1)
Рис. 1.1 Матрица переходов из состояния в состояние
Если P и Q достаточно велики, но не равны между собой, то наблюдается тенденция к сохранению возникшего состояния 1 или 2, что имитирует канал с пакетами ошибок.
Средняя вероятность нахождения канала в хорошем состоянии:
(1.2)
Среднее число элементов в хорошем состоянии:
(1.3)
Средняя вероятность нахождения канала в плохом состоянии:
(1.4)
Среднее число элементов в плохом состоянии:
(1.5)
Средняя вероятность возникновения ошибки:
(1.6)
Рассмотренная модель описывается тремя параметрами: P, Q, E, которые в реальных каналах могут быть найдены экспериментально.
1.1.2 Алгоритм работы
В соответствии с математической моделью был построен алгоритм работы источника пакетированных ошибок, приведенный на рис.1.2. Генерируется битовый поток, в котором, отсутствие ошибки обозначается – «0», а наличие ошибки – «1».
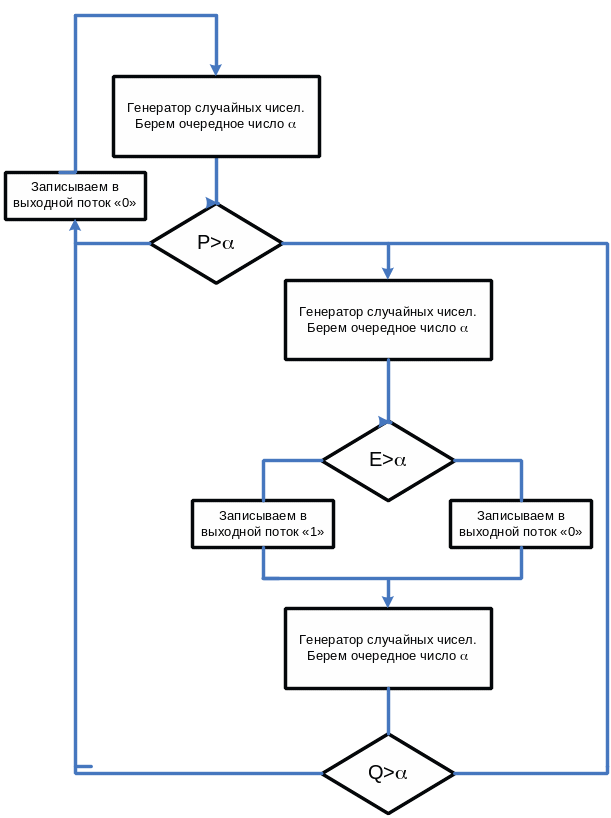
Рис. 1 Алгоритм работы источника пакетированных ошибок
1.1.2 Программная реализация
Программная реализация модели была выполнена в САПР Simulink из пакета MatLab. Модель Simulink – это графическая блок-диаграмма изображенная на рис.2.
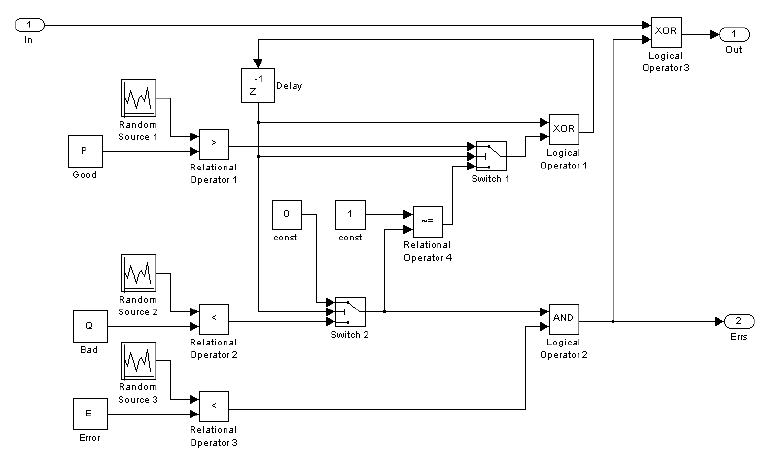
Рис.2 Модель канала с пакетированными ошибками
На вход модели «In» подается информационная последовательность передаваемых данных. Модель генерирует поток ошибок в соответствии с алгоритмом, указанным на рис.1. Модель изменяет данные, полученные на вход модели «In» и передает их на выход «Out». Так же существует возможность передачи потока ошибок отдельно на выход «Errs».
В дальнейшем изложении, будем изображать модель в виде одного блока «Hilbert Channel Model» (названного в честь Д. Гилберта) изображенного на рис.3 и управляемого при помощи параметров: P, Q, E. (см. рис.5)
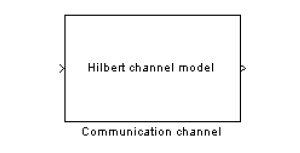
Рис.3 Блок «Hilbert Channel Model»
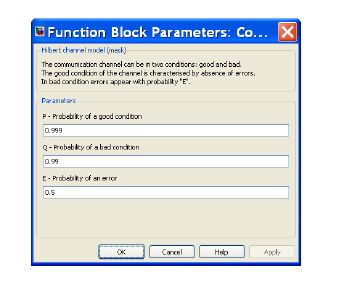
Рис.5 Параметры блока «Hilbert Channel Model»
В Приложении 1 приведен фрагмент экспериментальной записи потока пакетированных ошибок при использовании следующих параметров: P=0.999, Q=0.99, E=0.5 (средняя Perr=0.0455). В Приложении 2 приведен фрагмент экспериментальной записи потока независимых ошибок, сгенерированных блоком «Binary Symmetric Channel» при использовании параметра: Perr=0.0455. Несложно заметить, как сильно различается распределение ошибок в этих потоках, несмотря на то, что средняя вероятность появления ошибки одинакова.
ПРИЛОЖЕНИЕ 1 Фрагмент экспериментальной записи потока пакетированных ошибок при использовании следующих параметров: P=0.999, Q=0.99, E=0.5 (средняя Perr=0.0455). …..10011010111001111111001101111000111011001000101100100101110011000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000010010011000000100111100001011101101001011111101000100101011101110111010111000111011011010001111000011101110111001111111111111010001101011010011100111001111100110101100011100001010010001011011111101000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000001100110101110101001000000011000010111001101110000000000000000000000000000000000000000000000000000000000000000000000000000000000…..
ПРИЛОЖЕНИЕ 2 Фрагмент экспериментальной записи потока независимых ошибок сгенерированных блоком «Binary Symmetric Channel» при использовании параметра: Perr=0.0455. …..000000000000000000000000000000000000100100000000001000000000000001000000000000000000100000000000000000000010000000001000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000100110010000000000000000001000000001010000000000000000000000000000000000001000000000000000000000000000010000000000000000000010000000000000000000000000000010000000000000000100100000000000000000000000000010000000000000000000000100000000000000000001000000000000000000000000000000000000000000100000000000000000000000000000000000000000000000000000000000000000000001000000000100000000000000000000000000000000000000000000000000110000000000000000000000000000000000000000000000000000000000000000000000000000100000000000000001000000000000000010000000000000000000000000000000000010000000000000000000000000000000000010000000000100000000000000000000010000000000000000000000000000000000000000000100000000000000000000000000000000000000000000000000000000000100000000000000000000000000000000000000000000000000000000000000000000000000100000000010000000000000000001000000000000011000000100001000000000000000000000000000000000000000010000000000000000000010000000000000010000000000000000010000000000000000000101000000000000000000000000000001000000100000000000000000000000000000010000000000000000000000000000000000000000000000000000000001000000000000001000000000001000000000000000010000000100000110000000000010000000100000000000000000000000000000000000000000000000000000000000000010000000000000000000000000000000000000000000000000000000000000000000000000000000100000100000000000000000010000000000000000000000000000000000000000000000100000000000000101000000000000000000000000001001000000000000000000000000100000000000000000000100100001000000100000000000000000000000000000010000000000000000000000000000001000000000000000010000000000000000000000000000100000000000000100000000000000000000000000000000000000000000000000000000000100000000000000000000000000000000000000001000000000000000000000100000000010000000000000000000000000000000000000000010000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000100000000000000000000000000000000000000000100000000000000000000000000000000000000000000000000000000000010000000000000000000001000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000001000100000000100001100101000000100000001000010000000010000000000110000000000…..
ПРИЛОЖЕНИЕ 3 Источник пакетированных ошибок. Реализации при помощи функции bursterrorsstream (P, Q, E, N)
% Функция генерации потока пакетированных ошибок
function [A] = bursterrorsstream (P, Q, E, N)
% A - Возвращаемый одномерный массив, где "1" - ошибка
% P - Вероятность нахождения канала в "хорошем" состоянии
% Q - Вероятность нахождения канала в "плохом" состоянии
% E - Вероятность возникновения ошибки
% N - Минимальный требуемый размер возвращаемого массива
format long
A = zeros();
n = 0;
% Пока возвращаемый массив не достиг требуемого размера
while n < N
n = n + 1;
b = rand(1);
% Пока канал находится в "хорошем" состоянии
while b < P
% Записываем в массив "0"
A(n) = 0;
n = n + 1;
b = rand(1);
end
% Когда канал перешел в "плохое" состояние
% И если возникла ошибка
b = rand(1);
if b < E
% Записываем в массив "1"
A(n) = 1;
end
b = rand(1);
% Пока канал находится в "плохом" состоянии
while b < Q
n = n + 1;
b = rand(1);
% И если возникла ошибка
if b < E
% Записываем в массив "1"
A(n) = 1;
end
b = rand(1);
end
% Когда канал перешел в "хорошее" состояние
% Записываем в массив "0"
n = n + 1;
A(n) = 0;
end
end