6. План практических занятий
Код занятия |
Тема |
ПЗ 1 |
Множество. Подмножество. Способы задания множеств. Отношения между множествами. Операции над множествами |
ПЗ 2 |
Прямое произведение множеств. Бинарные отношения. Способы задания бинарных отношений. Их свойства и виды. Отображения. Виды отображений |
ПЗ 3 |
Основные комбинаторные конфигурации: сочетания, размещения, перестановки (без повторений и с повторениями). Основные правила комбинаторики: правило суммы и правило произведения. Бином Ньютона |
ПЗ 4 |
Элементарные булевы функции. Суперпозиция. Способы задания булевых функций. Свойства элементарных булевых функций. Двойственная булева функция |
ПЗ 5 |
Аналитические способы задания булевых функций: ДНФ, КНФ, СДНФ, СКНФ, полином по модулю два |
ПЗ 6 |
Реализация булевых функций контактными схемами и схемами из функциональных элементов. Упрощение контактных схем |
ПЗ 7 |
Функционально замкнутые классы булевых функций. Полные системы булевых функций Функционально замкнутые классы булевых функций. Полные системы булевых функций |
ПЗ 8 |
Корректирующие коды. Коды Хэмминга. Корректирующие коды максимальной мощности |
ПЗ 9 |
Некоторые свойства кодов. Эффективное кодирование. Коды Фано, Шеннона, Хаффмена |
ПЗ 10 |
Основные понятия теории графов. Виды графов. Способы задания графов. Планарные графы. Группы автоморфизмов графов |
ПЗ 11 |
Задачи на графах: задача о независимом множестве вершин, задача о клике, задача о покрывающем множестве вершин |
ПЗ 12 |
Задачи на графах: задача о доминирующем множестве вершин, задача о вершинной раскраске, задача коммивояжера |
ПЗ 13 |
Задача о последовательных станках. Задача о 2-х последовательных станках. Задача о параллельных (идентичных) станках |
ПЗ 14 |
Периодические однопроцессорные расписания (в дискретном времени). Задача сетевого планирования |
ПЗ 15 |
Формализация понятия «алгоритм». Машина Тьюринга |
7. Материалы для срс
СРС. Семестровое задание Элементы теории множеств
Задание № 1
Доказать тождество, используя определение равных множеств.
А\В=А\(АВ)
А\В=(АВ)\В
А(В\С)=(АВ)\(АС)
(АВ)\С)=(А\С)(В\С)
(А\С)(В\С)=(АВ)\С
(А\В)\С=А\(ВС)
А\(В\С)= (А\В)(АС)
(А\В)(С\D)= (АС)\(ВD)
A(B∆C)=(AB)∆(AC)
A∆B=(AB)\(AB)
(A∆B)(AB)=AB
(A\B)B=AB
(A\B)(AB)=A
A\(A∆B)=AB
AB=(A
)(
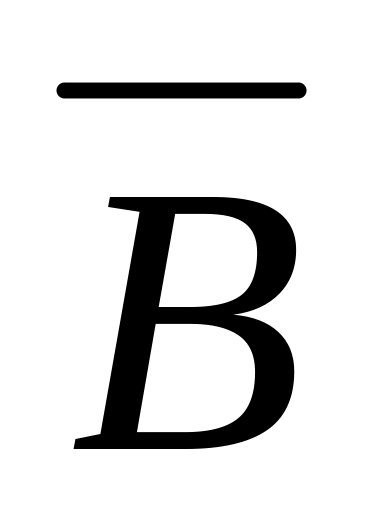B)(AB)C=(AC)(BC)
A(BC)=(AB)(AC)
AB=A( B)
(AB)\(AB)=(A\B)(B\A)
A\(BC)=(A\B)(A\C)
Задание № 2
Даны множества А, В и С. Составить прямые произведения множеств А´В´С и В´С´А.
A={1,3}; B={1,2,5}; C={2,4}
A={2,5}; B={3,4,5}; C={1,3}
A={2,1,3}; B={1,5}; C={4,6,7}
A={1,3,5}; B={1,2}; C={4,6}
A={2,3}; B={3,6}; C={4,7}
A={1,2,3}; B={4,5}; C={6,7,8}
A={1,2}; B={2,3,5}; C={7,9}
A={1,3,4}; B={2,4,5}; C={8,9}
A={1,2,7}; B={5,9}; C={1,2,3}
A={1,2,7}; B={2,3}; C={3,5}
A={1,2,3}; B={3,4}; C={4,5,7}
A={7,3}; B={3,1}; C={4,5}
A={3,2,1}; B={7,2}; C={5,8,7}
A={2,8}; B={3,7,4}; C={2,3}
A={7,3,5}; B={2,4,8}; C={1,9}
A={4,8}; B={9,1}; C={7,5}
A={9,8}; B={3,1,4}; C={2,9}
A={0,2,8}; B={6,10}; C={1,2,4}
A={7,2,6}; B={2,5}; C={3,4}
A={2,6}; B={9,7,4}; C={3,5}
Задание № 3
Найдите область определения и область
значения бинарного соответствия,
A´B,
если:
r={(x,y)| 2x-y=7}, A={-8;-7;-1;0;2;4},B={-21;-5;0;1;3}
r={(x,y)| (x+y)M5},A={-8;-7;-1;0;2;4;5;7}, B={-25;-23;-9;-7;-6;0;1;3}
r={(x,y)| 2x-5y<-7}, A={ -2;-1;1;3;2}, B={-5;-2;2;5;3;4}
r={(x,y)| (x-y)M4}, A={ -2;-1;1;3;2},B={-5;-2;2;5;3;4}
r={(x,y)| 2x+5y>-10}, A={-20;-15;-10;0;1;4;7}, B={-3;-2;0;2;5;7}
r={(x,y)| -2x-y=5}, A={-2;1;0;5;-1;2;4}, B={-9;-8;-5;-1;-4;0}
r={(x,y)| (2x+y)M3},A={-2;-1;0;5;-1;2;4},B={-9;-8;-5;-1;-4;0}
r={(x,y)|4x-3y>-8}, A={-5;-4;5;3;-2}, B={0;3;32;5;6;1}
r={(x,y)|(x+y)M3}, A={-5;-4;5;3;-2},B={0;3;32;5;6;1}
r={(x,y)| 3x-y>8}, A={-4;-3;-2;4;-1;2}, B={-3;3;-10;4;2}
r={(x,y)| (x-y)M5},A={-4;-3;-2;4;-1;2},B={-3;3;-10;4;2}
r={(x,y)| (x-y)M3}, A={0;1;2;3},B={1;2;3;4;8}
r={(x,y)| 2x>y},A={0;1;2;3},B={1;2;3;4;8}
r={(x,y)| 2x-5y<-7},A={-4;-2;0;3;2;7;-1}, B={-3;-5;1;2}
r={(x,y)|(x+2y)M5},A={-20;-15;-7;-4;1;2;0},B={-4;-2;0;3;2}
r={(x,y)|(4x-3y)>-8}, A={-5;-4;5;2;3}, B={0;3;5;32;1}
r={(x,y)|(x+2y)M3}, A={-5;-4;5;2;3}, B={0;3;5;32;1}
r={(x,y)| 7x-5y=2},A={-5;-4;0;1;4}, B={-10;-6;0;1;2;8}
r={(x,y)| (x-y)M5}, A={-5;-4;0;1;4}, B={-10;-6;0;1;2;8}
r={(x,y)|3x-2y=-15},A={-6;-5;-2;0;1;2},B={-10;-9;0;1;7;5}
Задание № 4
Выяснить, является ли бинарное соответствие ÎA´B отображением; если да, то определить инъективно, сюрьективно или биективно это отображение.
xryÛ(x+y)M2 , A=B={-1;0;1;2;3}
xryÛy=sin x , A={-p/2;0;p/2;p/3;p},
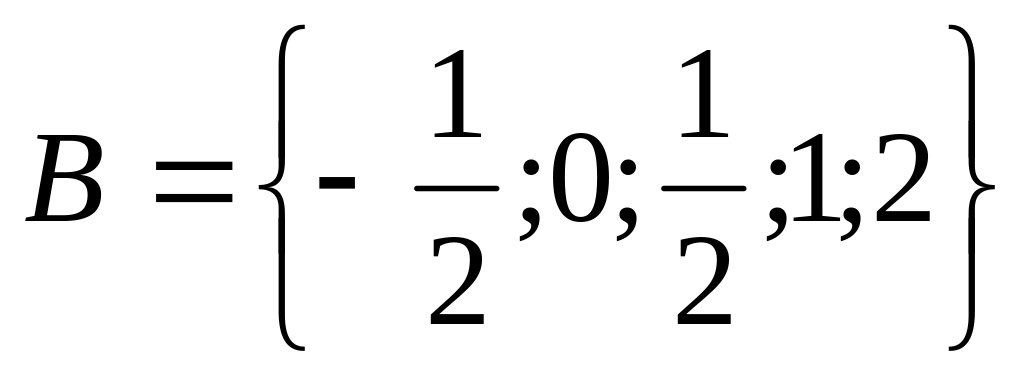
r={(m;2),(n;3),(p;5),(q;2)}, A={m;n;p;q}, B={2;3;5}
r={(a1;b3),(a2;b1),(a3;b1)}, A={a1,a2,a3}, B={b1,b2,b3}
r={(a;0),(b;0),(c;1),(b;1)}, A={a;b;c;d}, B={0;1}
r={(a;2),(b;0),(c;1)}, A={a,b,c}, B={0,1,2}
r={(a;0),(b;1),(c;1),(d;1)}, A={a,b,c,d}, B={0,1}
r={(x,y)| |x|=y}, A=B=R
r={(x,y)| x=|y|}, A=B=R
xryÛ x=lg y , A=B=R
Пусть А={0,1} найти все отображения множества А в себя, указать вид каждого.
Найти все отображения А={a,b,c} на множество В={1,2}
xryÛ(x-y)M2 , A=B={-1;0;1;2;3}
xryÛy=cosx, A={-p/2;0;p/2;p/6;p},
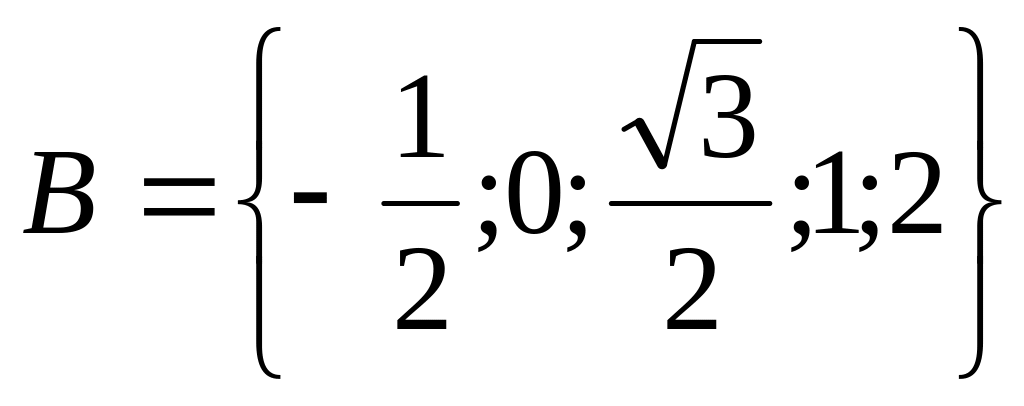
r={x,y}| |x|=y}, A=B=Z
r={(a;0),(b;0),(c;0),(a;1)}, A={a,b,c}, B{0,1}
xryÛ(x+2y)M2}, A=B={-1;0;1;2;3}
Комбинаторика
Задание № 5
Сколькими способами можно раскрасить диаграмму из пяти столбцов пятицветной шариковой ручкой так, чтобы каждый столбец был окрашен в определённый цвет?
Сколько словарей надо издать, чтобы можно было непосредственно выполнять переводы с любого из пяти языков: русского, немецкого, английского, французского, итальянского – на любой другой из этих пяти языков?
Имеется 7 кружков: 5 белых и 2 чёрных. Сколько различных узоров можно составить из этих кружков, располагая их в ряд?
В стену здания вмонтированы 10 гнёзд для флажков. В каждое гнездо вставляется либо синий, либо красный флажок. Сколько различных случаев распределения флажков на здании?
В магазине продаются открытки 12 видов. Сколькими способами можно купить 14 открыток?
Научное общество состоит из 20 человек. Надо выбрать президента общества, вице-президента, казначея. Сколькими способами могут быть сделаны эти выборы, если каждый член общества может занимать лишь один пост?
Сколько шестизначных чисел можно составить из цифр 1, 2, 3, 4, 5, 6 дез повторений?
При наборе телефонного номера абонент забыл 2 последние цифры. Сколько пар цифр ему придётся перебрать, если он помнил, что эти цифры чётные и разные?
Сколько различных музыкальных фраз можно составить из 6 нот, допуская повторение одних и тех же звуков? (клавиатура пианино содержит 88 клавиш)
Сколькими способами можно составить список из 15 человек?
Имеется 5 одноцветных пешек и 2 одноцветных коня. Сколькими способами можно их расставить в ряд?
Сколько различных музыкальных фраз можно составить из 6 нот, не допуская повторение одних и тех же звуков? (клавиатура пианино содержит 88 клавиш)
В группе 27 студентов. Из них надо выбрать старосту и зам. старосты. Сколькими способами могут быть сделаны эти выборы, если каждый студент может занимать лишь одну должность?
Сколько можно составить четырёхзначных чисел из 5 разных цифр: 1, 2, 3, 4, 5?
Сколько можно составить чётных четырёхзначных чисел из 4-х разных цифр 2, 3, 5, 7 без повторений?
Для дежурства в группе в течение недели (кроме воскресенья) выделены 6 студентов. Сколькими способами можно установить очерёдность дежурств, если каждый студент дежурит один раз?
Для проведения экзамена создаётся комиссия из 2-х преподавателей. Сколько различных комиссий можно составить из 5 преподавателей?
На втором курсе в первом семестре изучается 10 различных дисциплин. Сколькими способами можно составить расписание занятий на субботу, если в этот день должно быть 3 различные пары?
Сколько шестизначных чисел, кратных 5, можно составить из цифр 1, 2, 3, 4, 5, 6 при условии, что в числе цифры не повторяются?
Сколько различных перестановок можно образовать из букв слова «задача»?
Задание № 6
Найти , если
Найти , если
Найти , если
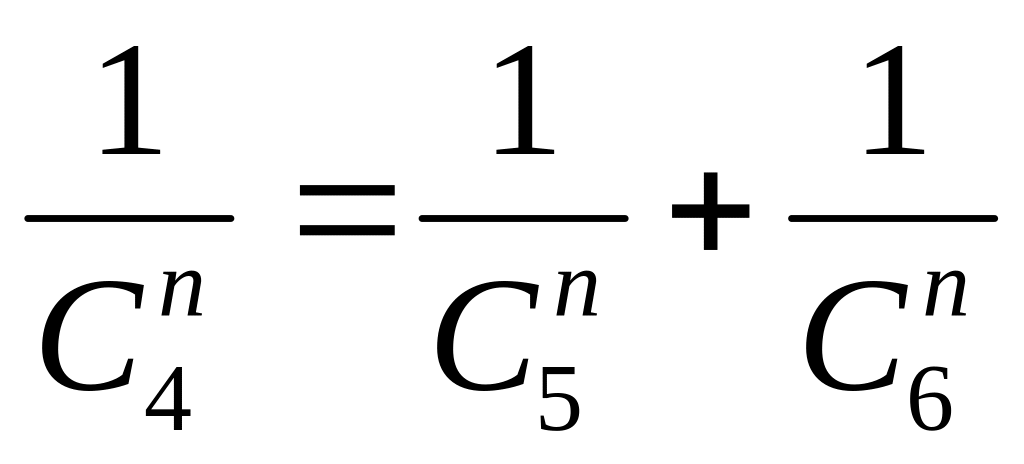
Найти , если
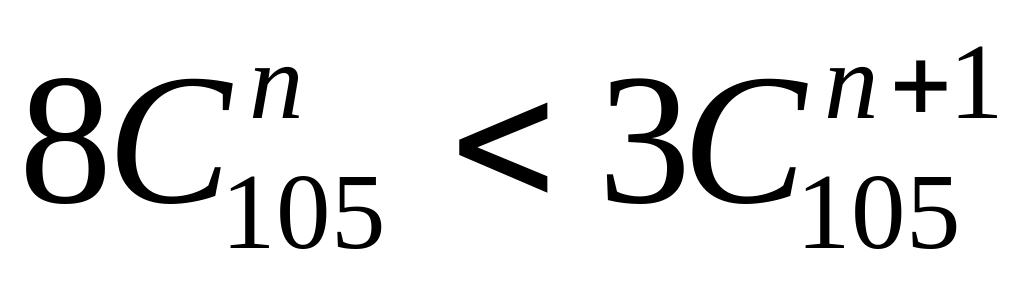
Найти , если
Найти , если
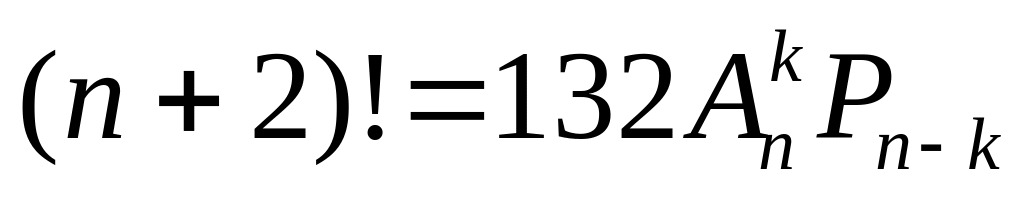
Найти , если
Найти , если
Найти , если
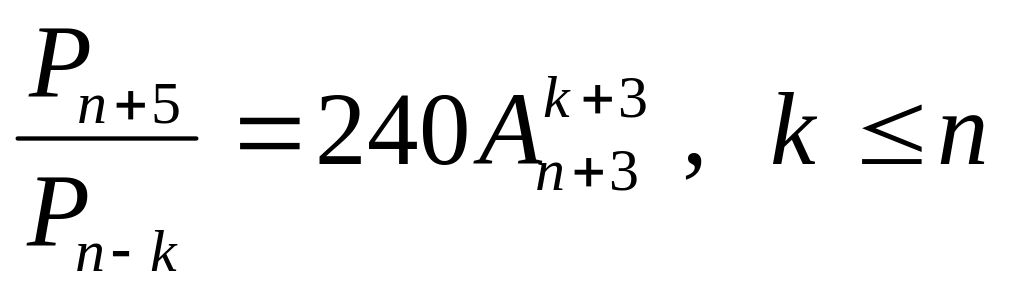
Найти , если
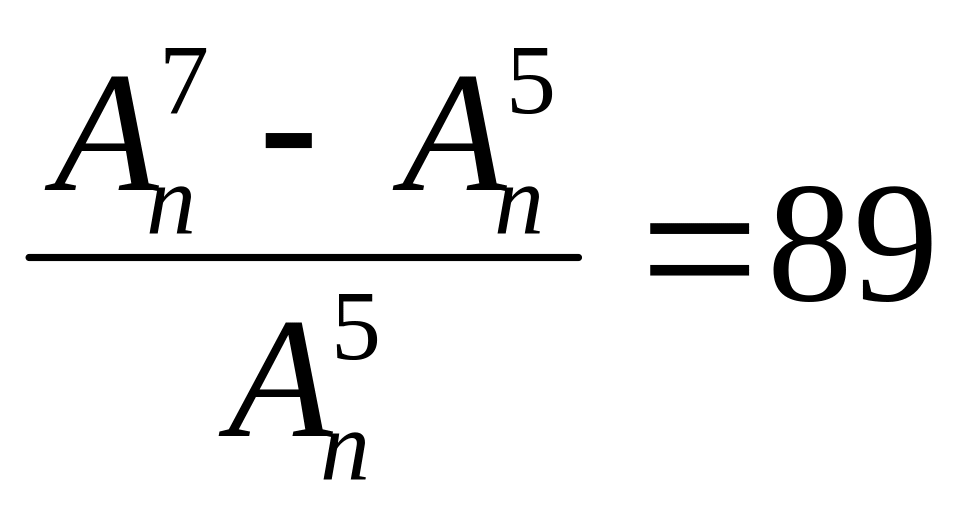
Найти , если
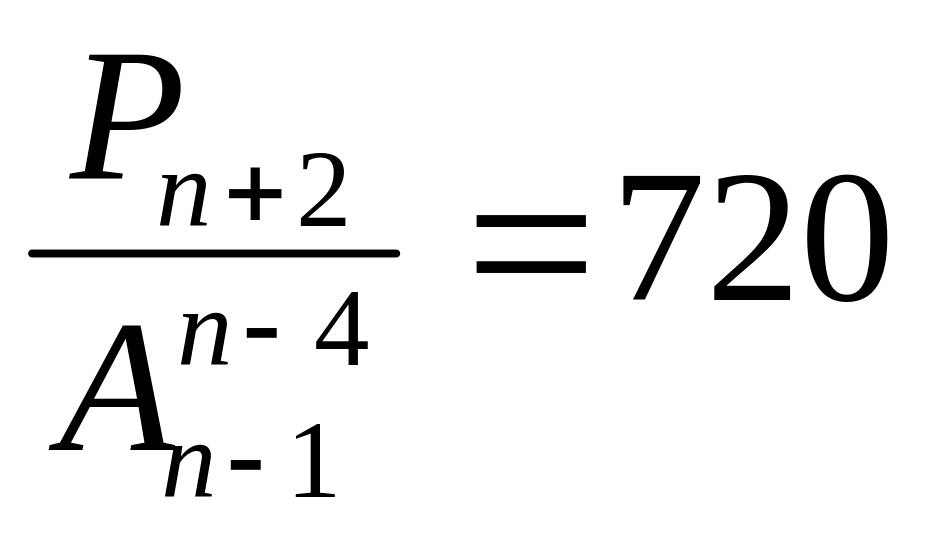
Найти , если
Найти , если
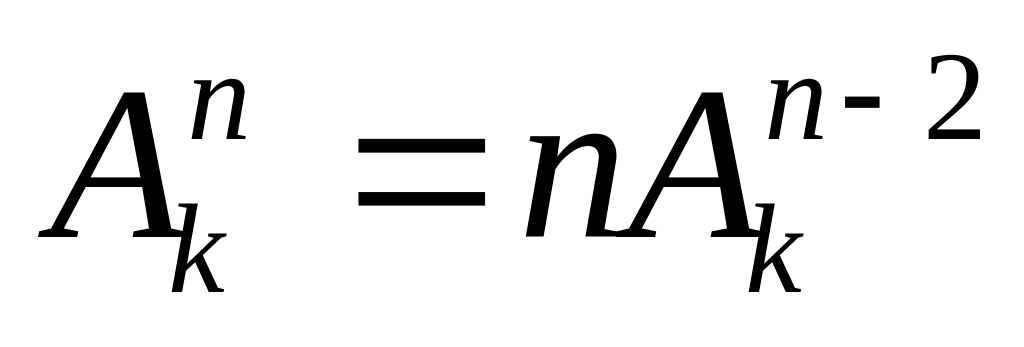
Найти , если
Найти , если
Найти , если
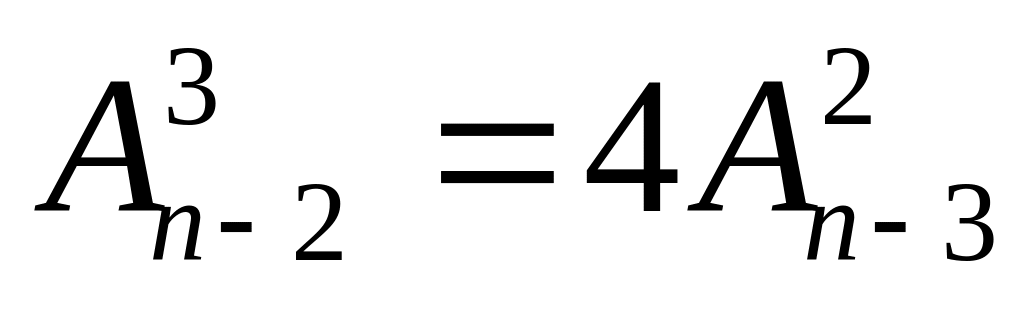
Найти , если
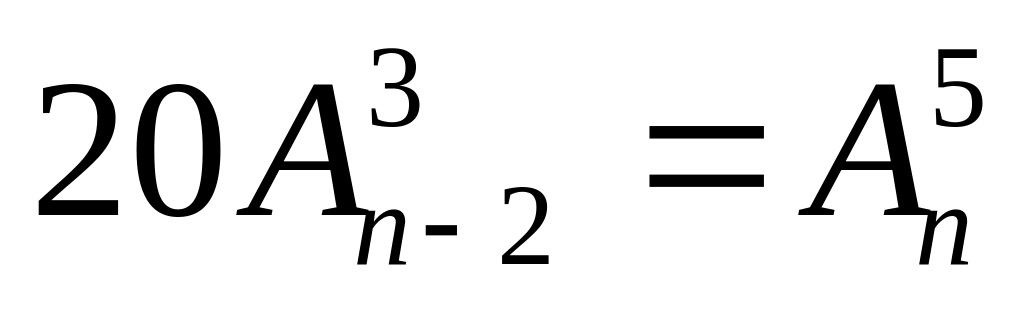
Найти , если
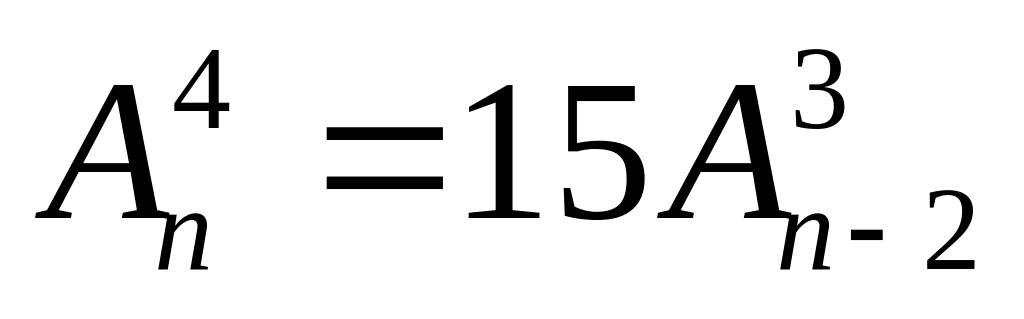
Найти , если
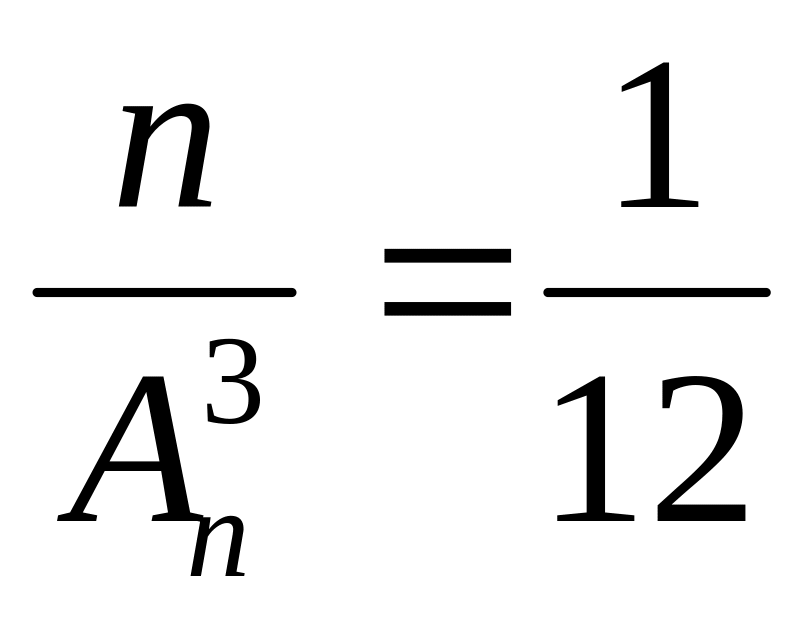
Найти , если
Задача № 7
Найти четвёртый член разложения бинома
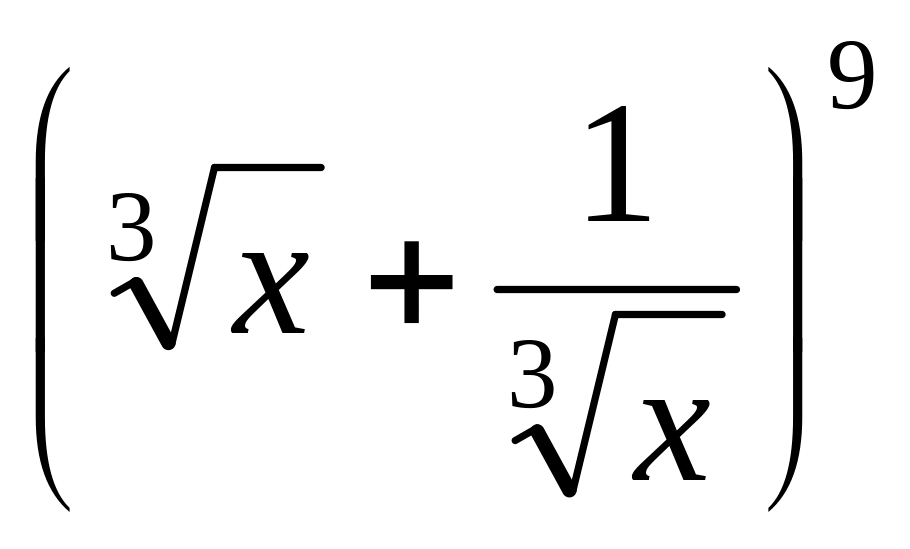
Найти член разложения бинома
,
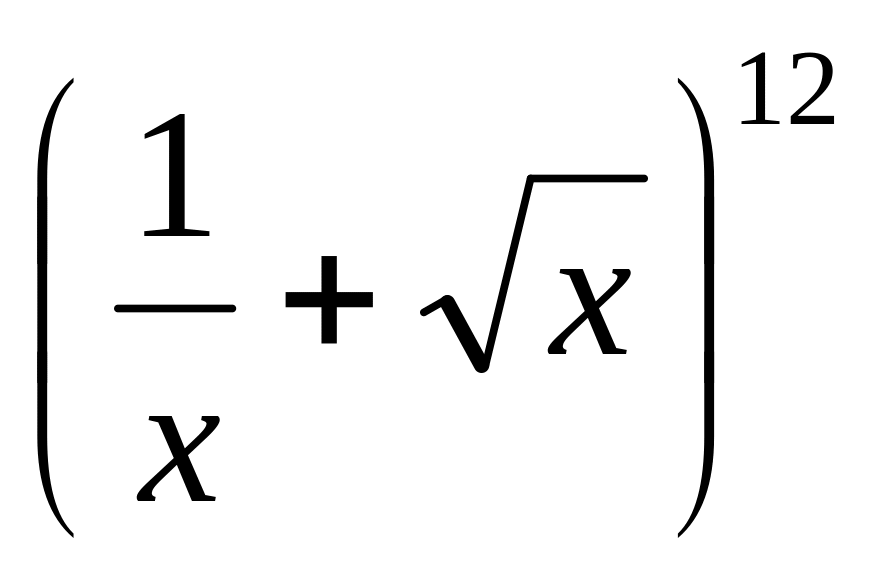не зависящий от
.Найти наибольший коэффициент многочлена
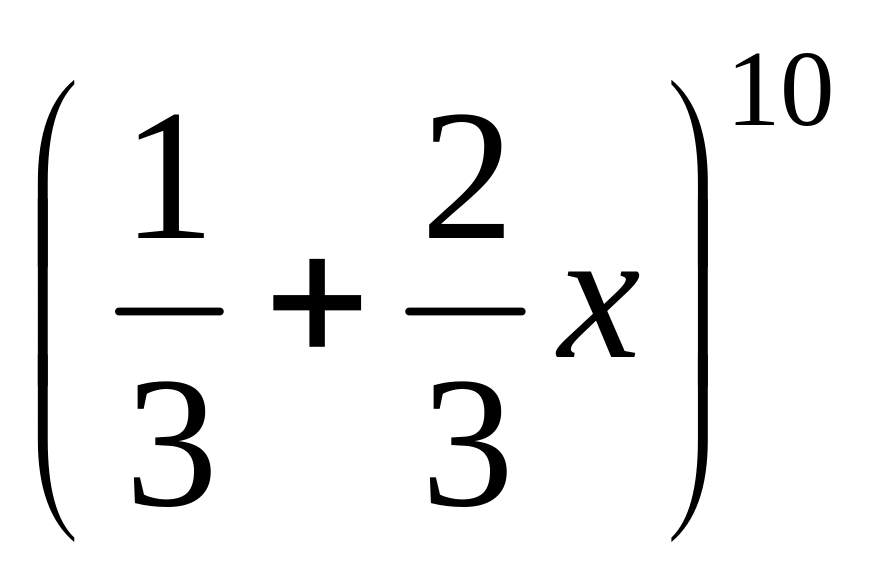.Найти средний член разлолжения бинома
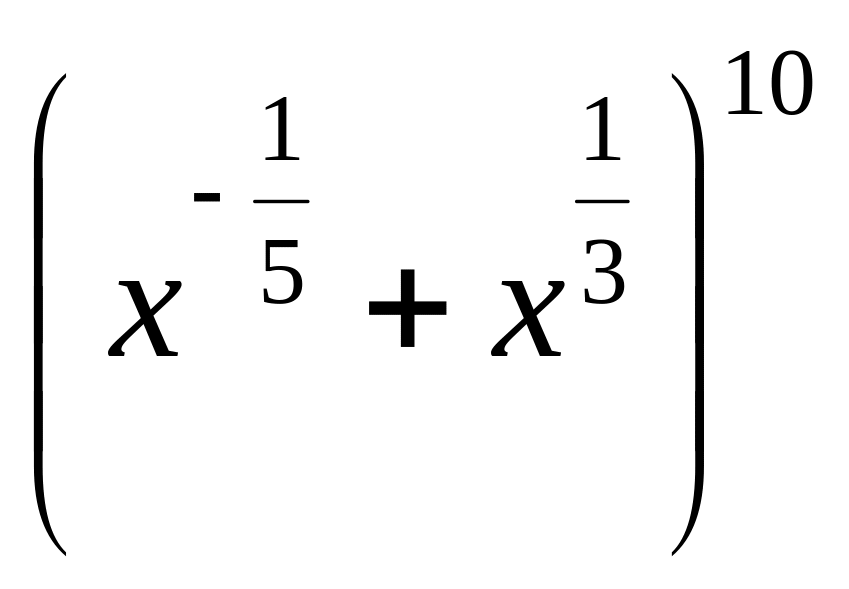
Найти члены разложения бинома
,
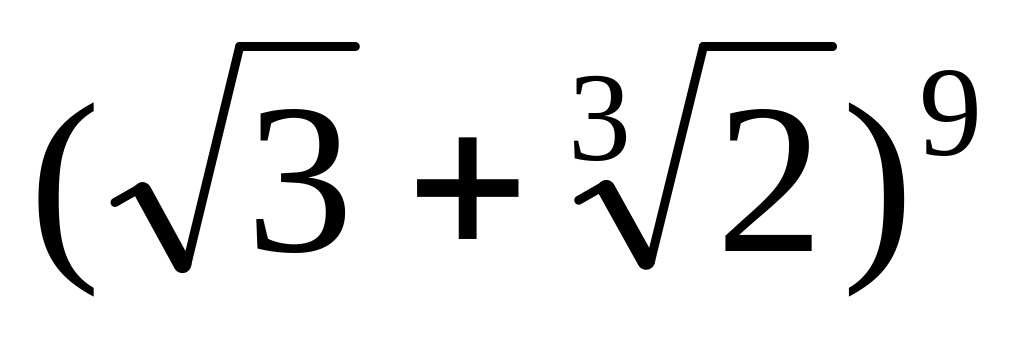являющиеся целыми числами?Найти коэффициент многочлена
при
.Найти седьмой член разложения бинома
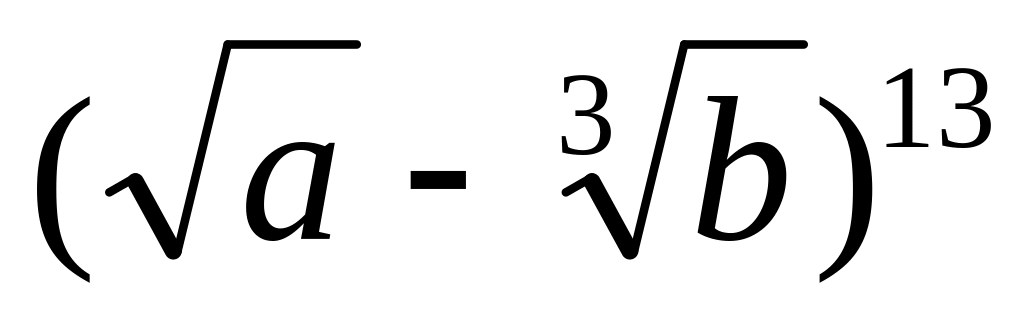.Найти члены разложения бинома
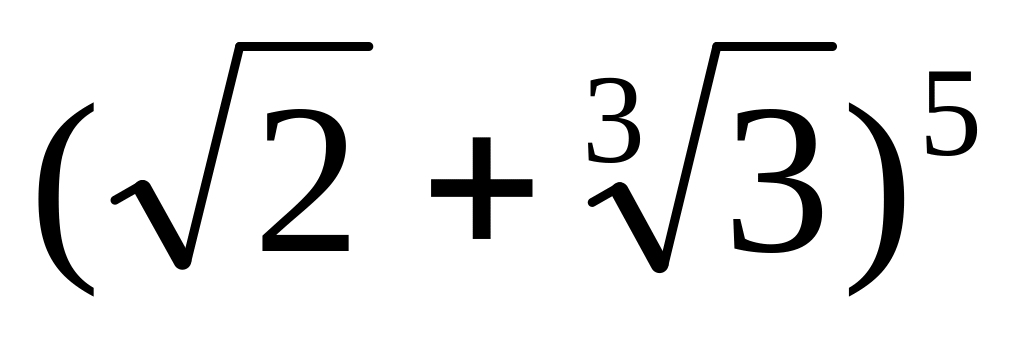
Найти коэффициент многочлена
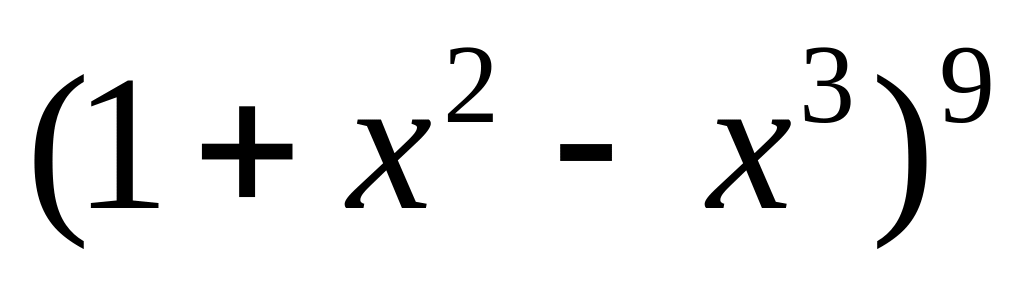при
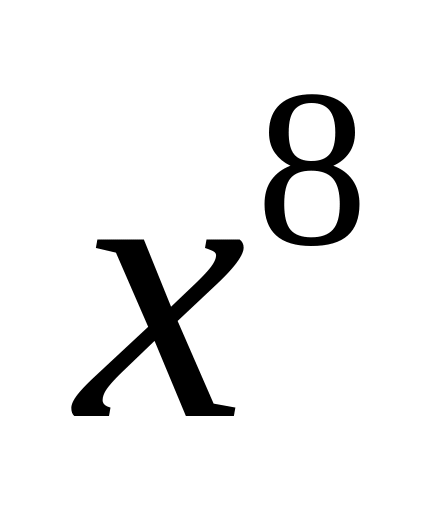.Найти член разложения бинома
,
не зависящий от
.Найти член разложения бинома
,
содержащий
.Найти член разложения бинома
,
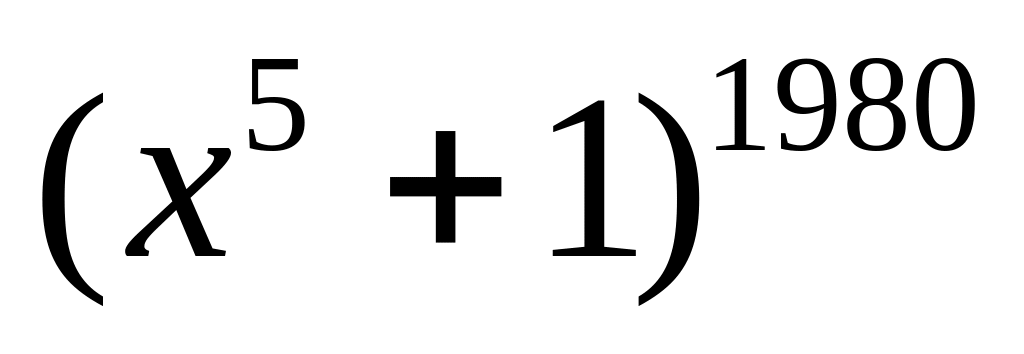содержащий
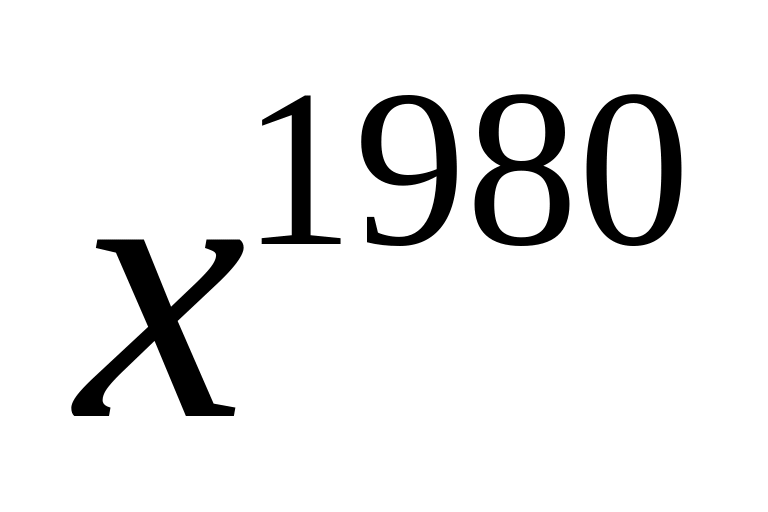.Найти члены разложения бинома
,
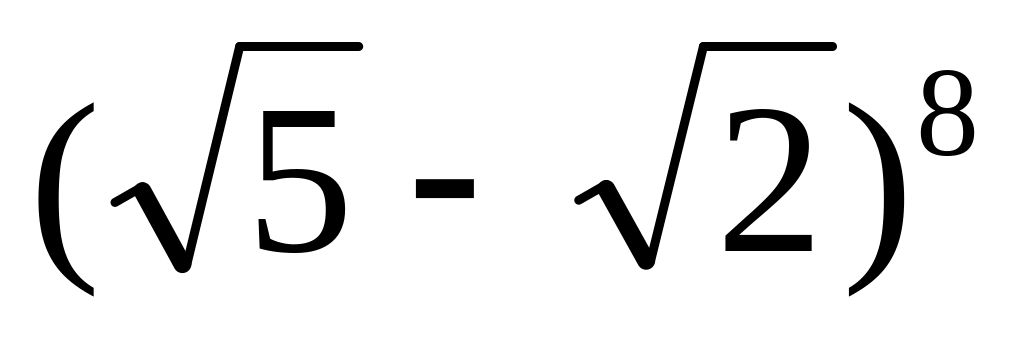являющиеся целыми числами.Найти коэффициент многочлена
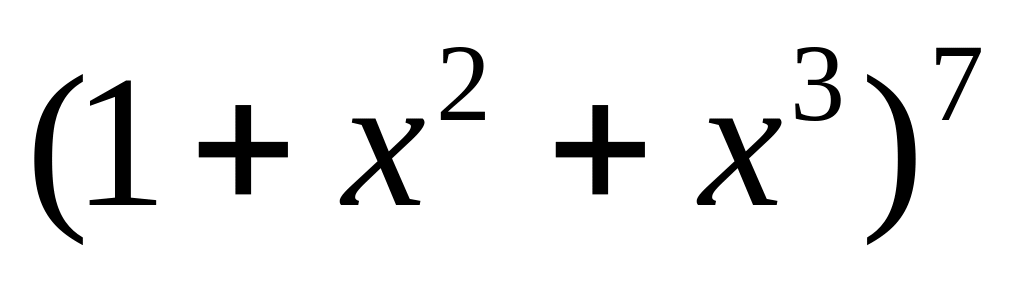при
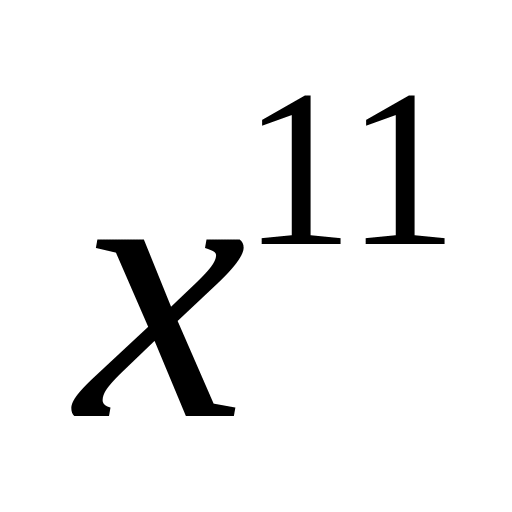.Найти пятый член разложения бинома
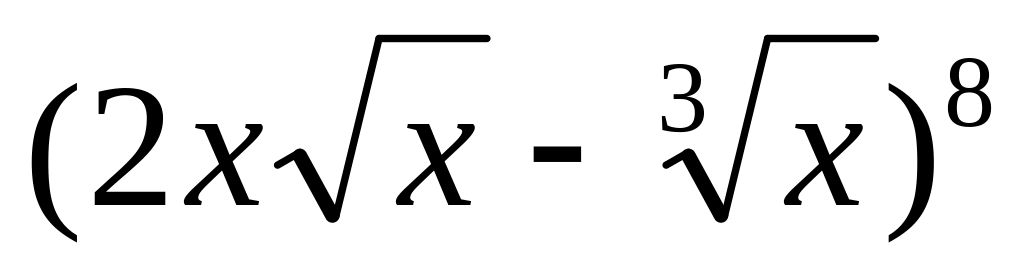.Найти средний член разложения бинома
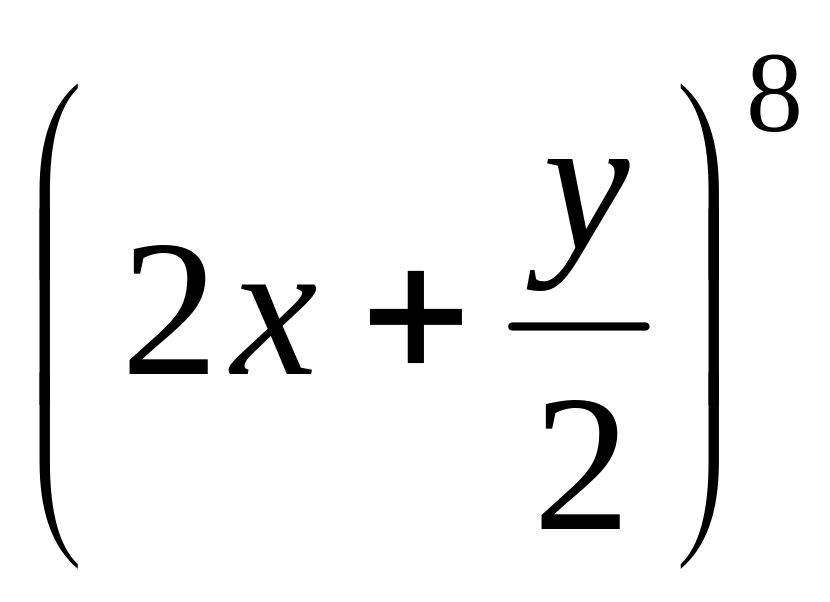.Найти член, содержащий в разложении бинома
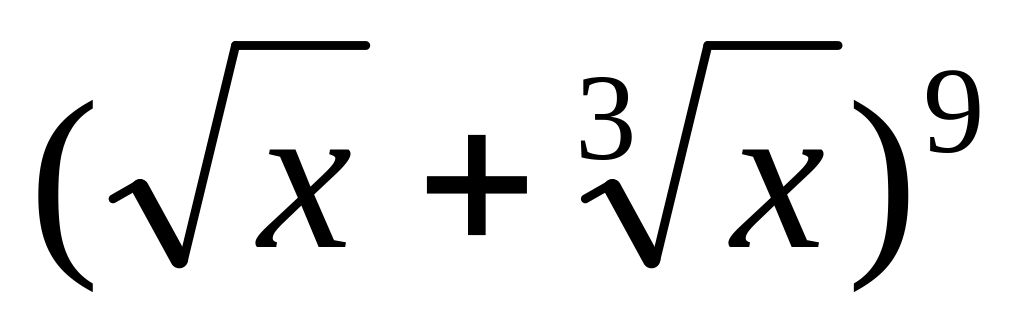.В разложении бинома
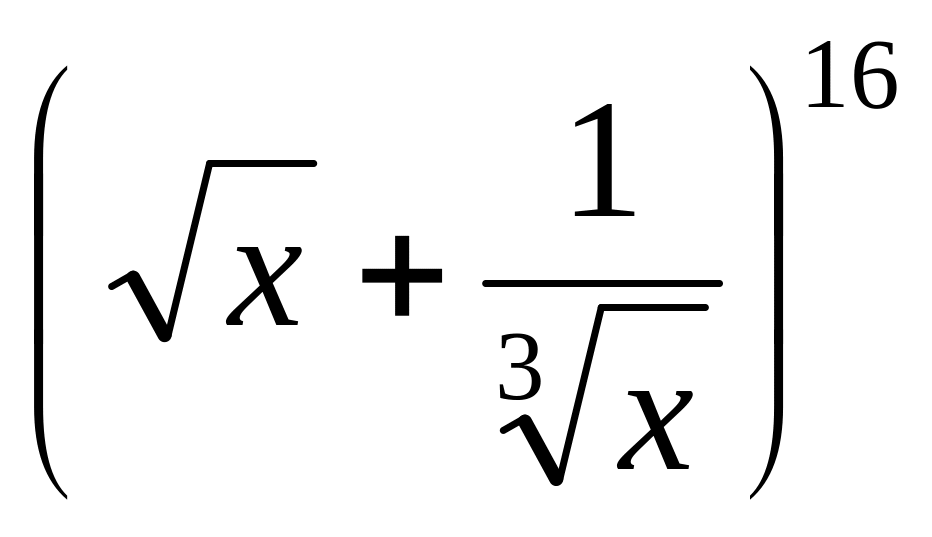найти член, содержащий
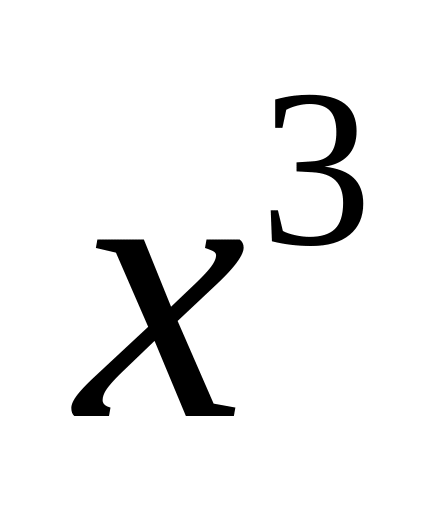.В разложении бинома
найти член, не зависящий от
.Найти четвёртый член разложения бинома
Булевы функции
Задание №8
Булева функция
задана своим вектором значений.
Найти СДНФ, СКНФ функции .
Представить в виде полинома по модулю 2 (метод неопределённых коэффициентов, на основе СДНФ, на основе СКНФ).
Сократить СКНФ, СДНФ.
Построить контактные схемы для СДНФ, СКНФ, а также для сокращённых формул.
№ варианта |
|
1 |
(10101000) |
2 |
(00110101) |
3 |
(01011001) |
4 |
(11001010) |
5 |
(10100110) |
6 |
(00110010) |
7 |
(01010000) |
8 |
(10001101) |
9 |
(10110100) |
10 |
(11010000) |
11 |
(01001010) |
12 |
(01100100) |
13 |
(01110010) |
14 |
(10010100) |
15 |
(00010101) |
16 |
(10101010) |
17 |
(01010011) |
18 |
(10010011) |
19 |
(11100101) |
20 |
(01101100) |
Задание № 9
Решить булево уравнение:
1)
2)
3)
4)
5)
6)
7)
8)
9)
10)
11)
12)
13)
14)
15)
16)
17)
18)
19)
20)
Теория кодирования
Задание № 10
Для заданной длины кодовых слов построить код Хэмминга. Выяснить, является ли этот код максимальным (2,n,3) – кодом.
№ варианта |
|
|
№ варианта |
|
1 |
8 |
|
13 |
8 |
2 |
9 |
|
14 |
9 |
3 |
10 |
|
15 |
10 |
4 |
11 |
|
16 |
11 |
5 |
8 |
|
17 |
8 |
6 |
9 |
|
18 |
9 |
7 |
10 |
|
19 |
10 |
8 |
11 |
|
20 |
11 |
9 |
8 |
|
|
|
10 |
9 |
|
|
|
11 |
10 |
|
|
|
Задание № 11
1. Закодировать двоичным кодом Фано алфавит из 10 символов (букв) с заданным распределением вероятностей. Найти среднюю длину полученного кода и сравнить её со средней длиной для равномерного кода.
2. Закодировать троичным кодом Фано алфавит из 10 символов (букв) с заданным распределением вероятностей.
3. Закодировать двоичным кодом Хаффмена алфавит из 10 символов (букв) с заданным распределением вероятностей.
4. Закодировать двоичным кодом Шеннона алфавит из 10 символов (букв) с заданным распределением вероятностей.
Сравнить стоимости (средние длины) двоичных кодов.
1)
2)
3)
4)
5)
6)
7)
8)
9)
10)
11)
12)
13)
14)
15)
16)
17)
18)
Теория графов
Задание № 12
Придумать граф с числом вершин - 8, числом рёбер - 18. Для этого графа найти:
все независимые множества вершин
Все максимальные по включению независимые множества вершин
Все наибольшие независимые множества вершин
Все наибольшие клики
Все наименьшие покрывающие множества вершин
Все наименьшие доминирующие множества вершин
Число вершинной независимости
(G)Кликовое число
Число вершинного покрытия
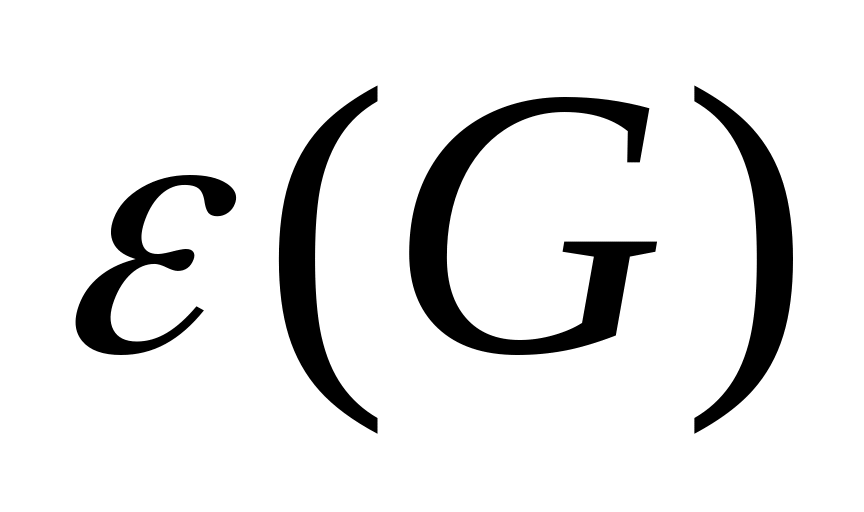
Число доминирования
(G)Все ядра графа
Раскрасить граф
Хроматическое число
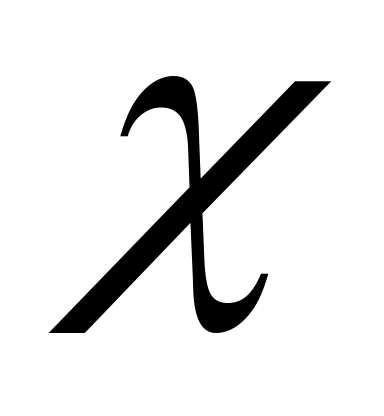(G)
Задание № 13
Построить граф с числом вершин n, числом рёбер l, порядком подгруппы автоморфизмов k.
№ варианта |
(n,l,k) |
|
№ варианта |
(n,l,k) |
1 |
(10,13,2) |
|
13 |
(10,13,5) |
2 |
(9,12,2) |
|
14 |
(9,12,5) |
3 |
(11,14,2) |
|
15 |
(11,14,5) |
4 |
(6,8,2) |
|
16 |
(6,8,6) |
5 |
(10,13,3) |
|
17 |
(9,12,6) |
6 |
(9,12,3) |
|
18 |
(9,6,6) |
7 |
(11,14,3) |
|
19 |
(15,12,6) |
8 |
(6,8,3) |
|
20 |
(13,12,6) |
9 |
(10,13,4) |
|
|
|
10 |
(9,12,4) |
|
|
|
11 |
(11,14,4) |
|
|
|
12 |
(6,8,4) |
|
|
|
Теория расписаний
Задание № 14
Найти оптимальное расписание обработки 3-х деталей на трех станках, расположенных последовательно; - время обработки детали на станке .
№ варианта |
|
1 |
(7, 5, 13, 10, 7, 5, 13, 10, 7) |
2 |
(9, 7, 12, 9, 9, 7, 12, 9, 9) |
3 |
(12, 3, 8, 9, 12, 3, 8, 9, 12) |
4 |
(3, 6, 4, 4, 3, 6, 4, 4, 3) |
5 |
(7, 9, 13, 10, 7, 7, 9, 13, 7) |
6 |
(6, 5, 4, 2, 6, 5, 4, 2, 6) |
7 |
(8, 10, 13, 6, 9, 8, 10, 13, 6) |
8 |
(9, 6, 11, 8, 8, 6, 11, 8, 8) |
9 |
(8, 6, 14, 11, 8, 6, 14, 11, 8) |
10 |
(6, 4, 12, 9, 6, 4, 12, 9, 6) |
11 |
(10, 8, 13, 10, 10, 8, 13, 10, 10) |
12 |
(12, 2, 7, 8, 11, 2, 7, 8, 11) |
13 |
(14, 3, 9, 11, 13, 3, 9, 10, 13) |
14 |
(4, 7, 5, 5, 4, 7, 5, 5, 4) |
15 |
(5, 8, 6, 6, 5, 8, 6, 6, 5) |
16 |
(7, 5, 13, 10, 7, 5, 13, 10, 7) |
Задание № 15
Найти оптимальное расписание обработки 10 деталей на 2 станках, расположенных последовательно; - время обработки детали на станке .
№ варианта |
|
1 |
(2,4,6,12,6,7,8,9,10,2,3,6,8,1,9,12,1,4,6,12) |
2 |
(4,6,8,12,13,2,5,8,5,5,3,9,10,12,14,1,12,3,4,5) |
3 |
(2,6,7,8,9,2,4,12,11,2,3,3,10,11,2,5,7,12) |
4 |
(2,5,6,4,3,8,9,1,1,3,12,11,7,2,1,6,6,2,10,1) |
5 |
(3,6,7,8,2,1,6,6,1,10,3,4,12,3,11,13,1,1,2,6) |
6 |
(6,7,9,12,11,5,8,12,11,10,1,3,4,5,2,11,1,2,11,10) |
7 |
(3,6,7,8,9,1,2,11,3,10,2,2,15,1,3,4,5,2,1,12) |
8 |
(8,9,12,11,3,4,6,2,7,9,11,2,3,1,11,10,3,2,2,3) |
9 |
(4,6,8,9,2,4,7,5,1,9,11,12,11,2,5,7,9,5,5,1) |
10 |
(4,6,7,3,4,8,4,9,2,10,2,4,5,5,1,12,1,4,8,10) |
11 |
(6,4,8,3,10,12,4,7,8,3,12,12,3,7,9,4,4,1,4,10) |
12 |
(5,4,7,9,2,6,4,12,10,1,2,5,8,9,1,12,11,3,6,8) |
13 |
(3,11,2,5,11,10,2,5,7,9,10,12,1,3,1,6,5,3,11,1) |
14 |
(4,6,8,9,3,5,7,12,3,6,45,2,11,2,3,3,11,5,6) |
15 |
(12,5,7,8,9,3,5,11,12,10,2,4,7,2,3,11,12,12,1,4,6) |
Задание № 16
Найти оптимальное периодическое
расписание обработки деталей 5-ти видов
на одном станке.
- среднесуточная трудоёмкость обработки
-ой
детали на станке.
№ варианта |
|
№ варианта |
|
1 |
(9,7,6,2,2) |
13 |
(11,10,9,2,2) |
2 |
(12,6,5,4,4) |
14 |
(14,7,7,5,1) |
3 |
(11,7,6,4,2) |
15 |
(13,9,4,4,2) |
4 |
(10,8,4,4,1) |
16 |
(12,4,4,3,2) |
5 |
(12,5,5,3,1) |
17 |
(15,8,7,5,5) |
6 |
(11,10,3,3,1) |
18 |
(13,5,5,3,2) |
7 |
(9,7,6,5,2) |
19 |
(12,8,6,5,2) |
8 |
(12,6,6,6,5) |
20 |
(11,11,5,3,1) |
9 |
(11,10,9,2,2) |
21 |
(10,5,4,3,2) |
10 |
(13,11,5,4,1) |
22 |
(12,11,3,3,2) |
11 |
(9,9,7,4,2) |
23 |
(13,11,6,1,1) |
12 |
(9,8,4,3,1) |
|
|
Теория алгоритмов
Задание № 17
1) Реализовать на Машине Тьюринга алгоритм
вычисления функции
;
в десятичной системе счисления.
2) Постройте машину Тьюринга, которая бы от натурального числа в десятичной системе счисления отнимала единицу.
3) Реализовать на Машине Тьюринга алгоритм
вычисления функции
;
.
4) Реализовать на Машине Тьюринга алгоритм
вычисления функции
;
в десятичной системе счисления.
5) Постройте машину Тьюринга, которая бы к натуральному числу в десятичной системе счисления прибавляла единицу.
6) Реализовать на Машине Тьюринга алгоритм
вычисления функции
;
в десятичной системе счисления.
7) Реализовать на Машине Тьюринга алгоритм
вычисления функции
;
в десятичной системе счисления.
8) Реализовать на Машине Тьюринга алгоритм
вычисления функции
;
в десятичной системе счисления.
9) Реализовать на Машине Тьюринга алгоритм
вычисления функции
;
в десятичной системе счисления.
10) Реализовать на Машине Тьюринга
алгоритм вычисления функции
;
в десятичной системе счисления.
11) Реализовать на Машине Тьюринга
алгоритм вычисления функции
;
в десятичной системе счисления.
12) Реализовать на Машине Тьюринга
алгоритм вычисления функции
;
в десятичной системе счисления.
13) Реализовать на Машине Тьюринга
алгоритм вычисления функции
;
в десятичной системе счисления.
14) На ленту подряд вписаны два конечных набора единиц, разделенные звездочкой. Составьте программу машины Тьюринга, которая выписывала бы подряд, без разделения звездочкой, столько единиц, сколько их в обоих наборах (сложение единиц).
15) Сконструируйте машину Тьюринга с внешним алфавитом A={a0, 1}, которая каждое слово длиной n в алфавите A1={1} перерабатывает в слово длиной n+1 в том же алфавите A1.