3. Гипербола, её каноническое уравнение, асимптоты Вывод уравнения гиперболы

Определение 10.3. Гиперболой называется геометрическое место точек, разность расстояний от которых до двух данных точек, называемых фокусами, есть величина постоянная.

Эту постоянную величину обозначим через 2а, расстояние между фокусами - через 2с, для гиперболы 2с > 2а.

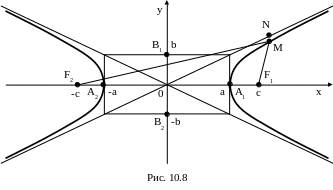
Через фокусы F₁ и F₂ проведем ось абсцисс. Перпендикулярно к середине отрезка [F₁ F₂] проведем ось ординат (рис. 10.8).

Пусть М(х; у) – любая точка гиперболы. Тогда

| F₁ M| = , |F₂ M| = .

По определению гиперболы |F₂ M| – |F₁ M| = 2a. Подставляя сюда выражения для |F₂ M| и |F₁ M|, получим

.

Для последующего упрощения этого уравнения запишем его в виде

и возведём в квадрат обе части полученного уравнения:

.

После приведения подобных получим

.

Возведём левую и правую части этого уравнения в квадрат:

=

= . (10.3)

Так как с > a, введем обозначение .

Уравнение (10.3) при этом примет вид

После его почленного деления на a²b²  0 получим

. (10.4)

Уравнение (10.4) называется каноническим уравнением гиперболы.

Исследование формы гиперболы по ее уравнению

1. Симметрия гиперболы. В уравнение гиперболы текущие координаты входят только во второй степени, потому оси координат являются осями симметрии гиперболы. Ось симметрии, на которой расположены фокусы, называется фокальной осью. Точка пересечения осей симметрии называется центром гиперболы.

2. Точки пересечения с осями симметрии (если они существуют) называются вершинами гиперболы. Полагая y = 0, получим , отсюда х =  a, значит, вершинами гиперболы являются точки А₁(а, 0) и А₂(-а, 0); А₂А₁ = 2a. При x = 0 получаем , отсюда y =  b , т.е. для величины y мы получим мнимые значения. Это означает, что гипербола не пересекает ось Оy.

На оси ординат отложим точки B₁(0, b) и B₂(0,-b). Отрезок |B₁ B₂| длиной 2b называются мнимой осью гиперболы.

На оси Оx отложим точки A₁(a, 0) и A₂(-a; 0). Отрезок |A₁ A₂| = 2а называются действительной осью гиперболы, a - действительная, b - мнимая полуоси гиперболы.

3. Форма гиперболы. Ввиду симметрии рассмотрим только часть гиперболы при x > 0 и y > 0.

Из уравнения видно, что , т.е. a  x  +.

Когда x увеличивается от a до + , то величина y тоже растет от 0 до + , значит, кривая расположена вне полосы, ограниченной прямыми x=  a.

4. Асимптоты гиперболы. Построим так называемый основной прямоугольник, стороны которого проходят через точки А₁, А₂, В₁, В₂ параллельно осям координат. Проведём его диагонали и продолжим их. Полученные прямые называются асимптотами гиперболы. Их уравнения: y =  .

Покажем, что при x   расстояние между гиперболой и асимптотой стремится к нулю. Возьмём две точки с одинаковой абсциссой x, лежащих на прямой N(x, y_n) и на гиперболе M(x, y₂).

Расстояние между ними при x  :

при х   |MN|  0.

5. Эксцентриситет гиперболы. Так как с² = а² + b², то . Чем больше эксцентриситет, тем больше угол между асимптотами:

с =  а; с² = а² + b²; а² (² – 1) = b²; .

При а = b гипербола называется равносторонней: х² – у² = а².

Угловые коэффициенты ее асимптот , следовательно, асимптоты перпендикулярны между собой.