24

Занятие 2.2. КРИВЫЕ ВТОРОГО ПОРЯДКА

На предыдущей лекции мы увидели, что всякое алгебраическое уравнение первой степени с двумя переменными Ах + Ву + С = 0 на плоскости R² в декартовой прямоугольной системе координат определяет прямую линию. В связи с этим прямую называют алгебраической линией 1-го порядка. Алгебраическое уравнение второй степени с двумя переменными имеет вид

Ах² + Вху + Су² + Dх + Еу + F = 0.

Линии, определяемые такими уравнениями, получили название алгебраических линий второго порядка. Линии второго порядка мы будем рассматривать на данной лекции.

Конические сечения

Краткий опрос по основным понятиям, изложенным в предыдущей лекции:

1. Какое уравнение называется векторным уравнением прямой?

2. Какое уравнение называется скалярным уравнением прямой?

3. Какое уравнение называется общим уравнением прямой?

4. Какое уравнение называется каноническим уравнением прямой?

5. Какое уравнение называется уравнением прямой с угловым коэффициентом?

6. Какое уравнение называется уравнением прямой проходящей через две точки?

7. Каково условие параллельности двух прямых?

8. Каково условие перпендикулярности двух прямых?

Можно доказать, что кривые второго порядка получаются при пересечении плоскостями так называемой конической поверхности, образованной вращением прямой (она называется образующей конуса) вокруг оси вращения, имеющей с образующей общую точку О (рис. 10.1).

Е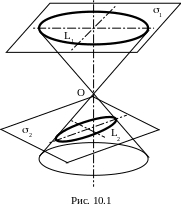 сли секущая плоскость проходит через ось вращения, то в сечении получится пара прямых. Если секущая плоскость пересекает только одну полость конуса, то в сечении получаются замкнутые кривые.

При этом, если секущая плоскость перпендикулярна оси конуса (плоскость ₁), то очевидно, что линия сечения L₁ представляет собой окружность.

При "небольшом" наклоне секущей плоскости (плоскость ₂), пока угол между перпендикуляром к секущей плоскости и осью конуса меньше половины вершинного угла конуса, получаем замкнутую линию L₂, называемую эллипсом (иногда – овалом).

При дальнейшем повороте секущей плоскости, с увеличением угла между перпендикуляром к секущей плоскости и осью конуса, получится, что секущая плоскость пересечет обе полости конуса (плоскость ₃ на рис. 10.2, а). В таком случае в сечении будем иметь кривую L₃, состоящую из двух ветвей и называемую гиперболой.

Н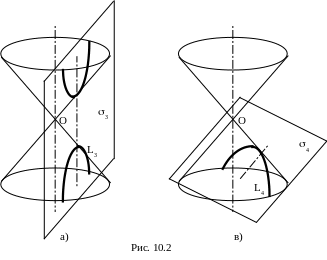 а рис. 10.2,в показано так называемое "критическое" положение секущей плоскости (плоскость ₄), когда она параллельна одной из образующих конуса. Кривая L₄, получаемая таким образом, называется параболой.

1. Окружность, ее каноническое уравнение

Определение 10.1. Окружностью называется геометрическое место точек на плоскости, равноудаленных от одной, называемой ее центром.

Составим уравнение окружности с центром в точке C(a, b) и радиусом R. Возьмём на плоскости любую точку M(x, y) (рис. 10.3). Если точка M(x, y) лежит на окружности, то расстояние |CM| = R. Используем формулу для определения расстояния между двумя точками:

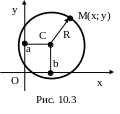= R или

(x - a)² + (y - b)² = R² – каноническое уравнение окружности.

Рассмотрим уравнение окружности в полярных координатах.

П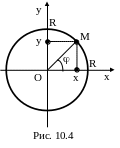 усть дано уравнение окружности x² + y² = R² в декартовых координатах (центр окружности совпадает с началом координат, рис. 10.4).

Найдём уравнение окружности в полярных координатах. Подставив в уравнение окружности

x = cos, y = sin, получим:

²cos² + ²sin² = R,  ²(cos² + sin²) = R², 

² = R², или  = R - уравнение окружности в полярных координатах.

Остановимся на уравнении окружности в параметрической форме. Текущие координаты точки, лежащей на окружности, являются функциями угла , образованного радиусом окружности R с положительным направлением оси Oх. Примем  за переменный параметр и выразим через него текущие координаты x и y:

Получили параметрические уравнения окружности.

Пример 10.1. Построить линию, заданную уравнением:

.

Решение. Выразим у из уравнения .

Отсюда видно, что у  0, т.е. график расположен не выше оси Ох. Избавимся от корня в полученном уравнении, для чего возводим во вторую степень обе его части:

у² = 6х – х²,  х² - 6х + у² = 0.

В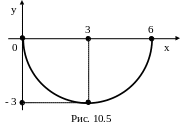 ыделяем полный квадрат для х:

х² - 6х + 9 – 9 + у² = 0, 

 (х – 3)² + у² = 9.

Таким образом, получили уравнение окружности с центром в точке С(3, 0) и радиусом R = 3. Учитывая, что у  0, строим нижнюю половину окружности (рис. 10.5).

Вопросы на понимание основных понятий:

1. Что называется окружностью?

2. Какое уравнение называется каноническим уравнением окружности?

3. Какое уравнение называется уравнением окружности в полярных координатах?

4. Какие уравнения называются параметрическими уравнениями окружности?