2. Содержание и структура работы:

Работа должна состоять из введения, основной части, заключения и списка использованных информационных источников. Основная часть работы может составлять 80-120 страниц, шрифт TimesNewRoman, размер 14, интервал 1,5.

Во введении должны содержаться основные характеристики работы.

Основная часть – это результаты Ваших исследований.

В заключении приводятся общие выводы по результатам исследований (от 3 до 8). Выводы не должны дублировать результаты, но с другой стороны – полностью соответствовать результатам исследований и вытекать из них.

Основная часть должна состоять из разделов, подразделов, а также может содержать пункты и подпункты. Например:

Раздел 1. Анализ источников по теме исследований.

1.1 Анализ технологий… (название, исходя из темы)

1.2 Анализ оборудования… (название, исходя из темы)

1.3 Анализ материалов… (название, исходя из темы)

Первый раздел, как правило, должен быть посвящен анализу известных результатов по теме исследований.

Второй раздел, обычно, посвящен общей методике (алгоритму действий для достижения цели исследований) и методам решения отдельных задач. Начинают его с обоснования направления исследований и формулировки научной гипотезы. Общую методику проще и нагляднее представить в форме блок-схемы исследований. В общем виде она показана на рис. 1, однако, каждый магистр должен ее конкретизировать в соответствии с темой, целью и задачами своих исследований.

Третий раздел должен содержать результаты исследований. Он является основным во всей работе.

Четвертый раздел может быть посвящен эффективности результатов исследования, результатам апробации (на строительной площадке, на конференции) и внедрению результатов. Здесь же могут быть технологический регламент, рекомендации, технологические карты.

В зависимости от выбранного направления и формы выпускной магистерской работы содержание ее может быть изменено. Выше приведены рекомендации для наиболее распространенной первой формы магистерской работы – экспериментальной. Но и для других форм, по возможности, необходимо соблюдать представленные рекомендации. Магистр имеет право несколько изменить структуру и содержание работы, по согласованию со своим руководителем выпускной магистерской работы. До согласования плана-проспекта с руководителем не имеет смысла начинать написание работы.

4. Использование теории планирования экспериментов для исследований в работе

Математическое моделирование – это средство изучения реального объекта, процесса или системы путем их замены математической моделью, более удобной для экспериментального исследования с помощью компьютера.

Математическая модель является приближенным представлением реальных объектов, процессов или систем, выраженным в математических терминах и сохраняющим существенные черты оригинала. Математические модели в количественной форме, с помощью логико-математических конструкций, описывают основные свойства объекта, процесса или системы, его параметры, внутренние и внешние связи.

Построение математической модели заключается в определении связей между теми или иными процессами и явлениями, создании математического аппарата, позволяющего выразить количественно и качественно связь между данными процессами и явлениями, между интересующими специалиста физическими величинами, и факторами, влияющими на конечный результат.

Выбор типа модели зависит от наших знаний об объекте, целей исследования и математического аппарата. В данных методических рекомендациях будет рассматриваться экспериментально-статистическое (ЭС) моделирование. Данный вид моделей относится к стохастическим, т.е. учитывающим случайный характер процессов в исследуемых объектах и системах, который описывается методами теории вероятности и математической статистики.

При построении математической модели перед исследователем возникает задача выявить и исключить из рассмотрения факторы, несущественно влияющие на конечный результат. Математическая модель обычно включает значительно меньшее число факторов, чем в реальной действительности.

Под планированием эксперимента понимается процедура выбора числа опытов и условий их проведения, необходимых для решения поставленной задачи с требуемой точностью. Все факторы изменяются одновременно по специальным правилам, а результаты эксперимента представляются в виде математической модели.

Входные переменные – факторы определяют состояние объекта. Основное требование к факторам – управляемость, т.е. возможность установки нужного значения (уровня) фактора и поддержания его в течение всего опыта. В этом состоит особенность активного эксперимента.

Выходные переменные – показатели или отклики – это важные для целей эксперимента реакции на воздействие входных переменных.

Отклики обозначаются как Y₁, Y₂, …Y_n, а факторы – как X₁, X₂, ….X_n.

Таким образом, объект исследования (управляемую систему) можно описать, используя терминологию «черного ящика», которая схематически изображена на рис.1.

Рис.1. Принципиальная схема исследования управляемой системы.

Для проведения эксперимента необходимо иметь возможность воздействовать на входные факторы (Х_i), т.е. на входы «черного ящика», а также по возможности необходимо исключить и/или стабилизировать возмущающие воздействия среды.

Таким образом, математической моделью является уравнение, связывающее отклик с факторами. Это уравнение в общем виде можно записать так:

Y =  (X₁, X₂…X_n)

Каждый фактор X_i в силу объективных причин существует лишь в некотором диапазоне, а в эксперименте приминается в определенных границах, называемым размахом варьирования: X_i.min < X_i < X_i.max . Половина размаха носит назва­ние интервала варьирования Х_i, а середина диапазона варьирования Х_0i – основного уровня фактора:

Х_i=0.5(X_i.max – X_i.min)

Х_0i=0.5(X_i.max + X_i.min)

При экспериментально-статистическом моделировании целесо­образно (как со статистической и вычислительной позиций, так и с точки зрения интерпретации) переходить от натуральных переменных (именованные величины с размерно­стью) к безразмерным нормализованным переменным:

x_i=(X_ix – X_0i)/Х_i

При нормализации факторов нивелируется значение масштаба диапазона фактора (например, финансирование может изменяться в пределах тисяч или миллионов грн., а объемы работ – в пределах 10 п.м или 1000м²) и происходит центрирование переменных в результате переноса начала координат в точку X_0i.

Каждый фактор может принимать в опыте одно из нескольких значений. Эти значения называются уровнями. В эксперименте фактор должен иметь определенное число дискретных уровней.

Если Х_i= X_i.min , то x_i= –1, если Х_i= X_0i , то x_i= 0 , если Х_i= X_i.max , то x_i= 1.

Фиксированный набор уровней факторов определяет одно из возможных состояний «черного ящика». Если перебрать все возможные наборы состояний, то получается множество различных состояний «черного ящика». Одновременно это будет число возможных различных опытов. Число возможных опытов (N) определяют по выражению:

N = pⁿ

где: р – число уровней; n – число факторов.

Для построения исключительно линейных зависимостей достаточно двухуровневого эксперимента (p = 2), поскольку уравнение прямой пропорциональности можно получить по 2-м точкам в пространстве. Соответственно при исследовании одного фактора N = 2¹. В технике, в том числе в строительстве, большинство зависимостей носят нелинейный характер. Для получения степенной функции второго порядка вида Y=b₀+b₁x+b₁₁x² достаточно трех точек, соответственно при исследовании одного фактора N = 3¹. В дальнейшем в данных методических рекомендациях мы будем рассматривать только трехуровневое варьирование факторов.

Применение аппарата ЭС-моделирования становится оправдано только с 2-х и более факторных задач, поскольку при исследовании влияния одного фактора достаточно легко проследить тенденции и сделать выводы без построения моделей, а при необходимости возможно применение более простых математических методов. Соответственно при исследовании влияния 2-х факторов с 3-х уровневым варьировании факторов полный факторный план эксперимента будет иметь 9 точек (N = 3²).

Таким образом, построение наиболее простых планов сводится к выбору экспериментальных точек, симметричных относительно центра эксперимента. В этом случае все n факторов изменяются на трех уровнях, и план эксперимента является полным факторным планом типа 3ⁿ. Уровни факторов изображаются тремя точками на каждой из n координатных осей факторного n-мерного пространства. Эти уровни симметричны относительно основного уровня. Один из них – минимальный, второй – средний, третий – максимальный (рис.2).

В качестве примера рассмотрим задачу исследования влияния на продолжительность монтажа этажа на неком объекте двух факторов:

Х₁ – количества башенных кранов, установленных на объекте, от 5 до 15 штук;

Х₂ – количества рабочих, работающих на объекте, от 100 до 200 человек;

Рис.2. Полный факторный план 2-х факторного эксперимента типа 3².

В кодированном виде факторы х₁ и х₂ будет изменяться в диапазоне от –1 до +1 и пересчитываться по описанной выше методике. Соответственно при Х₁ = 5 (кранов) кодированное значение фактора будет равно х₁ = –1; при Х₁ = 10 (кранов) х₁ = 0, а при Х₁ = 15 (кранов) х₁ = +1. Аналогично кодируется фактор Х₂. То есть таблица плана эксперимента в этом случае будет иметь следующий вид (Таблица 2):

Таблица 2

Пример таблицы полного факторного плана 2-х факторного эксперимента

№	Натурные переменные		Кодированные переменные		Y, время монтажа этажа (дней)
	Х1, количество кранов (шт)	Х2 количество рабочих (человек)	х1, количество кранов	х2, количество рабочих
1	5	100	-1	-1	26
2	5	150	-1	0	24
3	5	200	-1	1	22
4	10	100	0	-1	22
5	10	150	0	0	15
6	10	200	0	1	13
7	15	100	1	-1	19
8	15	150	1	0	14
9	15	200	1	1	11

В результате расчета ЭС-модели мы должны получить полином следующего вида:

Y = b₀ + b₁x₁ + b₁₁x₁² + b₁₂x₁x₂

+ b₂x₂ + b₂₂x₂²

Расчет модели можно выполнять с использованием программы Compex, разработанной в ОГАСА на кафедре ПАТСМ под руководством проф. В.А. Вознесенского [1,2]. Для корректной работы старых версий Compex в операционных системах Windows XP, Windows 7 и более новых необходимо пользоваться эмуляторами DOS, например dosbox.

Расчет выполняем в такой последовательности:

Ввод данных – факторы – количество – вводим «2»

Ввод данных – факторы – наименование – ввод нового наименования – вводим «краны» или «krany» или просто х₁, далее «рабочие» или «rabochie» или просто х₂.

Ввод данных – план – клавиатура – число строк – вводим «9»

Ввод данных – план – клавиатура – ввод – вводим матрицу эксперимента в нормализованном виде. Сохранить – да или нет на выбор.

Ввод данных – вид модели – клавиатура – стандартный – сохранить - нет.

Ввод данных – отклики – наименование – Ввод нового наименования – вводим «время_монтажа» или «vremya» или просто Y.

Ввод данных – отклики – ввод – клавиатура – вводим девять значений времени монтажа.

Моделирование – степень риска – вводим 0.2. Это уровень двустороннего риска при подсчете модели – 20%, это означает, что односторонний риск равен 10%.

Моделирование – ошибка эксперимента – вводим примерно 1% от среднего значения выхода, в данном случае можно ввести 0.2.

Моделирование – Расчет модели. Этот расчет следует выполнить три-четыре раза, пока критерий Фишера не совпадет с критическим, то есть когда Критерий Fisher = Критерий Fkr.

Описание методов расчета коэффициентов ЭС-моделей не входит в цели рассмотрения данных методических рекомендаций и при необходимости их изучения необходимо обратится к специальной литературе [2-4].

Ниже приведен пример расчета рассматриваемой ЭС-модели.

Уровень риска = 0.200

Критерий Studenta= 1.282

Ошибка эксперимента(Ts)э = 1.038

─────────────────────────────────────────

N Коэффициенты Ts

─────────────────────────────────────────

1 b0 = 15.889 ( 21.317 )

2 b1 = -4.667 ( 11.431 )

3 b2 = -3.500 ( 8.573 )

4 b11 = 2.667 ( 3.771 )

5 b22 = 1.167 ( 1.650 )

6 b12 = -1.000 ( 2.000 )

─────────────────────────────────────────

N YE Y DELT DELT**2

─────────────────────────────────────────

1 26.000 26.889 -0.889 0.790

2 24.000 23.222 0.778 0.605

3 22.000 21.889 0.111 0.012

4 22.000 20.556 1.444 2.086

5 15.000 15.889 -0.889 0.790

6 13.000 13.556 -0.556 0.309

7 19.000 19.556 -0.556 0.309

8 14.000 13.889 0.111 0.012

9 11.000 10.556 0.444 0.198

─────────────────────────────────────────

Суммы по строкам 0.000 5.111

Число степеней свободы эксперимента 3

Ошибка эксперимента 0.8095

Дисперсия неадекватности 1.7037

Ошибка неадекватности 1.3053

Критерий Fisher = 2.6000 Критерий Fkr = 2.6000

Kzm = 1.000 NSe = 0.809

Таким образом, полученную в примере ЕС-модель можно записать так:

Y(дней) = 15.89 – 4.67x₁ + 2.67x₁² – 1.00x₁x₂

– 3.50x₂ + 1.17x₂²

Далее наиболее информативным является построение диаграммы в виде квадрата. Для этого в программе Compex выполняем следующее:

Интерпретация – двухмерная – факторы для номограмм – по горизонтали – выбираем «х₁» – по вертикали – выбираем «х₂».

Интерпретация – двухмерная – выбор уровней – пользователем.

Интерпретация – двухмерная – выбор уровней – количество.

Далее следует подобрать количество и шаг изолиний на будущей диаграмме таким образом, чтобы их было от 3-х до 8-ми (желательно - 4...6) и чтобы изолинии располагались с равным шагом. Причем наименьшей уровень изолинии должно быть чуть больше минимального значения выхода, полученного в ЕС-модели, а наибольший уровень изолинии - чуть меньше максимального значения выхода. В примере выбираем 8 изолиний (рис.3).

Интерпретация – двухмерная – выбор уровней – уровни – и задаем выбранные уровни для изолиний.

Далее Интерпретация – двухмерная – построение изолиний.

Рис.3. Пример построения диаграммы по 2-х факторной модели в программе Compex.

Более наглядно диаграмму по полученной ЭС-модели можно построить с офисном приложении Ecxel, однако это требует некоторых дополнительных навыков (рис.4).

Анализ полученных ЭС-моделей и диаграмм не входит в цели рассмотрения данных методических рекомендаций и при необходимости ознакомится с методикой его проведения необходимо обратится к специальной литературе [2-5].

Следует обратить внимание, что в рассмотренном примере выполнялся 2-х факторный эксперимент, т.е. влияние прочих возможных воздействий стабилизировалось. На практике же чаще всего представляет интерес рассмотрение задач, в которых варьируется 3, 4 и более факторов. Соответственно возрастает число экспериментов, которые необходимо проводить. Например, для построения 3-х факторной ЭС-модели при использовании полного факторного плана эксперимента необходимо провести 27 экспериментов (точек плана), т.е. N = 3³ (рис.4).

Рис.4. Пример построения диаграммы по 2-х факторной модели

в офисном приложении Excel.

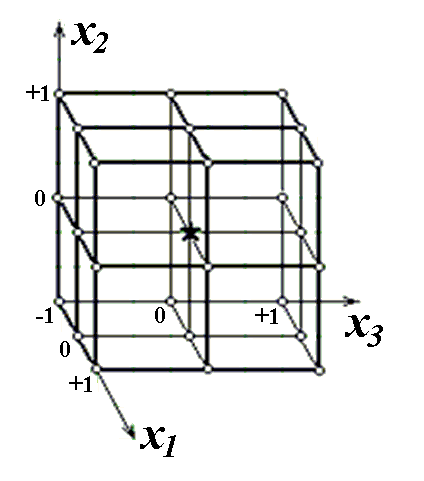
Рис.5. Полный факторный план 3-х факторного эксперимента типа 3³.

Количество опытов в полном факторном эксперименте значительно превосходит число определяемых коэффициентов ЭС-модели. Другими словами, полный факторный эксперимент обладает некоторой избыточностью опытов, а проведение каждого требует определенных затрат. Было бы заманчивым сократить их число за счет той информации, которая не очень существенна при построении моделей выбранного типа. При этом нужно стремиться к тому, чтобы матрица планирования не лишилась бы своих оптимальных свойств.

Рассмотрим вышеизложенный пример. Теперь будем изменять 3 фактора. Первые два совпадают с первой задачей:

Х₁ – количества башенных кранов, установленных на объекте, от 5 до 15 штук;

Х₂ – количества рабочих, работающих на объекте, от 100 до 200 человек.

Вводим третий:

Х₃ – продолжительность рабочего для, от 8 до 12 часов.

Таблица полного факторного эксперимента (27 точек) будет иметь вид (Таблица 2):

Таблица 2

Пример таблицы полного факторного плана 3-х факторного эксперимента

№	Х1	Х2	Х3	х1	х2	х3	Монтаж (дней)
	кранов, шт	рабочих, чел	рабочий день, ч.	кранов	рабочих	рабочий день
1	5	100	8	-1	-1	-1	26
2	5	150	8	-1	0	-1	24
3	5	200	8	-1	1	-1	22
4	10	100	8	0	-1	-1	22
5	10	150	8	0	0	-1	15
6	10	200	8	0	1	-1	13
7	15	100	8	1	-1	-1	19
8	15	150	8	1	0	-1	14
9	15	200	8	1	1	-1	11
10	5	100	10	-1	-1	0	22
11	5	150	10	-1	0	0	19
12	5	200	10	-1	1	0	18
13	10	100	10	0	-1	0	17
14	10	150	10	0	0	0	13
15	10	200	10	0	1	0	11
16	15	100	10	1	-1	0	16
17	15	150	10	1	0	0	12
18	15	200	10	1	1	0	9
19	5	100	12	-1	-1	1	20
20	5	150	12	-1	0	1	18
21	5	200	12	-1	1	1	16
22	10	100	12	0	-1	1	16
23	10	150	12	0	0	1	12
24	10	200	12	0	1	1	10
25	15	100	12	1	-1	1	14
26	15	150	12	1	0	1	11
27	15	200	12	1	1	1	8

По данной таблице описанными выше методами можно построить следующую ЭС-модель:

Y(дней) = 13.19 – 3.94x₁ + 2.28x₁² – 0.75x₁x₂ + 0.58x₁x₃

– 3.00x₂ + 0.78x₂² + 0.42x₂x₃

– 2.28x₃ + 0.94x₃²

Таким образом, в примере нами была получена ЭС-модель с 10-ю оценками коэффициентов b_i при реализации 27-ми точечного плана. Как отмечалось выше, актуальна задача сокращения числа необходимых экспериментов (натурных, вычислительных и пр.).

Решение задачи оптими­зации эксперимента, вообще говоря, традиционно в истории нау­ки и техники. Их постановка всегда приводила исследователей к необходимости как-то планировать свою экспериментальную дея­тельность с учетом уже накопленного опыта. Создание математической теории эксперимента (МТЭ) позволило рассматривать и решать проблемы такого планирования через оптимальность математических моделей, описывающих объек­ты в соответствии с целями исследования, проектирования и управ­ления ими.

Развитие МТЭ позволило определить некоторые основные принципы оптимального пла­нирования эксперимента.

Во-первых, из системы нормальных уравнений для определения L неизвестных оценок b_i в ЭС-модели следует, что необходимо и достаточно, чтобы матрица эксперимента содержала L разных строк. Сле­довательно, минимальное число опытов в плане N_min = L (так называемый насыщенный план), а избыточность опытов N > L полезна не с алгебраической, а со статистической точки зрения.

Во-вторых, вид матрицы эксперимента определяет не только численные значения неизвестных оценок коэффициентов модели, но и характеристики точности модели как в целом, так и отдельных ее параметров. Например, диагональные элементы матрицы эксперимента оценивают дисперсии оценок каждого коэф­фициента, следовательно, точность оценок будет различной, если эти элементы не равны между собой. Внедиагональные эле­менты определяют корреляцию оценок коэффициен­тов модели. Кроме того, исключение (добавление) некоторого эффекта b_i в ЭС-модель для уточнения формы связи между откликом системы и факторами приводит к пересчету всех остав­шихся оценок коэффициентов.

В-третьих, вид матрицы эксперимента не зависит от результатов эксперимента и, следовательно, матрица может быть исследована до его реализации. Результаты такого анализа могут служить основой для конструирования матрицы плана некоторым оптимальным (о точки зрения целей всего исследования системы) образом до проведения опытов. Априори можно исследовать и меру точности предсказания выхода, связан­ную только с расположением опытных точек, использовать результаты анализа для повышения точности модели и т.п.

Исследование матриц, мер их точности и других статистических характеристик с целью конструирования матриц плана и есть одно из основных направлений оптимального алгоритмизированного планирования эксперимента.

Оптимальность оценивается по большому числу критериев, каждый из которых приобретает ту или иную ценность для экспериментатора в зависимости от це­лей его исследований. Эти критерии в абстрактной математической форме обобщают ту массу пожеланий, которые экспериментатор выдвигает к результатам своих исследований на профессионально-логическом уровне («Нужно как можно точнее оценить координа­ты минимальной продолжительности строительства», «Влияние всех факторов должно оцениваться с одинаковой точностью» и т. п.). При этом всегда важным показателем для любого плана эксперимента является количество строчек – т.е. количество экспериментов, которые необходимо поставить исследователю для построения ЭС-модели. Возможно, что тре­бования к плану эксперимента будут противоречивы, однако МТЭ позволяет построить планы, достаточно хорошие с позиций разных критериев (планы, близкие к оптимальным).

Данные планы создаются специалистами в области МТЭ и описаны в специальной литературе. Для прикладных исследований, в том числе в области строительства, в подавляющем большинстве случаев достаточно правильно выбрать один из готовых планов эксперимента с заданным числом факторов, удовлетворяющих исследователя по точности и количеству необходимых опытов (точек).

Ниже из большого числа известных и отработанных планов эксперимента приводятся те, которые имеют наибольшее распространение в прикладных областях, в частности в технологии строительства.

Для приведенного выше примера 3-х факторной задачи (табл.2) теоретически возможно снижение числа строк (точек) плана до 10-ти. Однако такие насыщенные планы всегда имеют низкую точность. Наиболее же оптимальным для большинства 3-х факторных задач является 15-ти точечный симметричный план. Он получен путем сокращения 12-ти точек из полного факторного плана. Однако необходимо отметить, что это не единственный метод получения оптимальных планов, например, существует метод размещения точек на сфере, вписанной в факторное пространство эксперимента. Более подробно это вопрос описан в специальной литературе [3-5]. В частности, в книге [5] приведено большинство отработанных планов многофакторных экспериментов.

В таблице 3 приведен пример рассматриваемого нами 3-х факторного эксперимента при использовании 15-ти точечного плана.

По данной таблице методами, аналогичными построению модели по таблице 2 (27 точек) была получена следующая ЭС-модель:

Таблица 3.

Пример 15-точечного плана 3-х факторного эксперимента

№	Х1	Х2	Х3	х1	х2	х3	Монтаж (дней)
	кранов, шт	рабочих, чел	рабочий день, ч.	кранов	рабочих	рабочий день
1	5	100	8	-1	-1	-1	26
2	5	200	8	-1	1	-1	22
3	10	150	8	0	0	-1	15
4	15	100	8	1	-1	-1	19
5	15	200	8	1	1	-1	11
6	5	150	10	-1	0	0	19
7	10	100	10	0	-1	0	17
8	10	150	10	0	0	0	13
9	10	200	10	0	1	0	11
10	15	150	10	1	0	0	12
11	5	100	12	-1	-1	1	20
12	5	200	12	-1	1	1	16
13	10	150	12	0	0	1	12
14	15	100	12	1	-1	1	14
15	15	200	12	1	1	1	8

Y(дней) = 13.00 – 3.90x₁ + 2.50x₁² – 0.75x₁x₂ + 0.50x₁x₃

– 2.80x₂ + 1.00x₂² + 0.25x₂x₃

– 2.30x₃ + 0.50x₃²

Как видно из примера, данная ЭС-модель, полученная за счет анализа данных эксперимента, проведенного по 15-ти точечному плану, практически не отличается от ЭС-модели, полученной при реализации 27-ми точечного плана.

Наилучшим (наиболее полным) графическим отображением данной ЭС-модели является диаграмма в виде куба с расположенными в его пространстве изоповерхностями, отображающими влияние вирируемых факторов по выход Y, в данном случае – продолжительность монтажа. Пример построенной по приведенной выше ЭС-модели диагаммы приведен на рис.5.

Рис. 6. Пример диаграммы в виде куба, построенной по 3-х факторной ЭС-модели.

Задача оптимального планирования эксперимента становится еще более очевидной с ростом числа факторов в эксперименте. Так для реализации полного факторного эксперимента при варьировании 4-х факторов необходима 81 точка (3⁴). За счет оптимального планирования для получения квадратичных ЭС-моделей вида

Y = b₀ + b₁x₁ + b₁₁x₁² + b₁₂x₁x₂ + b₁₃x₁x₃ + b₁₄x₁x₄

+ b₂x₂ + b₂₂x₂² + b₂₃x₂x₃ + b₂₄x₂x₄

+ b₃x₃ + b₃₃x₃² + b₃₄x₃x₄

+ b₄x₄ + b₄₄x₄²

достаточно применение, например 18-ти или 25-ти точечного плана (таблица 4).

Полный факторный эксперимент при варьировании 5 факторов содержит уже 243 точки (3⁵). За счет оптимального планирования для получения квадратичных ЭС-моделей достаточно реализовать эксперимент по специальному 27-ми точечному плану, пример которого приведен в таблице 5. Аналогично, 6-ти факторный эксперимент можно с достаточной степенью точности реализовать по 35-ти или 40-ка точечному плану, хотя полный факторный эксперимент при варьировании 6-ти факторов включает 729 точек.

Таблица 4.

Примеры 18-ти и 25-ти точечных 4-х факторных планов эксперимента.

№ Уровни факторов x1 x2 x3 x4 1 0 0 0 0 2 -1 -1 1 -1 3 -1 1 -1 1 4 1 -1 -1 1 5 1 1 1 1 6 1 1 -1 -1 7 0 1 1 -1 8 0 -1 -1 -1 9 0 -1 1 1 10 1 0 1 -1 11 -1 0 -1 -1 12 -1 0 1 1 13 1 -1 0 -1 14 -1 1 0 -1 15 -1 -1 0 1 16 1 -1 1 0 17 -1 1 1 0 18 -1 -1 -1 0

№ Уровни факторов x1 x2 x3 x4 1 1 1 1 1 2 1 1 1 -1 3 1 1 -1 1 4 1 1 -1 -1 5 1 -1 1 1 6 1 -1 1 -1 7 1 -1 -1 1 8 1 -1 -1 -1 9 -1 1 1 1 10 -1 1 1 -1 11 -1 1 -1 1 12 -1 1 -1 -1 13 -1 -1 1 1 14 -1 -1 1 -1 15 -1 -1 -1 1 16 -1 -1 -1 -1 17 1 0 0 0 18 -1 0 0 0 19 0 1 0 0 20 0 -1 0 0 21 0 0 1 0 22 0 0 0 1 23 0 0 -1 0 24 0 0 0 -1 25 0 0 0 0

Таблица 5.

Пример 27-ми точечного 5-ти факторного плана эксперимента.

№	Уровни факторов
	x1	x2	x3	x4	x5
1	1	1	1	1	-1
2	1	1	1	-1	1
3	1	1	-1	1	1
4	1	1	-1	-1	-1
5	1	-1	1	1	1
6	1	-1	1	-1	-1
7	1	-1	-1	1	-1
8	1	-1	-1	-1	1
9	-1	1	1	1	1
10	-1	1	1	-1	-1
11	-1	1	-1	1	-1
12	-1	1	-1	-1	1
13	-1	-1	1	1	-1
14	-1	-1	1	-1	1
15	-1	-1	-1	1	1
16	-1	-1	-1	-1	-1
17	1	0	0	0	0
18	-1	0	0	0	0
19	0	1	0	0	0
20	0	-1	0	0	0
21	0	0	1	0	0
22	0	0	-1	0	0
23	0	0	0	1	0
24	0	0	0	-1	0
25	0	0	0	0	1
26	0	0	0	0	-1
27	0	0	0	0	0

Таким образом, за счет оптимального планирования эксперимента возможно значительно сократить число необходимых натурных или вычислительных исследований для получения достоверных ЭС-моделей, позволяющих комплексно проанализировать изучаемую систему или объект. Применение методов планирования эксперимента является мощным методом повышения эффективности и достоверности научных изысканий, в том числе в технологии и организации строительного производства.