1. Элементы векторной алгебры
1.1. Основные понятия и определения
Вектором называется направленный отрезок, который можно перемещать параллельно самому себе (рис. 1.1).
В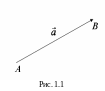
ектор
обозначается либо одной, либо двумя
буквами со стрелкой сверху:
Во втором случае точки А и В являются
началом и концом вектора соответственно.
Длиной
вектора
называется длина отрезка АВ. Если два
вектора имеют одну и ту же длину и
направление, то они представляют из
себя один и тот же вектор и называются
равными.
Если
начало и конец вектора совпадают, то
такой вектор называется нулевым и
обозначается
.
Длина такого вектора равна нулю, а
понятие направления для него не имеет
смысла.
Вектор,
длина которого равна единице в выбранной
системе единиц, называется единичным
и, как правило, обозначается
.
В
екторы,
лежащие на одной или на параллельных
прямых, называются коллинеарными.
Суммой двух векторов является вектор, совпадающий с диагональю параллелограмма, построенного на этих двух векторах, выходящих из одной общей точки (рис. 1.2).
Операция сложения векторов обладает следующими свойствами:
1.
2.
Для
любого вектора существует противоположный
вектор по отношению к нему, который
обозначается
имеющий ту же длину и противоположное
направление. Сумма
Сложение
произвольного вектора с нулевым вектором
дает нулевой вектор:
Разностью
двух векторов
и
называется такой вектор
,
что
(рис. 1.3). Очевидно, что разность векторов
есть сумма первого вектора и вектора,
противоположного второму:
П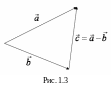
роизведением
вектора на действительное число
называется вектор
,
длина которого
,
а направление совпадает с направлением
вектора
,
если
> 0, и противоположно вектору
,
если
< 0.
Операция произведения вектора на число обладает следующими свойствами:
1.
2.
3.
4.
5.
Справедлива следующая теорема. Два ненулевых вектора и коллинеарны тогда и только тогда, когда выполняется равенство:
Нулевой вектор коллинеарен любому вектору.
Важным понятием в аналитической геометрии является понятие проекции вектора на прямую или на ось (ось – направленная прямая, причем заданное направление оси называется положительным, а противоположное ему – отрицательным).
Проекцией точки А на ось L называется точка А', в которой пересекаются прямая L и плоскость, перпендикулярная L и проходящая через точку А.
Другими словами, проекцией точки А на ось является основание перпендикуляра АА', опущенного из точки А на эту ось (рис. 1.4).
П
роекцией
вектора
на ось L,
обозначаемой
,
называется вектор
,
где А'
и В'
– проекции начала и конца вектора
Проекция вектора на ось лежит на этой оси и направлена либо вдоль этой оси, либо в противоположном направлении.
Если вектор перпендикулярен оси, то его проекцией на эту ось является нулевой вектор.
Числовой
проекцией вектора на ось L,
обозначаемую
,
называется произведение длины вектора
на косинус угла между вектором
и направлением оси:
.
Частные случаи:
1.
Если
=
или
,
то
= 0;
2.
Если
,
а
,
то
> 0;
3.
Если
,
а
,
то
< 0.
Выполняется следующее равенство:
где – единичный вектор в направлении оси L.
Проекции обладают следующими свойствами:
1.
2.
Пример.
Даны вектор
,
образующий с осью L угол 450,
и вектор
,
образующий с этой же осью угол 1200.
Известно, что
Найти числовую проекцию на ось L вектора
Решение.
Пример.
При каком условии вектор
будет коллинеарен вектору
?
Решение.
Запишем условие коллинеарности векторов
и
:
Тогда:
т. е. для удовлетворения условия задачи необходимо, чтобы векторы и были коллинеарными.