
- •Тема лекции: Аналитическая геометрия (3 часа) Аналитическая геометрия.
- •3.1 Прямая на плоскости
- •Уравнение прямой с угловым коэффициентом.
- •Теорема о нормальном векторе прямой. Вектор с координатами является нормальным для прямой с уравнением на плоскости .
- •3.2. Плоскость в пространстве
- •§ 3.3. Прямая в пространстве
- •Контрольные вопросы:
- •Литературы:
- •Тема лекции: Кривые второго порядка на плоскости. Поверхности второго порядка. (1 час)
- •Контрольные вопросы:
- •Литературы:
Контрольные вопросы:
1. Геометрический смысл углового коэффициента в уравнении прямой на плоскости
2. Уравнение прямой в отрезках.
3. Расстояние от точки до прямой.
4. Условие параллельности двух прямых на плоскости.
5. Условие перпендикулярности прямых на плоскости
6. Условие параллельности плоскостей
7. Условие перпендикулярностей плоскостей
8. Угол между плоскостью и прямой
Литературы:
Основные [1] § 8,9, стр. 49-71
[19] 1.5, стр. 23-33
Дополнительная
[29] Глава 2.6.6. стр. 199-206
Тема лекции: Кривые второго порядка на плоскости. Поверхности второго порядка. (1 час)
Эллипс
Рассмотрим в начале частные виды кривых, определяемых на плоскости уравнениями, в которых неизвестные и присутствуют только в первой или во второй степени.
1.
Пусть на плоскости
имеются две точки
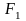 и
и
 ,
называемые фокусами
на расстоянии
,
называемые фокусами
на расстоянии
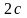 друг от друга (
– фокусное расстояние). Для определенности
расположим их на оси
симметрично относительно начало
координат, т.е.
друг от друга (
– фокусное расстояние). Для определенности
расположим их на оси
симметрично относительно начало
координат, т.е.
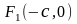 и
и
 .
.
Пусть 2a>2c
Определение.
Эллипсом
называется геометрическое место точек
плоскости, сумма расстояний, от которых
до двух выбранных фокусов, постоянна и
равна
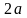 (см. рис. 4.1).
(см. рис. 4.1).
Из
условия
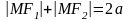 выведем уравнение эллипса, положив
,
получим
выведем уравнение эллипса, положив
,
получим
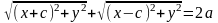 ;
;

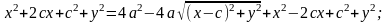
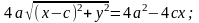

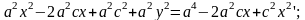
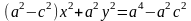 .
.
Поскольку
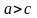 ,
то
,
то
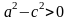 .
Обозначив
.
Обозначив
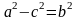 ,
получим
,
получим
 ,
,
 .
.
Разделив
части уравнения на
 ,
получим:
,
получим:
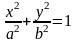 ,
где
,
где
 .
.
Это уравнение называется каноническим уравнением эллипса, а числа а и его полуосями (большой и малой).
 D1 Y
D2
D1 Y
D2
M
 O
X
F1
F2
O
X
F1
F2
Рис. 4.1
Подставив
в каноническое уравнение значение
,
получим
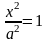 ;
;
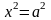 ,
,
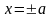 ,
т.е. эллипс пересекает ось
в точках с координатами
.
Аналогично проверяется, что ось
эллипс пересекает в точках
,
т.е. эллипс пересекает ось
в точках с координатами
.
Аналогично проверяется, что ось
эллипс пересекает в точках
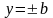 .
Эти точки пересечения эллипса с осями
координат называются вершинами
эллипса.
.
Эти точки пересечения эллипса с осями
координат называются вершинами
эллипса.
Несложно
проверить, что т.
является центром симметрии эллипса,
описываемого каноническим уравнением,
а оси
и
его осями симметрии. Ось, проходящая
через фокусы эллипса (ось
),
называется его фокальной
осью. Число
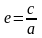 называется эксцентриситетом.
У эллипса
называется эксцентриситетом.
У эллипса
 .
.
Прямые,
проходящие перпендикулярно фокальной
оси на расстоянии
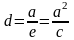 от центра эллипса, называются директрисами
эллипса
(на рис. 2.13
обозначены через
от центра эллипса, называются директрисами
эллипса
(на рис. 2.13
обозначены через
 и
и
 ).
).
Пример
1. Найдем
каноническое уравнение, фокусы полуоси,
эксцентриситет и директрисы эллипса
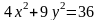 .
.
Разделив обе части уравнения на 36, получим:
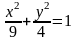 .
.
Поскольку
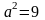 ,
,
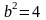 то полуоси равны
то полуоси равны
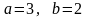 .
Из соотношения
.
Из соотношения
 получим, что
получим, что
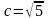 и фокусы эллипса находятся в точках
и фокусы эллипса находятся в точках
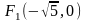 ,
,
 .
Эксцентриситет равен
.
Эксцентриситет равен
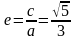 ,
а директрисы имеют уравнение
,
а директрисы имеют уравнение
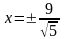 .
.
Замечание 1. Уравнение
,
где

определяет
эллипс с полуосями
и а, фокусы которого находятся на оси
в точках
 ,
,
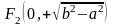 .
.
Его эксцентриситет равен
 ,
,
а
директрисы перпендикулярны оси
и находятся на расстоянии
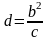 от начала координат (см. рис. 4.2).
от начала координат (см. рис. 4.2).
 Y
Y
 D2
D2
F2
X
F1

D1
Рис.4.2
Замечание 2. Уравнение

определяет
эллипс, полученный из эллипса с
каноническим уравнением путем
параллельного переноса его центра в
точку
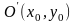 .
При этом параллельно переносится сам
эллипс, его фокусы и директрисы. Это
следует из того, что при замене переменных
.
При этом параллельно переносится сам
эллипс, его фокусы и директрисы. Это
следует из того, что при замене переменных
 и
и
 система координат
система координат
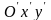 получается из
путем параллельного переноса точки
в точку
получается из
путем параллельного переноса точки
в точку
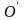 .
.
Пример
2. Нарисуем
эллипс с уравнением
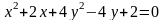 .
.
Найдем его центр, полуоси, фокусы и директрисы.
Для этого выделим полные квадраты для неизвестных и , получим
 ;
;
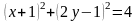 ;
;
 ;
;
 .
.
Этот
эллипс имеет центр в точке
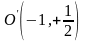 ,
полуоси
,
полуоси
 .
Поскольку
.
Поскольку
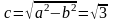 ,
то его фокусы находятся в точках
,
то его фокусы находятся в точках
 и
и
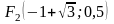 ,
а поскольку
,
а поскольку
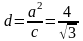 ,
то директрисы имеют уравнения
,
то директрисы имеют уравнения
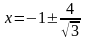 (см. рис. 4.3).
(см. рис. 4.3).
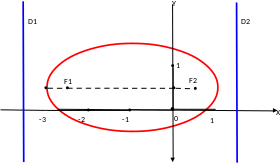
Рис. 4.3
2.
В частном случае, когда фокусное
расстояние эллипса
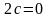 ,
два фокуса эллипса совпадают с его
центром. При этом
,
два фокуса эллипса совпадают с его
центром. При этом
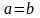 и каноническое управление эллипса
принимает вид
и каноническое управление эллипса
принимает вид
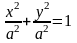 или
или
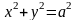 .
.
Это
уравнение называется каноническим
уравнением окружности
радиуса а. У
окружности эксцентриситет
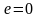 ,
а директрисы отсутствуют.
,
а директрисы отсутствуют.
Уравнение окружности радиуса а с центром в точке имеет вид:
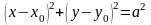 .
.
Пример3.
Запишем уравнение окружности с центром
в точке
 ,
проходящей через начало координат.
Поскольку радиус окружности
,
проходящей через начало координат.
Поскольку радиус окружности
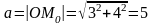 ,
то уравнение этой окружности имеет вид
,
то уравнение этой окружности имеет вид
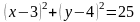 .
.

Рис. 4.4
Эллипсы (в частности окружности) широко встречаются в природе и технике. Например, планеты вращаются вокруг солнца по эллипсам, в одном из фокусов которых находится солнце.
Гипербола
Пусть
на плоскости имеются два фокуса (например
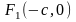 и
и
 и
пусть
и
пусть
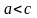 .
.
Определение.
Гиперболой
называется геометрическое место точек
плоскости, разность расстояний от
которых до двух выбранных фокусов
постоянна и равна
 .
.
И каноническим уравнением гиперболы записывается так:
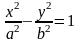 ,
где
,
где
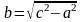 .
.
Число а называется действительной полуосью гиперболы, а число – ее мнимой полуосью.
Подставив
в каноническое уравнение
,
получим
,
т.е.
,
следовательно, гипербола пересекает
ось
в точках
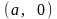 и
и
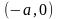 .
Эти точки называются вершинами
гиперболы.
Подставив в каноническое уравнение
.
Эти точки называются вершинами
гиперболы.
Подставив в каноническое уравнение
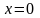 ,
получим
,
получим
 .
Это уравнений решения не имеет, поэтому
гипербола с каноническим уравнением с
осью
не пересекается.
.
Это уравнений решения не имеет, поэтому
гипербола с каноническим уравнением с
осью
не пересекается.
Как и у эллипса, т. является центром симметрии гиперболы, а оси и ее осями симметрии.
Определения
эксцентриситета
и директрис
гиперболы повторяют соответствующие
определения для эллипса. Эксцентриситет
гиперболы
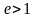 .
.
Определение.
Прямая
называется асимптотой
кривой
 ,
если расстояние от точки на кривой до
этой прямой стремится к нулю при удалении
точки вдоль кривой в бесконечность.
,
если расстояние от точки на кривой до
этой прямой стремится к нулю при удалении
точки вдоль кривой в бесконечность.
Это определение не вполне корректно. Точное определение асимптоты опирается на понятие предела, которое будет изучаться позже. В четвертом модуле будет приведено доказательство следующего факта.
Прямые
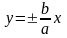 являются асимптотами обеих ветвей
гиперболы
являются асимптотами обеих ветвей
гиперболы
.
Гипербола изображена на рис. 4.5.

Рис 4.5
Пример
1. Найти
каноническое уравнение, полуоси, фокусы,
эксцентриситет, директрисы и асимптоты
гиперболы
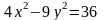 .
.
Разделив обе части уравнения на 36, получим:
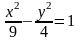 .
.
Следовательно,
действительная полуось
 ,
мнимая
,
мнимая
 .
Из соотношения
.
Из соотношения
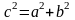 получим, что
получим, что
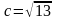 и фокусы гиперболы находятся в точках
и фокусы гиперболы находятся в точках
 .
.
Эксцентриситет
равен
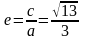 ,
а директрисы имеют уравнения
,
а директрисы имеют уравнения
 . Уравнения
асимптот:
. Уравнения
асимптот:
 .
.
Замечание 1. Уравнение
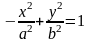
определяет гиперболу с действительной полуосью и мнимой полуосью , фокусы которой находятся на оси в точках:
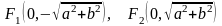
Ее
эксцентриситет равен
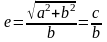 ,
,
а директрисы перпендикулярны оси и находятся на расстоянии от начала координат. Уравнения асимптот имеют тот же вид: . Сопряженная гипербола изображена на рис.4.6.
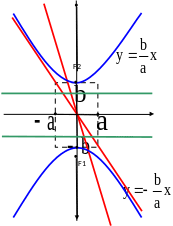
Рис. 4.6
Гиперболы и называются сопряженными друг другу.
Замечание 2. Уравнение
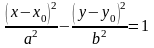
определяют гиперболу, полученную из гиперболы путем параллельного переноса. Центр гиперболы находится в точке .
Пример.
Изобразим
гиперболу
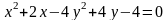 .
Найдем ее центр, полуоси, фокусы,
директрисы и асимптоты.
.
Найдем ее центр, полуоси, фокусы,
директрисы и асимптоты.
Выделив полные квадраты, получим:

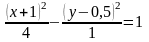
Эта
гипербола имеет центр в точке
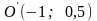 ,
действительную полуось
,
действительную полуось
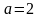 и мнимую полуось
и мнимую полуось
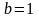 .
.
Поскольку
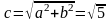 ,
то ее фокусы находятся в точках
,
то ее фокусы находятся в точках
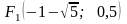 и
и
 ,
и поскольку
,
и поскольку
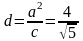 ,
,
то директрисы имеют уравнения
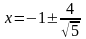 .
.
Угловые
коэффициенты асимптот, проходящих через
точку
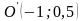 ,
равны
,
равны
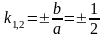 .
.
Поэтому уравнения этих асимптот имеют вид (см. рис. 2.19)
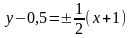 .
.
Пример. Космическое тело, пролетающее, через солнечную систему движется по траектории в форме гиперболы, в фокусе которой находятся солнце.
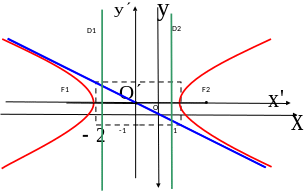
Рис. 4.7
Парабола.
Пусть
на плоскости имеется прямая
(директриса)
и точка
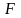 (фокус)
на расстоянии
от директрисы. Пусть
имеет уравнение
(фокус)
на расстоянии
от директрисы. Пусть
имеет уравнение
 ,
фокус - координаты
,
фокус - координаты
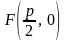 .
.
Определение. Параболой называется геометрическое место точек плоскости, расстояние от которых до фокуса совпадает с расстоянием до директрисы (см. рис. 2.19).
Пусть
-
проекция точки
на директрису
.
Из условия
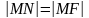 выведем уравнение параболы:
выведем уравнение параболы:
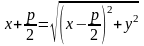
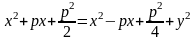
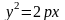 .
.
Это
уравнение называется каноническим
уравнением
параболы, а
число
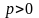 ее параметром.
ее параметром.
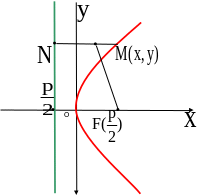
Рис. 4.8
Парабола
проходит через точкой
,
которая называется ее вершиной.
Ось
является осью симметрии параболы.
Эксцентриситет
 параболы всегда считается равным
единице. Асимптот у параболы нет.
параболы всегда считается равным
единице. Асимптот у параболы нет.
Замечание 1. Пусть
а)
Уравнение
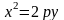 определяет параболу с фокусом
определяет параболу с фокусом
 и директрисой
и директрисой
 (см. рис. 4.9);
(см. рис. 4.9);
в)
Уравнение
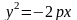 определяет параболу с фокусом
определяет параболу с фокусом
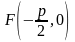 и директрисой
и директрисой
 (см. рис. 4.10);
(см. рис. 4.10);
с)
Уравнение
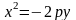 определяет параболу с фокусом
определяет параболу с фокусом
 и директрисой
и директрисой
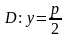 (см. рис. 4.11);
(см. рис. 4.11);
Во всех отмеченных случаях вершина параболы находится в начале координат.
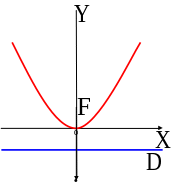 Рис.
4.9
Рис.
4.9
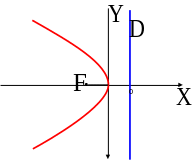
Рис.4.10

Рис. 4.11
Пример
1. Найдем
параметр, фокус и директрису параболы
 . Поскольку
. Поскольку
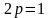 ,
то
,
то
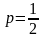 .
В соответствии с пунктом а) замечания
1 фокус параболы находится в точке
.
В соответствии с пунктом а) замечания
1 фокус параболы находится в точке
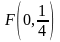 ,
а уравнение директрисы есть
,
а уравнение директрисы есть
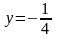 .
.
Замечание
2. Уравнение

определяет параболу с вершиной в точке , полученную путем параллельного переноса параболы . Подобные уравнения:
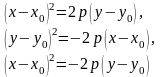
определяют параболы с вершинами в точке , направление ветвей, которых соответствует соответствующему направлению ветвей парабол из замечания 1.
Пример 2. Найдем вершину, параметр, фокус и директрису параболы
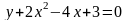 .
.
Выделив полный квадрат по переменной х, получим:
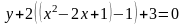 ;
;
 ;
;
 .
.
Поэтому
вершина параболы имеет координаты
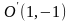 ,
параметр
,
параметр
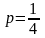 и ветви параболы направлены вниз (случай
с). Фокус параболы смещен на величину
и ветви параболы направлены вниз (случай
с). Фокус параболы смещен на величину
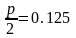 ниже вершины и имеет координаты
ниже вершины и имеет координаты
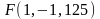 ,
ее директриса расположена выше вершины
и имеет уравнения
,
ее директриса расположена выше вершины
и имеет уравнения
 (рис. 4.12)
(рис. 4.12)
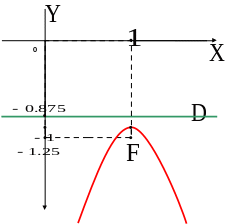
Рис. 4.12
Пример 3. Тело, брошенное под углом к горизонту вблизи поверхности земли, при отсутствии сопротивление воздуха движется по траектории, имеющей форму параболы, направленной ветвями вниз.
Приведем без доказательства следующую теорему, дающую единый подход к определению эллипса, гиперболы и параболы.

Рис. 4.13
Теорема.
Пусть на
плоскости заданы прямая
(директриса) и точка
(фокус), не лежащая на
.
Пусть задано число
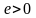 (эксцентриситет). Тогда геометрическое
место точек
плоскости таких, что отношение расстояние
от
до
к расстоянию от
до
равно
,
является:
(эксцентриситет). Тогда геометрическое
место точек
плоскости таких, что отношение расстояние
от
до
к расстоянию от
до
равно
,
является:
а)
эллипсом, при
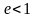 ;
;
в) гиперболой, при ;
с)
параболой, при
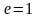 .
.
(см. рис. 4.13)
Общее уравнение кривой второго порядка
Определение. Кривой второго порядка называется множество точек плоскости, декартовы координаты которых удовлетворяют уравнению
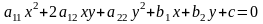 .
.
Здесь
хотя бы одно из чисел
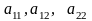 отлично от нуля. Это уравнение называется
общим
уравнением кривой второго порядка.
отлично от нуля. Это уравнение называется
общим
уравнением кривой второго порядка.
Если на плоскости должным образом выбрать систему координат , то в этой системе координат уравнение кривой примет канонический вид одной из кривых, рассмотренных выше (кроме нескольких вырожденных случаев).
Теорема.
Для любой
кривой второго порядка найдется декартова
система координат
,
в которой уравнение кривой примет один
из следующих видов. (Здесь
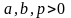 ).
).
1) - (эллипс);
2) - (гипербола);
3) - (парабола);
4)
 -
(точка
);
-
(точка
);
5)
 или
или 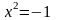 (пустые множества);
(пустые множества);
6)
 (пара пересекающихся прямых)
(пара пересекающихся прямых)
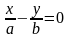 и
и
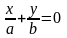 .
.
7) (пара параллельных прямых ).
8)
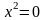 (прямая – ось
).
(прямая – ось
).
Поверхности второго порядка
Рассмотрим вначале частные виды поверхностей, определяемых в пространстве уравнениями, в которых неизвестные присутствуют только в первой или во второй степени.
Пусть в пространстве имеется кривая и прямая .
Определение. Цилиндрической поверхностью (цилиндром) с направляющей и образующей называется геометрическое место точек пространства, лежащих на прямых, проходящих через точки параллельно
(см. рис. 4.14).

Рис. 4.14
Замечание.
Если кривая
находится на плоскости
и имеет уравнение
 ,
то это же уравнение определяет в
пространстве
цилиндрическую поверхность с направляющей
и образующей
.
В самом деле, если
,
то это же уравнение определяет в
пространстве
цилиндрическую поверхность с направляющей
и образующей
.
В самом деле, если
 (т.е. если
(т.е. если
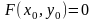 ),
то прямая, проходящая
через
параллельно
,
имеет параметрические уравнения:
),
то прямая, проходящая
через
параллельно
,
имеет параметрические уравнения:

Очевидно,
что любая точка этой прямой удовлетворяет
уравнению
.
Кроме того, если точка
 не лежит на прямой вида
,
то точка
не принадлежит
,
т. к.
не лежит на прямой вида
,
то точка
не принадлежит
,
т. к.
 .
.
Из
этого замечания следует, что уравнение
любой кривой
второго порядка на плоскости
определяет в пространстве
одну из восьми цилиндрических поверхностей
с образующей
.
Перечислим эти поверхности и их
канонические уравнения.
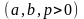 .
.
Эллиптический цилиндр имеет направляющей эллипс и каноническое уравнение

(см. рис. 4.15.)
Рис. 4.15
В частности, круговой цилиндр: имеет направляющей окружность.
1.2 Гиперболический цилиндр имеет направляющей гиперболу и каноническое уравнение
(см. рис. 2.27)
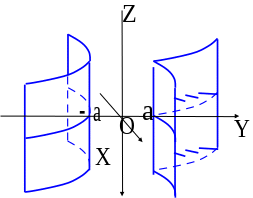
Рис. 4.16
1.3. Параболический цилиндр имеет направляющей параболу и каноническое уравнение
( см.
рис. 4.17)
см.
рис. 4.17)
Рис. 4.17
1.4. Уравнение определяет ось
1.5. Уравнения и - пустое множество.
1.6. Уравнение - пара пересекающихся по оси плоскостей
1.7. - пара плоскостей, параллельных .
1.8. - плоскость .
Все перечисленные поверхности называются цилиндрическими поверхностями второго порядка.
Пусть в пространстве имеется кривая и точка , не лежащая на .
Определение. Конической поверхностью (конусом) с направляющей и вершиной называется геометрическое место точек пространства, лежащих на прямых, проходящих через и пересекающих .
В частности, конические поверхности, рассматриваемые в школьной программе, имели направляющие окружности , их вершины находились на прямой, проходящей через центр перпендикулярно плоскости окружности.
Заметим, что вершина любой конической поверхности является ее центром симметрии.
Уравнение
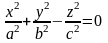

называется
каноническим
уравнением конуса второго порядка.
Проверим, что это уравнение на самом
деле определяет коническую поверхность
с вершиной
и направляющей – эллипсом, лежащим в
плоскости
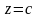 .
.
Что бы найти линию, лежащую в пересечении конуса второго порядка и плоскости , достаточно решить систему из этих двух уравнений, т.е. подставить в уравнение конуса. Получим:
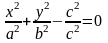
что есть каноническое уравнение эллипса.
Если
точка
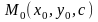 лежит на этом эллипсе, то уравнения
прямой, проходящей через точки
и
,
имеет вид:
лежит на этом эллипсе, то уравнения
прямой, проходящей через точки
и
,
имеет вид:
 .
.
Проверим что, любая точка этой прямой лежит на конусе второго порядка; для этого подставим координаты точек прямой в уравнение конуса, получим:
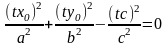 ;
;
 ;
если
;
если
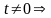
 ,
,
что верно, поскольку удовлетворяет уравнению эллипса.
Заметим,
что сечение этого конуса любой плоскостью
 или
,
проходящей через ось конуса
дает пару пересекающихся прямых:
или
,
проходящей через ось конуса
дает пару пересекающихся прямых:
 ;
;
 .
.
Поэтому других точек, кроме как лежащих на прямых вида поверхность не имеет (см. рис. 4.18).
Проверьте,
что координатные плоскости
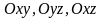 являются плоскостями симметрии, а оси
осями симметрии этого конуса.
являются плоскостями симметрии, а оси
осями симметрии этого конуса.
В случае сечение конуса плоскостью дает окружность .
Поэтому в этом случае конус является поверхностью вращения, которая получается в результате вращения пары прямых
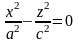 ,
лежащих в плоскости
вокруг оси
.
,
лежащих в плоскости
вокруг оси
.

Рис.4.18
При пересечении конической поверхности второго порядка различными плоскостями линиями пересечения могут оказаться только эллипс, гипербола, парабола, точка, прямая или пара пересекающихся прямых. Поэтому раньше кривые второго порядка называли коническими сечениями.
Поверхность, определяемая каноническими уравнениями
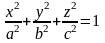
называется
эллипсоидом,
а числа
 – его полуосями.
– его полуосями.
Выясним форму эллипсоида с помощью метода сечений, который состоит в следующем. Находятся линии, лежащие в пересечении исследуемой поверхности различными плоскостями. Эти линии, построенные затем в системе координат и определяют форму поверхности.
Найдем линии пересечения эллипсоида с координатными плоскостями.
а)
С плоскостью
.
Подставив
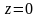 из уравнения этой плоскости в уравнение
эллипсоида, получим
из уравнения этой плоскости в уравнение
эллипсоида, получим
,
что есть уравнения эллипса с полуосями a и в плоскости .
в) С плоскостью .
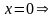
 .
.
Это уравнение эллипса с полуосями и c в плоскости .
с) С плоскостью .

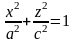 ,
,
что задает эллипс с полуосями a и c в плоскости .
При желании можно рассмотреть и другие плоскости. Во всех случаях в сечениях получаются эллипсы, точки или пустые множества. Следовательно, эллипсоид имеет следующий вид (см. рис. 4.19).
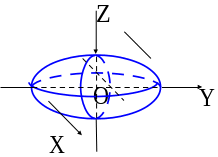 рис.
4.19
рис.
4.19
Этот эллипсоид симметричен относительно т. , координатных осей и координатных плоскостей.
Эллипсоиды используются в различных технических науках. Например, деформации абсолютно упругого тела в данной точке по различным направлениям имеют величины, определяемые так называемым эллипсоидом деформаций.
В
случае равенства двух полуосей, например,
,
сечения эллипсоида любой плоскостью
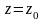 ,
где
,
где
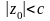 дают окружности. Поэтому такой эллипсоид
дают окружности. Поэтому такой эллипсоид
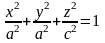
получается в результате вращения эллипса
,
лежащего в плоскости вокруг оси .
В
случае равенства трех полуосей
 эллипсоид превращается в сферу радиуса
с центром в начале координат.
эллипсоид превращается в сферу радиуса
с центром в начале координат.
Ее
уравнение:
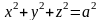 .
.
Поверхность, определяемая каноническим уравнением
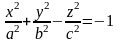 (a,
b,
c>0),
(a,
b,
c>0),
называется двуполостным гиперболоидом.
Выясним ее форму с помощью метода сечений.
а) При получаем
,
что определяет пустое множество. Следовательно, с плоскостью этот гиперболоид не пересекается.
в) При получаем
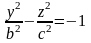 .
.
Это гипербола, лежащая в плоскости , с действительной полуосью с и мнимой полуосью , ветви которой направлены вдоль оси .
с) При получим
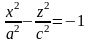 .
.
Это
гипербола, лежащая в плоскости,
с действительной полуосью с мнимой
полуосью
,
ветви которой направлены вдоль оси
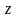 .
.
Следовательно,
двуполостный гиперболоид имеет следующий
вид поверхности, состоящей из двух
частей (см. рис. 4.20), симметричной
относительно т.
,
,
 и
.
и
.
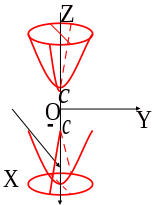
Рис.4.20
При
сечения гиперболоида плоскостью
,
где
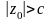 определяют окружности, по этому
гиперболоид
определяют окружности, по этому
гиперболоид

получается в результате вращения гиперболы
,
лежащей в плоскости вокруг .
Поверхность, определяемая каноническим уравнением
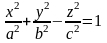 ,
,
,
,
называется однополостным гиперболоидом..
Определим ее форму с помощью метода сечений.
а) При получаем уравнение
,
которое определяет эллипс с полуосями a и b, лежащего в плоскости .
в) При получаем
 .
.
Это гипербола, лежащая в плоскости , с действительной полуосью и мнимой полуосью c, ветви которой направлены вдоль оси .
с) При y=0 получаем уравнение гиперболы, лежащей в плоскости с действительной полуосью a и мнимой c:
 .
.
Поэтому однополостный гиперболоид имеет следующий вид (см. рис. 4.21).

Рис. 4.21.
Эта
поверхность симметрична относительно
т.
,
,
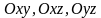 .
.
При однополостный гиперболоид

получается в результате вращения гиперболы , лежащей в плоскости вокруг оси .
Двуполостный
гиперболоид обладает одним замечательным
свойством. Сечение гиперболоида любой
касательной к нему плоскостью состоит
из двух пересекающихся в точке касания
прямых. Например, сечение гиперболоида
плоскостью
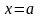 дает:
дает:
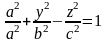 ;
;
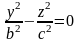 .
.
Это
уравнение определяет две пересекающиеся
в точке
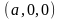 прямые в плоскости
.
прямые в плоскости
.
Поэтому поверхность, имеющую форму однополостного гиперболоида можно целиком составить из прямых линий. Строительные конструкции такой формы обладают большой прочностью при относительной простоте изготовления. Так первая телебашня в г. Москве составлена из кусков гиперболоидов, каждый из которых построен из прямолинейных металлических форм (см. рис. 4.22).

Рис. 4.22
6) Поверхность, определяемая каноническим уравнением
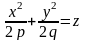
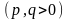 ,
,
называется эллиптическим параболоидом. Определим его форму.
а) При получим
 .
.
Это
точка
 .
Следовательно, параболоид пересекает
(касается) плоскость
в точке
.
.
Следовательно, параболоид пересекает
(касается) плоскость
в точке
.
в) При получаем
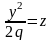
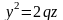 .
.
Это
уравнение параболы в плоскости
с параметром
 ,
ветви которой направлены в сторону
положительной полуоси
.
,
ветви которой направлены в сторону
положительной полуоси
.
с) При получаем

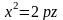 .
.
Это уравнение параболы в плоскости с параметром , ветви которой направлены в сторону положительной полуоси .
Поэтому эллиптический параболоид имеет следующий вид (см. рис. 4.23).

Рис. 4.23
Плоскости
и
являются его плоскостями симметрии, а
ось
- осью симметрии. При
 эллиптический параболоид получается
в результате вращения параболы
,
лежащей в плоскости
вокруг оси
.
У такого параболоида вращения все
параболы, лежащие в пересечении
плоскостей, проходящих через ось
с параболоидом имеют общий фокус –
точку
эллиптический параболоид получается
в результате вращения параболы
,
лежащей в плоскости
вокруг оси
.
У такого параболоида вращения все
параболы, лежащие в пересечении
плоскостей, проходящих через ось
с параболоидом имеют общий фокус –
точку
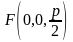 .
Параболоид вращения обладает следующим
свойством. Если в точку
поместить точечный источник света, то
после отражения от параболоида поток
света становится параллельным оси
.
Поэтому светоотражатели во всех фарах,
фонарях и прожекторах делают в форме
параболоидов вращения.
.
Параболоид вращения обладает следующим
свойством. Если в точку
поместить точечный источник света, то
после отражения от параболоида поток
света становится параллельным оси
.
Поэтому светоотражатели во всех фарах,
фонарях и прожекторах делают в форме
параболоидов вращения.
Параллельный поток света, направленный вдоль оси параболоида вращения после отражения от него собирается в фокусе парабол – точке . Поэтому зеркала телескопов – рефлекторов также имеют форму параболоида вращения, в фокусе которого ставится дополнительное зеркало, выводящее поток света в окуляр телескопа. Форму параболоида вращения имеют также все параболические антенны и локаторы.
7. Поверхность, определяемая каноническим уравнением
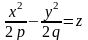 ,
,
называется гиперболическим параболоидом.
а) При получаем
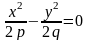 .
.
Это уравнение двух пересекающихся прямых в плоскости .
б) При получаем
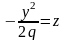 ;
;
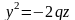 .
.
Это уравнение параболы в плоскости , ветви которой направлены вдоль отрицательной полуоси .
с) При получаем уравнение параболы в плоскости , ветви которой направлены вдоль положительной полуоси .
Поверхность такой формы называется седловой поверхностью (см. рис. 4.24).

Рис. 4.24
У этой поверхности и - плоскости симметрии, ось - ось симметрии.
Так же, как и однополостный гиперболоид, эллиптический параболоид можно составить из прямых линий. С помощью конструкций в виде гиперболического параболоида, составленных из прямолинейных балок осуществляют строительство перекрытий больших размеров, например, крыш над стадионами.
8. Определение. Поверхностью второго порядка называется множество точек пространства, декартовы координаты которых удовлетворяют уравнению
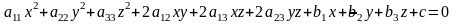
Здесь
хотя бы один коэффициент
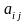 должен быть отличен от нуля.
должен быть отличен от нуля.
Заметим, что все рассмотренные выше поверхности подходят под это определение. Оказывается, что этими поверхностями и исчерпываются поверхности второго порядка.
Теорема. Любая поверхность второго порядка в пространстве является одной из следующих поверхностей:
одной из цилиндрических поверхностей второго порядка;.
конусом второго порядка;.
Эллисоидом
одно – или двуполостным гиперболоидом;
эллиптическим или гиперболическим параболоидом.
Найдется,
такая декартова система координат
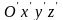 ,
в которой уравнение поверхности принимает
канонический вид.
,
в которой уравнение поверхности принимает
канонический вид.
Без доказательства.
Определение
вида поверхности и получение канонического
уравнения из общего является довольно
сложной процедурой, но в случае отсутствия
в уравнении членов с произведениями
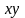 ,
,
 и
и
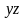 приведение общего уравнения к каноническому
достигается (как и для кривых второго
порядка) методом выделения полных
квадратов и параллельным переносом
осей координат.
приведение общего уравнения к каноническому
достигается (как и для кривых второго
порядка) методом выделения полных
квадратов и параллельным переносом
осей координат.
Пример. Выясним тип, расположение и канонический вид уравнения поверхности второго порядка, заданной уравнением
 .
.
Преобразуем уравнение, выделив полные квадраты для переменных :
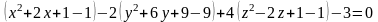 ;
;
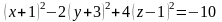 ;
;
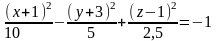
При
параллельном переносе системы координат,
задаваемом формулами
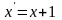 ,
,
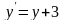 ,
,
 начало новой системы координат
окажется в точке
начало новой системы координат
окажется в точке
 ,
а уравнение поверхности примет
канонический вид
,
а уравнение поверхности примет
канонический вид
 .
.
Следовательно,
данная поверхность – двуполостный
гиперболоид с центром в точке
и с осью
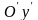 .
.
