
- •Тема лекции: Аналитическая геометрия (3 часа) Аналитическая геометрия.
- •3.1 Прямая на плоскости
- •Уравнение прямой с угловым коэффициентом.
- •Теорема о нормальном векторе прямой. Вектор с координатами является нормальным для прямой с уравнением на плоскости .
- •3.2. Плоскость в пространстве
- •§ 3.3. Прямая в пространстве
- •Контрольные вопросы:
- •Литературы:
- •Тема лекции: Кривые второго порядка на плоскости. Поверхности второго порядка. (1 час)
- •Контрольные вопросы:
- •Литературы:
§ 3.3. Прямая в пространстве
Пусть
в пространстве
имеется прямая
с направляющим вектором
 .
– фиксированная точка этой прямой,
.
– фиксированная точка этой прямой,
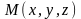 – произвольная точка на
.
– произвольная точка на
.
1. Запись векторного уравнения прямой

ничем не отличается от записи векторного уравнения прямой на плоскости (рис.3.12).

2. Записав три координаты обеих частей векторного уравнения прямой, получим

Эти уравнения называются параметрическими уравнениями прямой в пространстве.
3.
Поскольку векторы
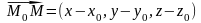 и
коллинеарны, то их координаты
пропорциональны, поэтому
и
коллинеарны, то их координаты
пропорциональны, поэтому
 .
.
Эти
уравнения называются каноническими
уравнениями прямой в пространстве.
В соответствии с количеством знаков
равенства таких уравнений два
 и понимать их нужно в смысле пропорций.
и понимать их нужно в смысле пропорций.
Из-за того, что в знаменателях канонических уравнений могут оказаться нули, предпочтительнее пользоваться параметрическими уравнениями.
Пример
1. Запишем
уравнения прямой
,
проходящей через точки
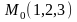 и
и
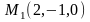 .
.
Направляющий
вектор этой прямой
имеет координаты
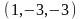 .
Поэтому параметрические уравнения этой
прямой записывается в виде:
.
Поэтому параметрические уравнения этой
прямой записывается в виде:
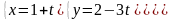
а канонические уравнения:
 .
.
Пример
2. Запишем
уравнений прямой
,
проходящей через точку
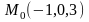 перпендикулярно плоскости
перпендикулярно плоскости
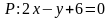 .
.
Нормальный
вектор плоскости есть
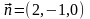 .
Этот же вектор параллелен прямой
,
поэтому его можно взять в качестве
направляющего вектора. Подставив
координаты в уравнение, получим уравнения
.
Этот же вектор параллелен прямой
,
поэтому его можно взять в качестве
направляющего вектора. Подставив
координаты в уравнение, получим уравнения
 и
и
 .
.
Заметим, что поскольку направляющий вектор параллелен плоскости , то эта прямая перпендикулярна .
Теорема 1. Косинус угла между прямыми
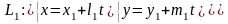 и
и 
находится по формуле
 .
.
Эти прямые перпендикулярны только в том случае, когда
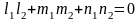 .
.
Эти прямые параллельны только в том случае, когда
 .
.
Если при выполнении этого условия
 ,
,
то прямые и совпадают. Все утверждения этой теоремы следуют из соответствующих свойств направляющих векторов. В последнем случае прямые и имеют общую точку.
Пример 3. Найдем косинус угла между прямыми
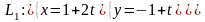 и
и
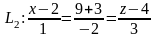 .
.
Поскольку
направляющие векторы этих прямых есть
 и
и
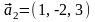 ,
то
,
то
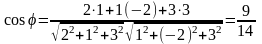 .
.
Теорема 2. Синус угла между плоскостью и прямой

находится по формуле:
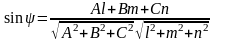 .
.
Прямая и плоскость перпендикулярны только в том случае, когда
 .
.
Прямая параллельна плоскости только в том случае, когда
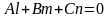 .
.
Если при выполнении этого условия
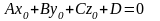 ,
,
то прямая лежит в плоскости .
Доказательство
этой теоремы следует из того, что угол
между прямой и плоскостью
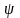 в сумме с углом
в сумме с углом
 составляют
составляют
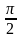 .
Здесь
– направляющий вектор прямой, а
–
нормальный вектор плоскости (см. рис.
3.13).
.
Здесь
– направляющий вектор прямой, а
–
нормальный вектор плоскости (см. рис.
3.13).
0
L
Рис. 3.13
Поэтому
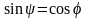 ;
;
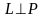 только в том случае, когда
||
;
||
только в том случае, когда
только в том случае, когда
||
;
||
только в том случае, когда
 .
.
Пример 4. Найдем синус угла между прямой

и
плоскостью  и точку их пересечения.
и точку их пересечения.
Поскольку
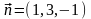 и
и
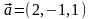 ,
то
,
то
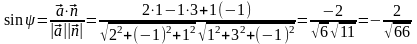 .
.
Для
того, чтобы найти точку пересечения
прямой и плоскости, решим систему из
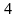 –х
уравнений с 4–мя неизвестными, составленную
из уравнения плоскости и трех
параметрических уравнений прямой:
–х
уравнений с 4–мя неизвестными, составленную
из уравнения плоскости и трех
параметрических уравнений прямой:
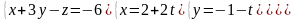 .
.
Подставив три последних уравнения в первое, получим
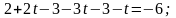
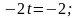
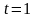 .
.
Отсюда
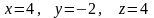 .
Эти числа и составляют координаты точки
пересечения
.
Эти числа и составляют координаты точки
пересечения
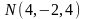 .
.
4. Две параллельные плоскости в пересечении определяют прямую в пространстве. Система из двух уравнений этих плоскостей с тремя неизвестными называется общими уравнениями прямой:
 .
.
Чтобы из общих уравнений прямой получить ее канонические или параметрические уравнения можно поступать двумя способами.
а)
Найти направляющий вектор прямой в виде
векторного произведения
 ,
где
,
где
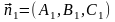 и
и
 –
нормальные вектора плоскостей, т.к.
вектор
перпендикулярен
и
.
Затем найти какое-либо решение системы
уравнений – координаты точки на этой
прямой и подставить координаты
направляющего вектора и точки в
соответствующие уравнения.
–
нормальные вектора плоскостей, т.к.
вектор
перпендикулярен
и
.
Затем найти какое-либо решение системы
уравнений – координаты точки на этой
прямой и подставить координаты
направляющего вектора и точки в
соответствующие уравнения.
б)
Более короткий способ – это решение
системы общих уравнений методом Гаусса.
Поскольку плоскости не параллельны, то
 ,
отсюда следует, что ранг матрицы системы
равен 2, а так как количество неизвестных
равно 3, решение системы содержит один
параметр
,
т.е. в результате решения системы сразу
получаются параметрические уравнения
прямой.
,
отсюда следует, что ранг матрицы системы
равен 2, а так как количество неизвестных
равно 3, решение системы содержит один
параметр
,
т.е. в результате решения системы сразу
получаются параметрические уравнения
прямой.
Пример 5. Запишем параметрические и канонические уравнения прямой, заданной общими уравнениями:
 .
.
Составим расширенную матрицу системы и приведем ее к верхнетреугольному виду:
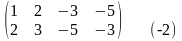
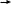 ~
~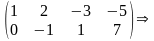
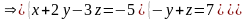 .
.
Эти
уравнения и являются параметрическими
уравнениями прямой. Т.к.
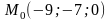 -
точка на прямой и
-
точка на прямой и
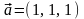 ее направляющий вектор, то канонические
уравнения прямой имеют вид:
ее направляющий вектор, то канонические
уравнения прямой имеют вид:
 .
.
