
- •Тема лекции: Аналитическая геометрия (3 часа) Аналитическая геометрия.
- •3.1 Прямая на плоскости
- •Уравнение прямой с угловым коэффициентом.
- •Теорема о нормальном векторе прямой. Вектор с координатами является нормальным для прямой с уравнением на плоскости .
- •3.2. Плоскость в пространстве
- •§ 3.3. Прямая в пространстве
- •Контрольные вопросы:
- •Литературы:
- •Тема лекции: Кривые второго порядка на плоскости. Поверхности второго порядка. (1 час)
- •Контрольные вопросы:
- •Литературы:
3.2. Плоскость в пространстве
Все уравнения плоскостей в пространстве с небольшими изменениями повторяют уравнения прямой на плоскости, доказательства этих уравнений также аналогичны. Мы предлагаем читателю сравнить пункты этой лекции с соответствующими пунктами предыдущей.
1.
Пусть плоскость
 в пространстве
в пространстве
 пересекает ось
пересекает ось
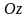 в точке с координатой
,
а угловые коэффициенты ее пересечения
с плоскостями
в точке с координатой
,
а угловые коэффициенты ее пересечения
с плоскостями
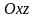 и
и
 равны соответственно
равны соответственно
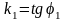 и
и
 (см. рис.2.9).
(см. рис.2.9).
Тогда уравнение этой плоскости имеет вид
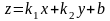 .
.
Это уравнение называется уравнением плоскости с угловыми коэффициентами.
С помощью такого уравнения можно описать любую плоскость , не параллельную . Выводить это уравнение мы не будем.
2.
Определение.
Любые два
неколлинеарных вектора
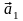 и
и
 на плоскости
называются ее направляющими
векторами.
на плоскости
называются ее направляющими
векторами.
Эти
векторы являются базисными векторами
плоскости. Координаты векторов
и
обозначим переменными
 и
и
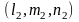 соответственно.
соответственно.

Z
2
1
O Y
X
Рис.3.9.
Пусть
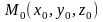 -
некоторая фиксированная точка на
плоскости
,
-
некоторая фиксированная точка на
плоскости
,
 -
произвольная точка этой плоскости (см.
рис.3.10).
-
произвольная точка этой плоскости (см.
рис.3.10).

Z

M0 M
 P
P
O Y
Рис.3.10.
X
Обозначим
координаты вектора
в базисе
 через
через
 ,
т.е.
,
т.е.
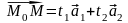 .
.
Тогда
из соотношения
 получим уравнение:
получим уравнение:
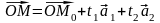 ,
,
которое
называется векторным
уравнением плоскости
.
Здесь
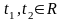 .
.
Записав координаты
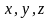 обеих частей векторного уравнения,
получим:
обеих частей векторного уравнения,
получим:
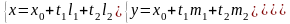
Эти уравнения называются параметрическими уравнениями плоскости.
Поскольку векторы , , - компланарны, то их смешанное произведение равно нулю:
 ,
,
следовательно, в координатной записи:

Это уравнение называется уравнением плоскости с направляющими векторами.
Пример
1. Найдем
уравнение плоскости, проходящей через
точку
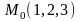 параллельно векторам
параллельно векторам
 и
и
 .
Подставив координаты точки и векторов
в определитель уравнения, получим:
.
Подставив координаты точки и векторов
в определитель уравнения, получим:
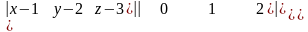 .
.
Разложив определитель по первой строке, получим искомое уравнение:


 .
.
5.
Пусть плоскость
проходит через три точки
,
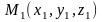 и
и
 ,
не лежащие на одной прямой. Тогда векторы
,
не лежащие на одной прямой. Тогда векторы
 и
и
 являются направляющими для плоскости
,
подставив их координаты в уравнение с
направляющими векторами, получим:
являются направляющими для плоскости
,
подставив их координаты в уравнение с
направляющими векторами, получим:
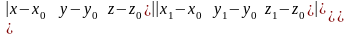 .
.
Это уравнение называется уравнением плоскости, проходящей через три заданные точки.
Пример
2. Найдем
уравнение плоскости, проходящей через
точки
 ,
,
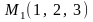 и
и
 .
Подставив координаты точек в уравнение,
получим:
.
Подставив координаты точек в уравнение,
получим:


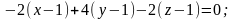
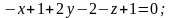
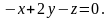
Несложно
проверить, что плоскость, описываемая
этим уравнением, проходит через точки
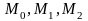 .
Для этого достаточно подставить
координаты точек в уравнение:
.
Для этого достаточно подставить
координаты точек в уравнение:

Разложив определитель в уравнении плоскости с направляющими векторами по первой строке, получим

Здесь
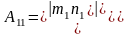
алгебраические
дополнения элементов первой строки.
Обозначив
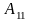 через
через
 ,
,
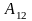 через
через
 ,
,
 через
через
 ,
а
,
а
 через
через
 ,
получим:
,
получим:
 .
.
Это уравнение называется общим уравнением плоскости.
Следующая теорема обосновывает это название.
Теорема.
Любая плоскость
в пространстве
определяется своим общим уравнением,
и любое уравнение вида
,
где
 ,
задает некоторую плоскость в пространстве.
,
задает некоторую плоскость в пространстве.
Доказательство первой части теоремы приведено выше, вторая часть теоремы дается без доказательства.
Заметим, что различные общие уравнения могут определять одну и ту же плоскость.
Определение. Вектор , перпендикулярный плоскости , называется нормальным вектором этой плоскости.
Теорема
о нормальном векторе плоскости. Вектор
с координатами
 является нормальным для плоскости
с уравнением
является нормальным для плоскости
с уравнением
в пространстве .
Докажите самостоятельно эту теорему, повторив с необходимыми изменениями доказательство для случая прямой.
Пример
3. Нормальным
вектором для плоскости
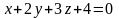 является вектор
является вектор
 .
.
Следствие 1. Косинус угла между плоскостями
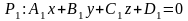 и
и

с нормальными векторами и находится по формуле:
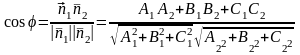 .
.
Следствие 2. Эти плоскости перпендикулярны только в том случае, когда
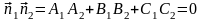 .
.
Следствие 3. Эти плоскости параллельны только в том случае, когда
.
Если же
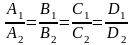 ,
,
то
плоскости
 и
и
 совпадают.
совпадают.
(Эти равенства здесь понимаются в смысле пропорций).
Пример
4. Найдем
косинус угла
между прямыми
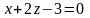 и
и
 .
Здесь
.
Здесь
 ,
,
 .
.
 .
.
Коэффициенты
нормального вектора
плоскости и коэффициент
позволяет оценить расположение плоскости
относительно координатных осей и
плоскостей следующим образом. (Во всех
уравнениях
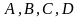 отличны от нуля).
отличны от нуля).
а)
Если
 ,
т.е. если уравнение плоскости
имеет вид:
,
т.е. если уравнение плоскости
имеет вид:

то
||
.
Это следует из того, что
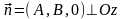 .
Плоскость вида
.
Плоскость вида
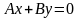 проходит через
,
т.к. координаты любой точки
вида
проходит через
,
т.к. координаты любой точки
вида
 удовлетворяют этому уравнению.
удовлетворяют этому уравнению.
в)
Плоскость с уравнением
 параллельна
,
а плоскость
параллельна
,
а плоскость
 проходит через
.
проходит через
.
с)
Плоскость с уравнением
 параллельна
,
а плоскость
параллельна
,
а плоскость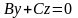 проходит через
.
проходит через
.
d)
Плоскость с уравнением
 параллельна плоскости
,
т.к. ее нормальный вектор
параллельна плоскости
,
т.к. ее нормальный вектор
 .
.
е)
Плоскость с уравнением
 параллельна
.
параллельна
.
f)
Плоскость с уравнением
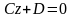 параллельна
.
параллельна
.
g)
Плоскость с уравнением
 проходит через начало координат точку
.
проходит через начало координат точку
.
7.
Пусть плоскость
проходит через точку
перпендикулярно вектору
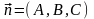 .
Возьмем на плоскости произвольную точку
M(x,y,z)
и составим вектор
.
Возьмем на плоскости произвольную точку
M(x,y,z)
и составим вектор
 =
= .
При любом расположении точки М на
плоскости вектора
и
.
При любом расположении точки М на
плоскости вектора
и
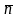 взаимно перпендикулярны, поэтому их
скалярное произведение равно нулю.
взаимно перпендикулярны, поэтому их
скалярное произведение равно нулю.
=0
Тогда
 .
.
Это уравнение называется уравнением плоскости с нормальным вектором.
Пример
4. Дана плоскость
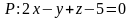 и точка
и точка
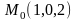 .
Найдем уравнение плоскости
||
и проходящей через точку
.
.
Найдем уравнение плоскости
||
и проходящей через точку
.
Поскольку
||
,
то вектор
 является нормальным для обеих плоскостей.
Подставляя его координаты и координаты
в уравнение, получим
является нормальным для обеих плоскостей.
Подставляя его координаты и координаты
в уравнение, получим

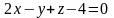 .
.
8.
Пусть плоскость
не проходит через начало координат и
пересекает оси
 в точках с координатами
в точках с координатами
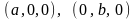 и
и
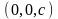 соответственно. Тогда уравнение этой
плоскости имеет вид:
соответственно. Тогда уравнение этой
плоскости имеет вид:
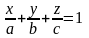 .
.
Это уравнение называется уравнением плоскости в отрезках
(см. рис.3.11).
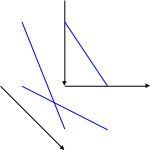 Z
Z
0
Y
X
Рис.3.11
Пример
5. Приведем
уравнение плоскости
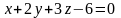 к виду уравнения в отрезках:
к виду уравнения в отрезках:

Следовательно,
эта плоскость пересекает координатные
оси в точках
 .
.
9.
Пусть плоскость
не проходит через начало координат, и
расстояние от точки
до
равно
,
и пусть
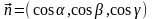 –
единичный нормальный вектор, проведенный
из точки
в направлении плоскости,
–
единичный нормальный вектор, проведенный
из точки
в направлении плоскости,
 – его направляющие косинусы.
– его направляющие косинусы.
Тогда уравнение этой плоскости имеет вид
 .
.
Это уравнение называется нормальным уравнением плоскости. Вывод уравнения с небольшими изменениями повторяет вывод нормального уравнения прямой.
Чтобы
из общего уравнения плоскости
 получить ее нормальное уравнение,
необходимо умножить его на число
получить ее нормальное уравнение,
необходимо умножить его на число
 ,
,
где знак берется противоположным знаком .
Пример
6. Нормальное
уравнение плоскости
 имеет вид
имеет вид
 .
.
Здесь
 .
.
Теорема.
Расстояние
от точки
до плоскости
 определяется формулой:
определяется формулой:
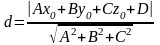 .
.
Пример
7. Напишем
уравнения плоскостей
и
,
параллельных плоскости
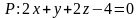 и находящихся на расстоянии
и находящихся на расстоянии
 от нее. Учитывая следствие, уравнения
плоскостей получим из соотношения:
от нее. Учитывая следствие, уравнения
плоскостей получим из соотношения:

Следовательно,

Определение.
Величина
 называется
отклонением
точки
от плоскости
.
называется
отклонением
точки
от плоскости
.
Плоскость
разбивает все пространство на два
полупространства, в одном из которых
положительно и совпадает с
,
а в другом
 и
.
Эти полупространства определяются
соответственно неравенствами:
и
.
Эти полупространства определяются
соответственно неравенствами:
 и
и
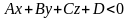 .
.
Несложно проверить, что нормальный вектор , проведенный из любой точки плоскости , указывает на полупространство .
