
- •Тема лекции: Аналитическая геометрия (3 часа) Аналитическая геометрия.
- •3.1 Прямая на плоскости
- •Уравнение прямой с угловым коэффициентом.
- •Теорема о нормальном векторе прямой. Вектор с координатами является нормальным для прямой с уравнением на плоскости .
- •3.2. Плоскость в пространстве
- •§ 3.3. Прямая в пространстве
- •Контрольные вопросы:
- •Литературы:
- •Тема лекции: Кривые второго порядка на плоскости. Поверхности второго порядка. (1 час)
- •Контрольные вопросы:
- •Литературы:
Тема лекции: Аналитическая геометрия (3 часа) Аналитическая геометрия.
3.1 Прямая на плоскости
В
этом параграфе мы рассмотрим различные
виды уравнений прямых на плоскости
 и
задачи, которые решаются с помощью этих
уравнений.
и
задачи, которые решаются с помощью этих
уравнений.
Уравнение прямой с угловым коэффициентом.
 у
у
М(х,у)
у-в
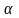
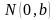
х
х
О
Рис.3.1
Прямая на оси Оу пересекает точку и с положительным направлением оси Ох составляет угол
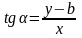 ;
;
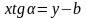 ;
;
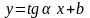
введем
обозначение
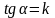 тогда
тогда
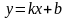
где
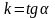 - называется угловым коэффициентом.
- называется угловым коэффициентом.
Пример
1. Уравнение
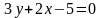 перепишем в виде
перепишем в виде
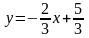 .
.
Следовательно,
это уравнение определяет прямую с
угловым коэффициентом
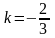 ,
пересекающую ось
,
пересекающую ось
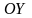 в точке с координатой
в точке с координатой
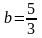 .
Для того, чтобы изобразить эту прямую
найдем ее точку пересечения с осью
.
Для того, чтобы изобразить эту прямую
найдем ее точку пересечения с осью
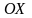 .
Подставив в уравнение
.
Подставив в уравнение
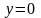 ,
получим что
,
получим что
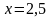 .
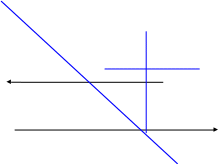
По точкам пересечения с осями координат
несложно построить эту прямую см. рис.
3.2.
.
По точкам пересечения с осями координат
несложно построить эту прямую см. рис.
3.2.
Y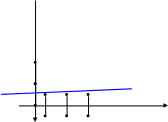
X
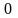
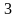
Рис. 3.2
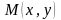
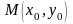
Если
прямая имеет угловой коэффициент
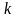 и проходит через данную точку
и проходит через данную точку
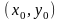 то
то
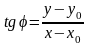 ,
,
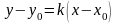 так как
,
то
так как
,
то
уравнение прямой через данную точку с угловым коэффициентом к имеет вид:
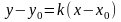
С помощью угловых коэффициентов можно определить углы между прямыми.
Из школьной программы известна следующая теорема.
Теорема.
Тангенс угла
между прямыми
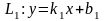 и
и
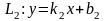 определяется формулой
определяется формулой
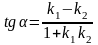
Прямые
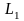 и
и
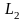 параллельны только в том случае когда
параллельны только в том случае когда
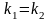
Прямые и перпендикулярны только в том случае, когда
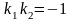
Пример
2. Для прямой
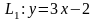 запишем уравнения прямых
||
и
запишем уравнения прямых
||
и
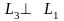 ,
проходящих через точку
,
проходящих через точку
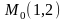 .
Прямая
имеет тот же угловой коэффициент, что
и
,
т.е.
.
Прямая
имеет тот же угловой коэффициент, что
и
,
т.е.
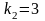 .
Поэтому ее уравнение имеет вид:
.
Поэтому ее уравнение имеет вид:
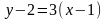 ,
т.е.
,
т.е.
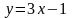 .
.
Прямая
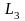 имеет угловой коэффициент
имеет угловой коэффициент
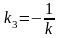 ,
т.е.
,
т.е.
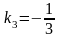 .
.
Ее уравнение записывается в виде:
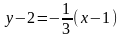 ,
т.е.
,
т.е.
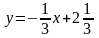 .
.
Определение. Любой ненулевой вектор
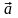 на прямой
на прямой
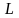 называется ее направляющим
вектором.
называется ее направляющим
вектором.
Этот
вектор является базисным вектором этой
прямой. Координаты
обозначим через
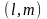 .
.
Y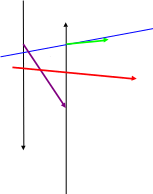
M0 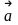 M
L
M
L
X
O
Рис. 3.3
Пусть
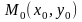 –
некоторая фиксированная точка на прямой
,
а
–
некоторая фиксированная точка на прямой
,
а
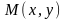 – произвольная точка на этой прямой
см. рис. 3.3. Обозначим координату вектора
– произвольная точка на этой прямой
см. рис. 3.3. Обозначим координату вектора
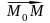 в базисе
через
в базисе
через
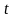 ,
т.е.
,
т.е.
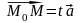 .
.
Тогда
из соотношения
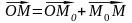 получим уравнение:
получим уравнение:
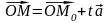 ,
,
которое называется векторным уравнением прямой .
Здесь
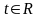 .
.
3. Запишем абсциссы и ординаты обеих частей векторного уравнения, получим:
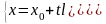
эти уравнения называются параметрическими уравнениями прямой на плоскости.
Поскольку векторы
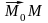 и
коллинеарные, то строки, составленные
из их координат
и
коллинеарные, то строки, составленные
из их координат
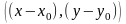 и
пропорциональны, следовательно,
и
пропорциональны, следовательно,
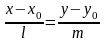
это уравнение называется уравнением прямой с направляющим вектором.
Пример
3. Напишем
уравнение прямой, проходящей через
точку
параллельно вектору
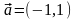 .
Подставим координаты точки и вектора
в уравнение, получим
.
Подставим координаты точки и вектора
в уравнение, получим
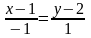 ;
;
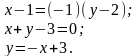
5.
Пусть прямая
проходит через
две точки
и
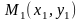 .
Тогда вектор
.
Тогда вектор
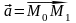 с координатами
с координатами
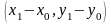 является направляющим для этой прямой.
является направляющим для этой прямой.
Поэтому, из уравнения с направляющим вектором получим, что
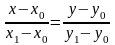
Это уравнение называется уравнением прямой, проходящей через две заданные точки.
Пример
4. Запишем
уравнение прямой, проходящей через
точки
и
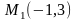 .
Подставив координаты точек в уравнение,
получим:
.
Подставив координаты точек в уравнение,
получим:
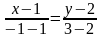
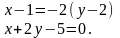
Раскрывая определитель в уравнении прямой с направляющим вектором, получим
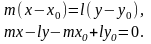
Обозначим
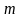 через А, –
через А, –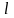 через
В,
через
В,
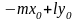 через С, в результате получим:
через С, в результате получим:
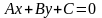 .
.
Это уравнение называется общим уравнением прямой.
Следующая теорема обосновывает это название.
Теорема.
Любая прямая
на плоскости
определяется своим общим уравнением и
любое уравнение вида
,
где
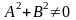 задает некоторую прямую на плоскости.
задает некоторую прямую на плоскости.
Доказательство. То, что уравнение любой прямой можно свести к общему виду, было показано выше. Докажем вторую часть теоремы. Пусть имеется уравнение
.
Если
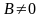 ,
то
,
то
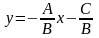 ,
что есть уравнение прямой с угловым
коэффициентом.
,
что есть уравнение прямой с угловым
коэффициентом.
Если
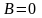 ,
то
,
то
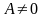 ,
получим:
,
получим:
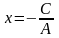 .
.
Это
уравнение определяет вертикальную
прямую, проходящую через точку
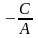 на оси
на оси
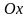 .
.
Не
следует думать, что между множеством
всех прямых на плоскости и множеством
всех общих уравнений имеется взаимно
однозначное соответствие. Например,
два уравнения
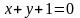 и
и
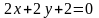 определяют одну и ту же прямую.
определяют одну и ту же прямую.
Определение.
Вектор
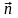 ,
перпендикулярный прямой
,
называется нормальным
вектором этой
прямой.
,
перпендикулярный прямой
,
называется нормальным
вектором этой
прямой.
