Примеры
В случайном порядке было отобрано 25 студентов экономического факультета и выписан их возраст:
19 17 22 18 17
17 23 21 18 19
17 22 18 18 18
20 17 19 21 17
21 17 18 23 18
Составить статистическое распределение студентов по возрасту. Построить полигон и кумуляту. Найти эмпирическую функцию распределения и дать ее графическое изображение.
Решение.
1. По исходным данным составим статистическое распределение выборки.
xi |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
mi |
7 |
7 |
3 |
1 |
3 |
2 |
2 |
2. Вычислим относительные частоты, и результаты вычислений внесем в третий столбец таблицы. Относительные частоты находим по формуле
.
В
данном случае объем выборки
.
Относительные частоты:
;
;
;
;
;
.
.
3. Вычислим накопленные частоты и результаты внесем в четвертый столбец таблицы.
;
;
;
;
;
;
.
Вычисленные относительные накопленные частоты указаны в пятом столбце таблицы.
варианты xi |
частоты mi |
относительные частоты,
|
накопленные частоты, |
относительные накопленные частоты |
17 |
7 |
0,28 |
7 |
0,28 |
18 |
7 |
0,28 |
14 |
0,56 |
19 |
3 |
0,12 |
17 |
0,68 |
20 |
1 |
0,04 |
18 |
0,72 |
21 |
3 |
0,12 |
21 |
0,84 |
22 |
2 |
0,08 |
23 |
0,92 |
23 |
2 |
0,08 |
25 |
1 |
4. Для построения полигона распределения отложим на оси абсцисс варианты xi, на оси ординат – частоты mi.
Для построения кумуляты отложим на оси абсцисс варианты xi, на оси ординат – накопленные частоты.
5. Найдем эмпирическую функцию F*(x) по данному распределению выборки.
Объем выборки .
Наименьшая
варианта
,
следовательно
,
при
.
Значение
,
а именно
наблюдалось 7 раз, следовательно
,
при
.
Значения
,
а именно
,
наблюдались
раз, следовательно
,
при
.
Аналогично,
при
;
,
при
;
,
при
;
,
при
.
Так как
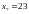– наибольшая варианта, следовательно
,
при
.
Эмпирическая функция имеет вид
Построим график этой функции
Наблюдения за жирностью молока у 50 коров дали следующие результаты (в %).
3,86 3,84 3,69 4,00 3,81 3,73 4,14 3,76
4,06 3,94 3,76 3,46 4,02 3,52 3,72
3,67 3,98 3,71 4,08 4,17 3,89 4,33
3,97 3,57 3,94 3,88 3,72 3,92 3,82
3,61 3,87 3,82 4,01 4,09 4,18 4,03
3,96 4,07 4,16 3,93 3,78 4,26 3,46
4,04 3,99 3,76 3,71 4,02 4,03 3,91
По этим данным построить интервальный вариационный ряд с равными интервалами и изобразить его графически (построить полигон, гистограмму, кумуляту).
Решение. 1. Выполним разбиение данного ряда на интервалы:
,
;
.
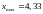Число
интервалов
;
длина
каждого интервала
;
за
начало первого интервала примем величину
.
жирность молока, интервал |
середина интервала, хi |
частота, mi |
относительная частота, |
накопленная частота, |
относительная накопленная частота |
3,40–3,54 |
3,47 |
2 |
2/50=0,04 |
2 |
0,04 |
3,54–3,68 |
3,61 |
4 |
4/50=0,08 |
6 (2+4) |
0,12 |
3,68–3,82 |
3,75 |
13 |
13/50=0,26 |
19 (6+13) |
0,38 |
3,82–3,96 |
3,89 |
11 |
11/50=0,22 |
30 (19+11) |
0,60 |
3,96–4,10 |
4,03 |
14 |
14/50=0,28 |
44 (30+14) |
0,88 |
4,10–4,24 |
4,17 |
4 |
4/50=0,08 |
48 (44+4) |
0,96 |
4,24–4,38 |
4,31 |
2 |
2/50=0,04 |
50 (48+2) |
1 |
2.
Для построения гистограммы откладываем
на оси абсцисс интервалы длинной
.
На этих интервалах построим прямоугольники
высотой, пропорциональной частоте. Для
построения полигона середины верхних
оснований соединим ломаной линией.
Для построения кумуляты на оси абсцисс отложим середины интервалов, а на оси ординат – накопленные частоты.
