Примеры

97. С помощью критерия Колмогорова на уровне значимости проверить гипотезу Н₀ о том, что случайная величина Х – выработка рабочих предприятия – имеет нормальный закон распределения.

выработка в отчетном году, %	94-100	100-106	106-112	112-118	118-124	124-130	130-136	136-142
количество рабочих, mi	3	7	11	20	28	19	10	2

Решение. 1. Построим эмпирическую и теоретическую функции распределения.

Эмпирическую функцию распределения строят по относительным накопленным частотам.

Теоретическую функцию распределения построим согласно формуле

где , ,

Результаты вычислений сведем в таблицу:

х	94	100	106	112	118	124	130	136	142
	0,01	0,03	0,10	0,21	0,41	0,69	0,88	0,98	1,00
	0,04	0,021	0,080	0,221	0,449	0,695	0,878	0,964	0,993
	0,006	0,009	0,02	0,011	0,039	0,005	0,002	0,016	0,007

Следовательно, ;

.

Критическое значение критерия Колмогорова равно (см. таблицу).

Так как 0,39<1,36 ( ), то гипотеза Н₀ согласуется с опытными данными.

6.6. Проверка гипотезы об однородности выборок

Гипотеза об однородности выборок – это гипотеза о том, что рассматриваемые выборки извлечены из одной и той же генеральной совокупности.

Пусть имеется две независимые выборки, произведенные из генеральных совокупностей с неизвестными теоретическими функциями распределения , проверяемая нулевая гипотеза имеет вид Н₀: против конкурирующей Н₁: .

Критерий Колмогорова-Смирнова

В критерии сравниваются две эмпирические функции распределения.

Статистика критерия Колмогорова-Смирнова имеет вид:

,

где и – эмпирические функции распределения, построенные по двум выборкам объемов n₁ и n₂.

Гипотеза отвергается, если , и принимается в противном случае.

Критерий Вилкоксона

Критерий Вилкоксона служит для проверки однородности двух независимых выборок: х₁, х₂, …, и у₁, у₂, …, Достоинство этого критерия состоит в том, что он применим к случайным величинам, распределения которых неизвестны.

Нулевая гипотеза Н₀: при всех значениях аргумента функции распределения равны между собой, т.е. .

Конкурирующими являются следующие гипотезы: гипотеза Н₁: , гипотеза Н₂: , гипотеза Н₃: .

а) Проверка нулевой гипотезы в случае, если объем обеих выборок не превосходит 25.

Правило 1. Конкурирующая гипотеза Н₁: .

1) Надо расположить варианты обеих выборок в возрастающем порядке, т.е. в виде одного вариационного ряда, и найти в этом ряду наблюдаемое значение критерия – сумму порядковых номеров вариант первой выборки.

2) Найти по таблице нижнюю критическую точку , где .

3)Найти верхнюю критическую точку по формуле .

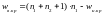Если или – нулевую гипотезу отвергают.

Если – нет оснований отвергать нулевую гипотезу.

Правило 2. Конкурирующая гипотеза Н₃: .

Надо найти , .

Если – нет оснований отвергать нулевую гипотезу.

Если – нулевую гипотезу отвергают.

Правило 3. Конкурирующая гипотеза Н₂: .

Надо найти верхнюю критическую точку:

.

Если – нет оснований отвергать нулевую гипотезу.

Если – нулевую гипотезу отвергают.

Замечание 1. Если несколько вариант только одной выборки одинаковы, то в общем вариационном ряду им приписывают обычные порядковые номера.

Замечание 2. Если совпадают варианты различных выборок, то им приписывают один и тот же порядковый номер, равный среднему арифметическому порядковых номеров, которые имели бы эти варианты до совпадения.

б) Проверка нулевой гипотезы в случае, если объем хотя бы одной из выборок превосходит 25.

Правило 1. Конкурирующая гипотеза: Н₁: .

Находят нижнюю критическую точку

, (6)

где [] – целая часть числа; ; находят по таблице функции Лапласа из равенства . В остальном сохраняются условия правила 1 из пункта а).

Правило 2. Конкурирующие гипотезы Н₃: и Н₂: .

Находят нижнюю критическую точку по формуле (6), положив и находят из равенства .

В остальном правила 2-3, приведенные в пункте а) сохраняются.