Глава 6. Проверка статистических гипотез

6.1. Статистическая гипотеза и общая схема ее проверки

Статистической гипотезой называют предположение относительно параметра известного распределения или о виде неизвестного распределения. При этом, проверяемую гипотезу (выдвинутую) называют нулевой (основной) и обозначают Н₀. Наряду с нулевой гипотезой Н₀ рассматривают ей противоречащую гипотезу, называемую альтернативной (конкурирующей) Н₁.

Различают простую и сложную статистические гипотезы. Гипотезу называют простой, если она содержит только одно предположение, и сложной, если она состоит из конечного или бесконечного числа простых гипотез.

Выдвинутая гипотеза может быть правильной или неправильной, поэтому возникает необходимость проверки гипотезы.

Суть проверки статистической гипотезы заключается в том, что используется специально составленная выборочная характеристика (статистика) , полученная по выборке х₁, х₂, …, х_n, точное или приближенное распределение которой известно. Затем по этому выборочному распределению определяется критическое значение Q_кр – такое, что если гипотеза Н₀ верна, то вероятность р( ) = α мала, так что в условиях данного исследования событие можно (с некоторым риском) считать практически невозможным. Поэтому, если обнаружится отклонение , то гипотеза Н₀ отвергается. Правило, по которому гипотеза Н₀ отвергается или принимается, называется статистическим критерием.

В итоге статистической проверки гипотезы могут быть допущены ошибки первого и второго рода. Ошибка I рода состоит в том, что правильная нулевая гипотеза Н₀ отвергается. Ошибка II рода заключается в том, что принимается неправильная нулевая гипотеза.

Вероятность совершить ошибку первого рода принято обозначать через ; второго рода – . Вероятность совершить ошибку первого рода называют уровнем значимости. Обычно уровень значимости принимают равным 0,05; 0,01; 0,005; 0,001.

Вероятность не допустить ошибку II рода, т.е. отвергнуть гипотезу Н₀, когда она неверна, называется мощностью критерия.

6.2. Проверка статистической гипотезы о том, что среднее значение генеральной совокупности на уровне значимости 

По выборке вычисляют значение статистики

1. Критическая область для проверки гипотезы, что среднее значение генеральной совокупности по сравнению с альтернативной на уровне значимости α определяется неравенством

где t_n-1;α отыскивается по таблице распределения Стьюдента (приложение 5).

2. Критическая область проверки гипотезы, что среднее значение генеральной совокупности по сравнению с альтернативной на уровне значимости α определяется неравенством

3. Критическая область для проверки гипотезы, что среднее значение генеральной совокупности по сравнению с альтернативной на уровне значимости α определяется неравенством

Если вычисленное значение статистики Т попадает в критическую область, то основная гипотеза отвергается. В этом случае принимается альтернативная гипотеза.

Примеры

92. Известно, что в среднем за смену на станке производится 110 деталей. Станок сломался и его отремонтировали. Проверить гипотезу об изменении производительности станка, если за 31 смену получены данные о производительности, для которых =100, Уровень значимости 0,05.

Решение. Нулевая гипотеза Н₀: , альтернативная гипотеза Н₁:

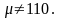
Найдем статистику

По таблице Стьюдента (приложение 2) находим

Так как –2,784 < –2,04 (Т <– ), следовательно, основная гипотеза не проходит, а проходит альтернативная гипотеза при уровне значимости =0,05.