5.3. Интервальные оценки

Выборка является образом генеральной совокупности, ее параметры – образами параметров всей генеральной совокупности. Вычисленные по выборке эмпирические числовые характеристики являются оценками этих характеристик всей генеральной совокупности. Если из той же генеральной совокупности сделаем другую выборку, то получим несколько иные значения. Следовательно, мы допускаем некоторую ошибку, находя точечную оценку. Чтобы избежать этого, строят интервальные оценки.

Интервальной оценкой называют такую оценку, которая определяется двумя числами, являющимися концами интервала, покрывающего оцениваемый параметр статистической совокупности.

Пусть – неизвестный параметр распределения, – найденная по данным выборки статистическая характеристика этого параметра. Тогда тем точнее определяет , чем меньше абсолютная величина разности

Надежностью (доверительной вероятностью) оценки называют вероятность 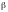, с которой осуществляется неравенство

Обычно в качестве берут числа, близкие к единице (чаще всего 0,9; 0,95; 0,98; 0,99; 0,9975).

или

.

Доверительным интервалом называют интервал , который покрывает неизвестный параметр с надежностью , где – предельная ошибка выборочной оценки.

1. Доверительный интервал для математического ожидания (а) при известном среднем квадратическом отклонении ( ) находится из условия:

, (2)

где n – объем выборки;

– выборочная средняя;

k_ – аргумент функции Лапласа, при котором .

Число определяется по таблице значений (приложение 4).

При этом называется точностью оценки. Выражение – средняя ошибка выборки или средняя ошибка репрезентативности.

2. Доверительный интервал для математического ожидания (а), если среднее квадратическое отклонение неизвестно, имеет вид

, (3)

где s – исправленное (несмещенное) среднее квадратическое отклонение,

t – определяется по таблице Стьюдента при числе степеней свободы и (приложение 6).

3. Доверительный интервал для оценки среднего квадратического отклонения σ нормального распределения

, (4)

где – определяется по таблице значений (приложение 6).

4. Интервальная оценка (с надежностью ) неизвестной вероятности р биноминального распределения имеет вид

, (5)

где - относительная частота;

n – общее число испытаний;

m – число появлений события в n испытаниях.

Примеры

87. Результат обследования 100 рабочих крупного завода, проводимого с целью определения времени, затрачиваемого на обработку детали, приведены в таблице

время обработки	3,6–4,2	4,2–4,8	4,8–5,4	5,4–6,0	6,0–6,6
число рабочих	14	33	35	12	6

Найти границы, в которых с надежностью 0,95 заключено среднее время обработки детали.

Решение. Для определения границ воспользуемся формулой (2). Для вычисления характеристик , k_ перейдем к серединам интервалов и таблица примет вид

xi	3,9	4,5	5,1	5,7	6,3
mi	14	33	35	12	6

,

=

=

=24,1956 – 23,7949 = 0,4007.

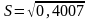=0,633.

Для определения k_ (по условию задачи ) определим

k_ =1,96 (приложение 4).

Тогда,

4,878 – 1,96· 4,878 + 1,96· ,

4,878 – 0,124 < а < 4,878 + 0,124,

4,754 < а < 5,002.

Итак, среднее время обработки детали заключено в интервале (4,75; 5,00).

88. Найти минимальный объем выборки, при котором с надежностью 0,975 точность оценки математического ожидания a генеральной совокупности по выборочной средней равна , если среднее квадратическое отклонение .

Решение. Точность оценки определяется формулой .

k_ = 2,24 (приложение 4).

Итак, =321,1264 n = 322.

89. Из генеральной совокупности извлечена выборка

xi	–2	1	2	3	4	5
mi	2	1	2	2	2	1

Оценить с надежностью 0,95 математическое ожидание а.

Решение. Объем выборки n = 10, следовательно, для интервальной оценки математического ожидания воспользуемся формулой (3):

– + .

=

(приложение 5).

Тогда,

2 – 2,26· 2 + 2,26·

2 – 1,718 < а < 2 + 1,718;

0,282 < а < 3,718.

90. Проведено 14 измерений одним прибором некоторой физической величины, s=0,86. Найти точность прибора с надежностью 0,99.

Решение. =0,99; n=14 q=0,78 (см. приложение 3).

Тогда, согласно формуле (4) получим

0,86(1 – 0,78) < σ < 0,86(1 + 0,78);

0,1892 < σ < 1,5308.

91. Изготовлен экспериментальный игровой автомат, который должен обеспечить появление выигрыша в одном случае из 100 бросаний монеты. Для проверки автомата произведено 400 испытаний, выигрыши появились 5 раз. Найти доверительный интервал, покрывающий известную вероятность с надежностью 0,999.

Решение. Применим формулу (3), для этого найдем относительную частоту появления выигрыша ; 1 – =1 – 0,0125=0,9875.

Найдем k_β из соотношения k_β =3,3 (приложение 4).

Воспользовавшись формулой (5), получим

< p < ;

0,0125 – 0,0183 < p < 0,0125 + 0,0183;

–0,0058 < p < 0,0308;

0 < p < 0,0308.