Тв и мс практикум

Глава 1. Случайные события

1.1. Классическое определение вероятности, геометрическая вероятность. Действия над событиями

Основные понятия в теории вероятностей это понятия события и вероятности события.

Событие – это какой-либо результат эксперимента или наблюдения (испытания), который может произойти или не произойти. Появление какого-либо конкретного результата в одном испытании называется элементарным исходом.

Все наблюдаемые события разделяют на 3 вида: достоверные, невозможные, случайные.

Достоверным называется событие, которое обязательно произойдет в результате данного опыта. Например, выпадение менее шести очков при подбрасывании игрального кубика.

Невозможным называется событие, которое не может произойти в результате данного опыта. Например, появление белого шара из ящика, в котором лежат синие, красные и черные шары.

Случайным называется событие, которое в результате данного опыта может произойти, а может и не произойти. Например, попадание в цель при одном выстреле.

Несовместными называются события, если появление одного из них исключает появление других событий в данном опыте. Например, извлечение стандартной и нестандартной детали при извлечении из ящика одной детали.

Равновозможными называются события, если нет оснований отдать предпочтение одному из них. Например, выпадение «орла» и «решки» при подбрасывании монеты.

Классическое определение вероятности

Вероятностью события A называется отношение числа m исходов, благоприятствующих этому событию, к числу n всех равновозможных несовместных элементарных исходов:

, где .

При решении вероятностных задач часто используются формулы комбинаторики:

1. Перестановка из п элементов есть упорядочение этих элементов, то есть расположение этих п элементов в определенном порядке.

Число перестановок определяется формулой

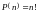
2. Размещение из п элементов по k – это любой выбор k элементов, взятых в определенном порядке.

Число размещений определяется формулой

.

3. Сочетание из п элементов по k – это любой выбор k элементов из п элементов безотносительно к порядку выбора.

Число сочетаний определяется формулой

.

Геометрическая вероятность

Пусть отрезок l составляет часть отрезка L. На отрезок L наудачу брошена точка. Вероятность попадания точки на отрезок l пропорциональна длине этого отрезка и не зависит от его расположения относительно отрезка L. Тогда вероятность попадания точки на отрезок l определяется равенством .

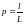Аналогично определяется вероятность попадания точки на фигуру f, составляющую часть фигуры F: и вероятность попадания точки в пространственную фигуру g, которая содержится в пространственной фигуре G: .

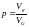Действия над событиями

Суммой двух событий A и B называется событие , состоящее в появлении события A или события B, или обоих вместе.

Произведением двух событий A и B называется событие , состоящее в совместном появлении события A и события B.

Теоремы сложения и умножения вероятностей

Теорема 1. Вероятность суммы несовместных событий равна сумме вероятностей этих событий

.

Теорема 2. Вероятность суммы совместных событий вычисляется по формуле

.

Теорема 3. Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что имело место первое событие

.

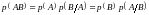Следствие. Если события A и B независимы, то .

Совокупность нескольких событий, из которых хотя бы одно обязательно появится при проведении испытания, называется полной группой событий. Два события, образующие полную группу, называются противоположными.

Сумма вероятностей противоположенных событий равна единице

.
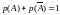