Одномерная и многомерная оптимизация
В MATLAB имеются функции для поиска минимума функции одной или нескольких вещественных переменных:
Для функции одной переменной используется функция fminbnd:
fminbnd(hFunction, x0, x1)
[xm,ym, flag,output]=fminbnd(f1,x0,x1)
где hFunction – дескриптор функции, для которой находится минимум, а x0 и x1 задают границы отрезка поиска, xm, ym значения минимума аргумента и функции, output – позволяет получить полную информацию о процессе нахождения минимума, в частности о количестве итераций.
Найдем
при помощи fminbnd
минимум
функции
,
» % задаем функцию
» f1=inline('1./((x-0.3).^2+0.01)+1./((x-0.9).^2+0.04)-6','x');
f1 = Inline function:
f1(x) = 1./((x-0.3).^2+0.01)+1./((x-0.9).^2+0.04)-6
где ./ – оператор поэлементное деления.
» % задаем на области исследования мелкую сетку для х
» xi=[0:0.01:3];
» % вычисляем функцию на этой сетке
» yi=feval(f1,xi);
» % строим график функции
» plot(xi,yi,'k:');
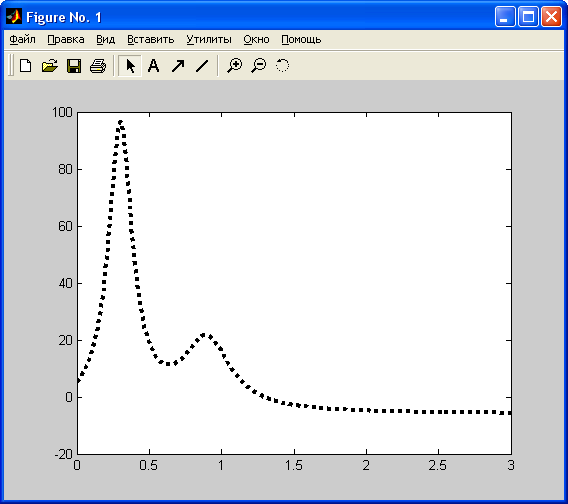
» % определяем локальный минимум функции на отрезке [0.5,1]
» xmin1=fminbnd(f1,0.5,1);
xmin1 = 0.6370
» % или с одновременным нахождением минимума и значения функции
» [xm,ym]=fminbnd(f1,0.5,1);
xm = 0.6370
ym = 11.2528
Для функции многих переменных используется функция fminsearch:
fminsearch(hFunction, x0)
[xm,ym,flag,output]=fminsearch(hFunction, x0)
где hFunction – дескриптор функции нескольких переменных, для которой находится минимум, а x0 – это вектор аргументов функции, с которого начинается поиск минимума.
Найдем
при помощи fminsearch
минимум функции
» % задаем функцию
» f2=inline('x(1).^2+x(2).^2','x');
f2 =
Inline function:
f2(x) = x(1).^2+x(2).^2
» % определяем минимум, задавая исходную точку x=1, y=1
» xmin=fminsearch(f2,[1 1]);
xmin =
1.0e-004 * % погрешность
-0.2102 0.2548 % искомое решение
Приложение 7
Основные математические функции в matlab
№ п/п |
Математическая функция |
Функция в MATLAB |
№ п/п |
Математическая функция |
Функция в MATLAB |
1 |
sin(x) |
sin(x) |
10 |
arcsin(x) |
asin(x) |
2 |
cos(x) |
cos(x) |
11 |
arccos(x) |
acos(x) |
3 |
tg(x) |
tan(x) |
12 |
arctg(x) |
atan(x) |
4 |
|
exp(x) |
13 |
sinh(x) |
sinh(x) |
5 |
ln(x) |
log(x) |
14 |
cosh(x) |
cosh(x) |
6 |
lg(x) |
log10(x) |
15 |
tgh(x) |
tgh(x) |
7 |
|
sqrt(x) |
16 |
arcsinh(x) |
asinh(x) |
8 |
|
x^2 |
17 |
arccosh(x) |
acosh(x) |
9 |
|
abs(x) |
18 |
arctgh(x) |
atanh(x) |
Редактор Т.А. Жирнова
ИД № 06039 от 12.10.01
Свод. темплан 2006 г.
Подписано в печать 25.07.06. Формат 60х84 1/16. Бумага офсетная.
Отпечатано на дупликаторе. Усл. печ. л. 5,0. Уч.- изд. л. 5,0.
Тираж Заказ .
Издательство ОмГТУ. 644050, Омск, пр. Мира, 11.
Типография ОмГТУ.