Интерполяция сплайнами
Под интерполяцией обычно подразумевают вычисление значений функции f(x) в промежутках между узловыми точками (линия функции получаемого интерполянта обязательно проходит через узловые точки).
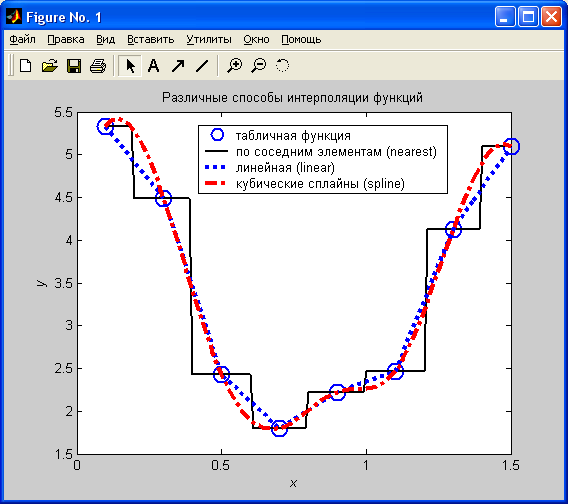
Простейшим способом интерполяции является аппроксимация данных сплайном нулевого порядка (на каждом участке степень полинома равна нулю), при котором значение функции в каждой промежуточной точке принимается равным ближайшему табличному значению. В результате данные приближаются ступенчатой функцией (интерполяция по соседним точкам). Линейная интерполяция основана на соединении соседних точек отрезками прямых (сплайн первого порядка). Для получения более гладкой функции применяют интерполяцию кубическими сплайнами.
Все эти способы реализованы в функциях: interp1 (одномерная), interp2 (двумерная), interp3 (трехмерная), interpn (многомерная).
yi = interp1(x,Y,xi)
yi = interp1(x,Y,xi,method)
yi = interp1(x,Y,xi) – строит кусочно-линейную интерполирующую кривую для одномерного массива Y, заданного на сетке х; выходной массив yi может быть определен на более мелкой сетке xi. Если Y – двумерный массив, то интерполирующая кривая строится для каждого столбца, тогда результирующий массив Yi будет иметь размер length(xi)×size(Y,2). Для значения xi вне области задания x присваивается значение NaN.
yi = interp1(x,Y,xi,method) – позволяет задать метод интерполяции.
В качестве метода может быть использованы:
'nearest' – ступенчатая интерполяция (по соседним элементам);
'linear' – линейная интерполяция (принимается по умолчанию, если способ не задан);
'spline' – кубические сплайны;
'pchip' – интерполяция кубическими эрмитовыми сплайнами (вторая производная сплайна (в отличии от spline) может быть разрывна, т.е. сплайн имеет дефект два) .
Рассмотрим применение приближения данных с использованием функции interp1(x,Y,xi,method) на примере тех же данных.
» x=[0.1:0.2:1.5];
» y=[5.332 4.488 2.432 1.803 2.223 2.467 4.127 5.091];
» xi=[0.1:0.01:1.5];
» % вычисление ступенчатой функции в промежуточных точках
» ynear = interp1(x,y,xi,'nearest');
» % вычисление кусочно-линейной функции в промежуточных точках
» yline = interp1(x,y,xi,'linear'); % можно не указывать 'linear'
» % вычисление кубического сплайна в промежуточных точках
» yspline = interp1(x,y,xi,'spline');
» hold on;
» % построение графиков интерполянтов
» plot(x, y, 'ko',xi, ynear, 'k', xi, yline, 'k:', xi, yspline, 'k-.');
» legend('табличная функция', 'по соседним элементам (nearest)', ...
'линейная (linear)', 'кубические сплайны (spline)',4);
» title('Различные способы интерполяции функций');
Аппроксимация данных при помощи регрессии
Для решения задачи обобщенной нелинейной регрессии в MATLAB имеется функция lsqnonlin(), возвращающая решение задачи нахождения точки минимума функции f(x)
где в общем случае f(x) – вектор-функция, х – вектор-столбец искомых переменных, L – некоторая константа.
Синтаксис функции lsqnonlin():
x = lsqnonlin(fun, x0)
x = lsqnonlin(fun, x0, lb, ub)
x = lsqnonlin(fun, x0, lb, ub, options)
x = lsqnonlin(fun, x0, lb, ub, options, P1, P2, … ),
здесь
fun – название минимизируемой функции;
х0 – начальная точка, с которой начинается процесс поиска минимума функции;
lb, ub – соответственно левая и правая границы отрезка, на котором определяется минимум функции;
options – параметр, задающий режим работы функции оптимизирующей функции (перечень возможных значений данного параметра приведен в Help MATLAB в главе Optimization Toolbox в разделе Optimization Parameters);
P1, P2, … – параметры, от которых зависит функция fun.
Рассмотрим
пример, демонстрирующий использование
данной функции для нахождения
параметров функции
» % листинг m-файла FABXCX2;
function z=FABXCX2(Coeff,vx,vy);
k=1:length(vx);
z=vy–exp(Coeff(1)+Coeff(2)*vx+Coeff(3)*vx.^2);
где оператор .^ – означает поэлементное возведение в степень
» % листинг команд
» x=[0.1:0.2:1.5];
» y=[5.332 4.488 2.432 1.803 2.223 2.467 4.127 5.091];
» xi=[0.1:0.01:1.5];
» z=[1 0 –1]; % начальное приближение
z= 1 0 –1
» % вычисление коэффициентов аппроксимирующей функции
» Coeff = lsqnonlin('FABXCX2',z,[],[],[],x,y);
Maximum number of function evaluations exceeded;
increase options.MaxFunEvals
Coeff = 1.9480 –2.6658 1.6461
» % задаем аппроксимирующую функцию
» F=inline('exp(a+b*x+c*x.^2)','x','a','b','c');
» % вычисление аппроксимирующей функции
» yi=feval(F,xi,Coeff(1),Coeff(2),Coeff(3));
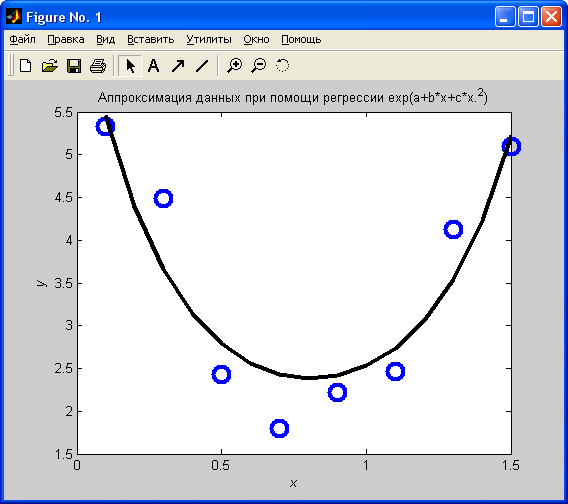
» plot(x, y, 'ko',xi, yi, 'k');
» title('Аппрокcимация данных при помощи регреccии exp(a+b*x+c*x.^2)');
» xlabel('\itx');
» ylabel('\ity');
Приложение 6