
- •Математические методы моделирования физических процессов
- •Введение
- •Лабораторная работа № 1 численное решение обыкновенных дифференциальных уравнений первого порядка
- •Порядок выполнения работы
- •Лабораторная работа № 2 численное решение ду высших порядков или систем оду
- •Порядок выполнения работы
- •Лабораторная работа № 3 численное решение краевых задач
- •Порядок выполнения работы
- •Лабораторная работа № 4 численное решение дифференциальныхных уравнений в частных производных
- •Порядок выполнения работы
- •Лабораторная работа № 5 численное решение систем линейных алгебраических уравнений
- •Порядок выполнения работы
- •Лабораторная работа № 6 численное решение нелинейных уравнений и их систем
- •Порядок выполнения работы
- •Лабораторная работа № 7 аппроксимация данных методом наименьших квадратов
- •Порядок выполнения работы
- •Лабораторная работа № 8 решение задач одномерной и многомерной оптимизации
- •Порядок выполнения работы
- •Библиографический список
- •Приложения
- •Первые навыки работы в matlab
- •Численное решение оду и их систем
- •Численное решение краевых (граничных) задач
- •Аналитическое решение линейных сиситем алгебраических уравнений
- •Численное решение линейных или нелинейных систем алгебраических уравнений
- •Аппроксимация данных
- •Приближение данных полиномом
- •Интерполяция сплайнами
- •Аппроксимация данных при помощи регрессии
- •Одномерная и многомерная оптимизация
- •Основные математические функции в matlab
Численное решение линейных или нелинейных систем алгебраических уравнений
Команда FSOLVE – решает численно систему линейных или нелинейных уравнений F(X)=0 , где X – вектор, а F(X) – функция, которая возвращает значение вектора.
X = fsolve (fun, x0)
X = fsolve (fun, x0, options)
X = fsolve (fun, x0, options, P1, P2...)
[X, fval] = fsolve (...)
[X, fval, exitflag] = fsolve (...)
[X, fval, exitflag, output, jacobian] = fsolve (...)
X = fsolve (fun, x0) – начинается в x0 и пытается решить уравнения, описанные в fun;
X = fsolve (fun, x0, options) – решая уравнения, описанные в fun, минимизирует погрешность с параметрами оптимизации, указанными в структуре options (используйте команду optimset, чтобы установить эти параметры);
X = fsolve (fun, x0, options, P1, P2...) – дает решение, подобное описанному выше, передавая дополнительные параметры p1, р2, ... в m-файл F всякий раз, когда он вызывается (вычисление функций fun). Используйте options=[], если никакие параметры не задаются (опции используются по умолчанию);
[X, fval] = fsolve (...) – кроме решения X возвращает в fval значение fun функции для полученного решения Х.
[X, fval, exitflag] = fsolve (...) – дополнительно возвращает значение exitflag, который описывает условие (состояние) выхода.
[X, fval, exitflag, output] = fsolve (...) – дополнительно возвращает структуру output, которая содержит информацию об оптимизации.
[X, fval, exitflag, output, jacobian] = fsolve (...) – дополнительно возвращает Якобиан для fun при решении.
Команда OPTIMSET – задает, изменяет или выводит структуру свойств (опций) для решателя FSOLVE систем алгебраических уравнений F(X)=0:
options = optimset('param1',value1,'param2',value2,...)
options = optimset
options = optimset(optimfun)
options = optimset(oldopts,'param1',value1,...)
options = optimset(oldopts,newopts)
optimset
options = optimset('param1',value1,'param2',value2,...) – формирует массив параметров (структуру) options, в котором параметрам (опциям) с именами 'param1', 'param2', … приписываются некоторые значения value1, value2,…(достаточно указать только первый символ); неприсвоенному значению приписывается пустой массив [];
options = optimset – формирует массив параметров (структуру) options, в котором всем параметрам устанавливаются значения [];
options = optimset(optimfun) – формируется массив параметров options из всех возможных параметров, значения которых выбираются так, чтобы оптимизировать функцию optimfun;
options = optimset(oldopts,'param1',value1,...) – заменяет значения отдельных свойств (опций);
options = optimset(oldopts,newopts) – заменяется набор старых свойств набором новых, но если при этом для какого-либо из новых свойств указано [], то сохраняется прежнее значение этого свойства;
optimset – выводит список всех параметров (опций) с указанием их возможных значений и значений по умолчанию в фигурных скобках.
Параметры
Свойство |
Значение |
Описание |
Display |
'off' 'iter' 'final' notify' |
Уровень показа: 'off' не показывает ничего; 'iter' показывает при каждом повторении; 'final' показывает конечный результат; 'notify' показывает выходящее значение, если только функция не сходится |
MaxFunEvals |
положительное целое число |
Максимальное число позволенных оценок функции |
MaxIter |
положительное целое число |
Максимальное число позволенных повторений |
TolFun |
положительный скаляр |
Подходящий предел значения функции |
TolX |
положительный скаляр |
Подходящий предел x |
Границы погрешностей интегрирования
Свойство |
Значение |
Описание |
DerivativeCheck |
'on' | {'off'} вкл | {выкл} |
Сравните указанные пользователем аналитические производные (градиенты или функциональный определитель(якобиан)) с конечными различными производными. |
Дополнительные характеристики
Свойство |
Значение |
Описание |
1 |
2 |
3 |
Diagnostics |
'on' | {'off'} вкл | {выкл} |
Показывает диагностическую информацию о функции, которая будет минимизирована или решена |
DiffMaxChange |
положительный скаляр | {1e-1}
|
Максимальные изменения в переменных для конечных различных производных |
DiffMinChange |
положительный скаляр | {1e-8}
|
Минимальные изменения в переменных для конечных различных производных |
GoalsExactAchieve |
положительное скалярное целое число | {0} |
Число точно достигнутых значений |
GradConstr |
'on' | {'off'} вкл | {выкл} |
Градиенты для нелинейных ограничений, определенных пользо-вателем |
GradObj |
'on' | {'off'} вкл | {выкл} |
Градиент(ы) для объективной функции(й), определенной пользователем |
Hessian |
'on' | {'off'} вкл | {выкл} |
Определитель Гессе для объективной функции, определенной пользователем |
HessMult |
функция | {[]}
|
Определитель Гессе умножает функцию, указанную пользователем |
HessPattern |
редкая матрица | {редкая матрица всех}
|
Разряженный образец определителя Гессе для конечной разного. Размером матрицы – n-на-n, где n – число (номер) элементов в x0, начальной точке |
HessUpdate |
{'bfgs'} | 'dfp' | 'gillmurray' | 'steepdesc' |
Квази–Ньютон, обновляющий схему |
Jacobian |
'on' | {'off'} вкл | {выкл} |
Функциональный определитель (Якобиан) для объективной функции, определенной пользо-вателем |
JacobMult |
функция | {[]}
|
Функциональный определитель (Якобиан) умножает функцию, определенную пользователем |
1 |
2 |
3 |
JacobPattern |
редкая матрица | {редкая матрица всех}
|
Разряженный образец функционального определителя (Якобиана) для конечного различного. Размер матрицы – m-на-n, где m. - число величина в первом аргументе, указанная пользователем возвращенной функции fun, и n – число элементов в x0, начальной точке |
LargeScale |
вкл | {выкл} |
Используйте крупномасштабный алгоритм если возможно. Исключение: постороннее значение для fsolve 'выключен' |
LevenbergMarquardt |
вкл | {выкл} |
Предпочитает Левенберг-Марквардт алгоритму Гаусс-Ньютона |
LineSearchType |
'cubicpoly' | {'quadcubic'} |
Выбор алгоритма поиска линии |
MaxPCGIter |
положительное целое число |
Максимальное число (номер) PCG позволенных повторений. Пользовательское значение больше 1 и нижнее (n/2)), где n – число (номер) элементов в x0, начальной точке |
MeritFunction |
'singleobj' | {'multiobj'} |
Использование значений достигших min/max присваивает данной функции (многопеременную) против fmincon |
MinAbsMax |
положительное скалярное целое число | {0} |
Уменьшается худший результат функции F(x) |
PrecondBandWidth |
положительное целое число | {0} | Inf |
Верхняя полоса пропускания предусловия для PCG |
TolCon |
положительный скаляр |
Предел терпимости при нарушении ограничения |
TolPCG |
положительный скаляр | {0.1} |
Предел терпимости завершения на PCG повторении |
TypicalX |
вектор всех |
Типичные значения x. Длина вектора равна числу (номеру) элементов в x0, начальной точке |
При численном решении средствами MATLAB системы СЛАУ
2,74x1 -1,18 x2 +3,17 x3 =2,18,
0,18x1 +1,27x2 +0,76x3 =3,23,
1,12x1 + 0,83x2 -2,16 x3 =-1,15
получаем для m-файла LR32.m
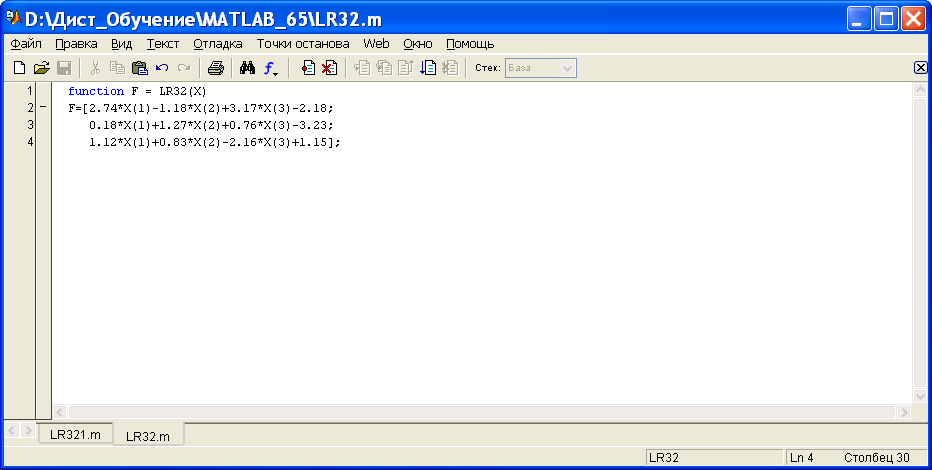
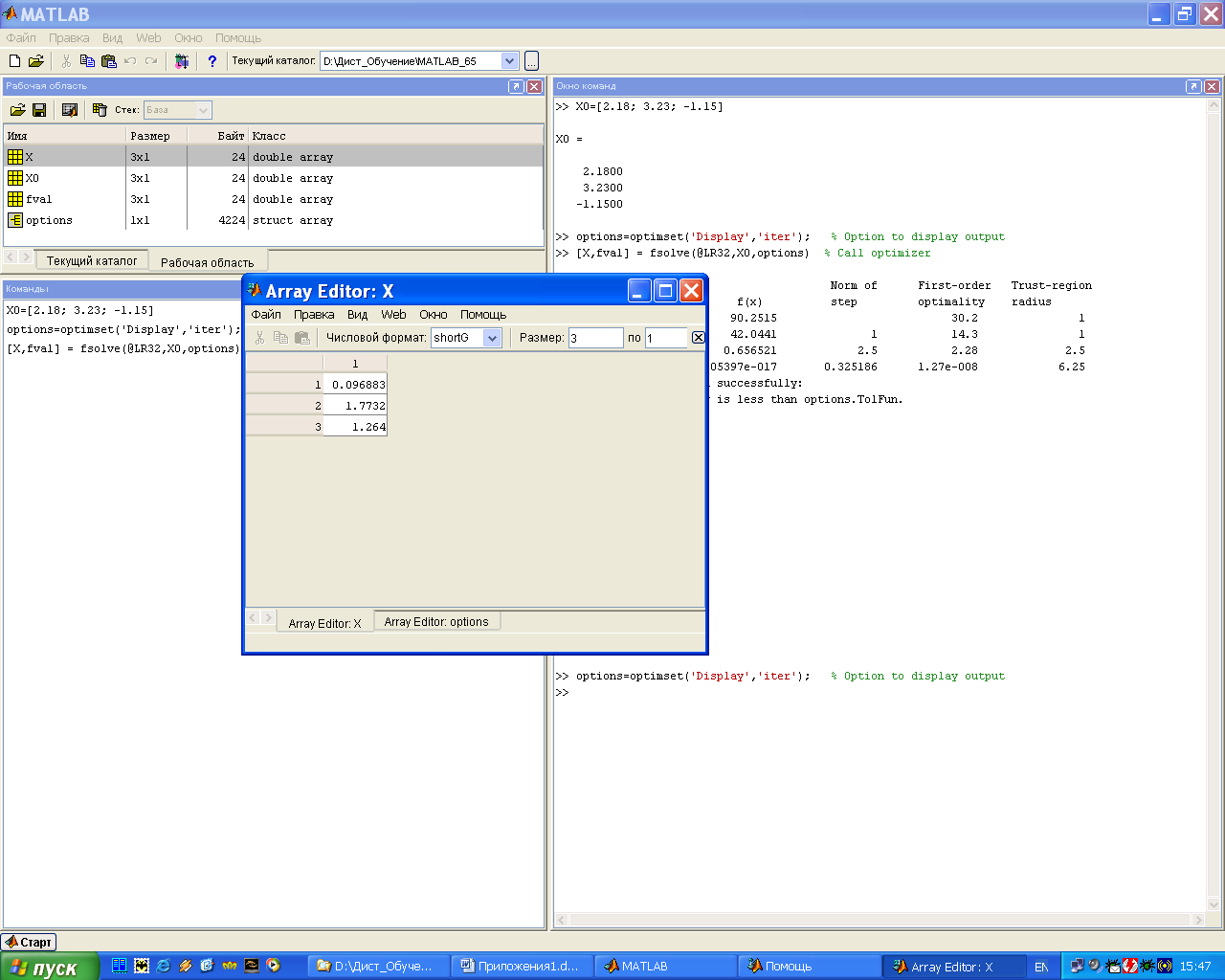
Тогда в окне команд MATLAB выполняем команды
»X0=[2.18; 3.23; -1.15]; % Vektor-stolbec 1-oe priblizenie
»options=optimset('Display','iter'); % Option to display output
»[X,fval] = fsolve(@LR32,X0,options); % Call optimizer
Norm of First-order Trust-region
Iteration Func-count f(x) step optimality radius
1 4 90.2515 30.2 1
2 8 42.0441 1 14.3 1
3 12 0.656521 2.5 2.28 2.5
4 16 2.05397e-017 0.325186 1.27e-008 6.25
Optimization terminated successfully:
First-order optimality is less than options.TolFun.
Ответ: X =[0.0969; 1.7732; 1.2640]
fval = 1.0e-008 *[0.3612; 0.1543; 0.2261]
При численном решении средствами MATLAB системы нелинейных алгебраических уравнений вида

Получаем M-файл в виде:
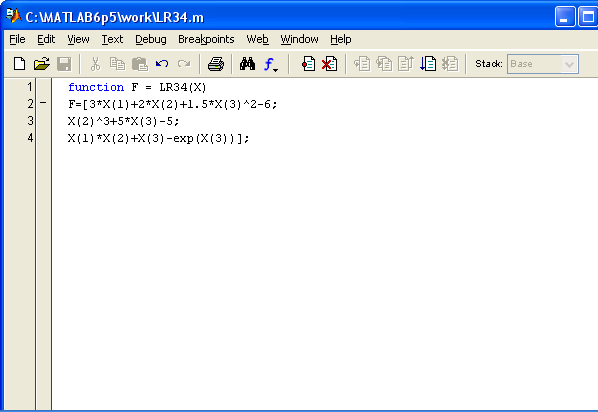
Тогда в окне команд MATLAB выполняем
»X0=[-6; -5; 0]; % Vektor-stolbec 1-oe priblizenie
»options=optimset('Display','iter'); % Option to display output
»[X,fval] = fsolve(@LR34,X0,options); % Call optimizer
И получаем ответ в окне команд:
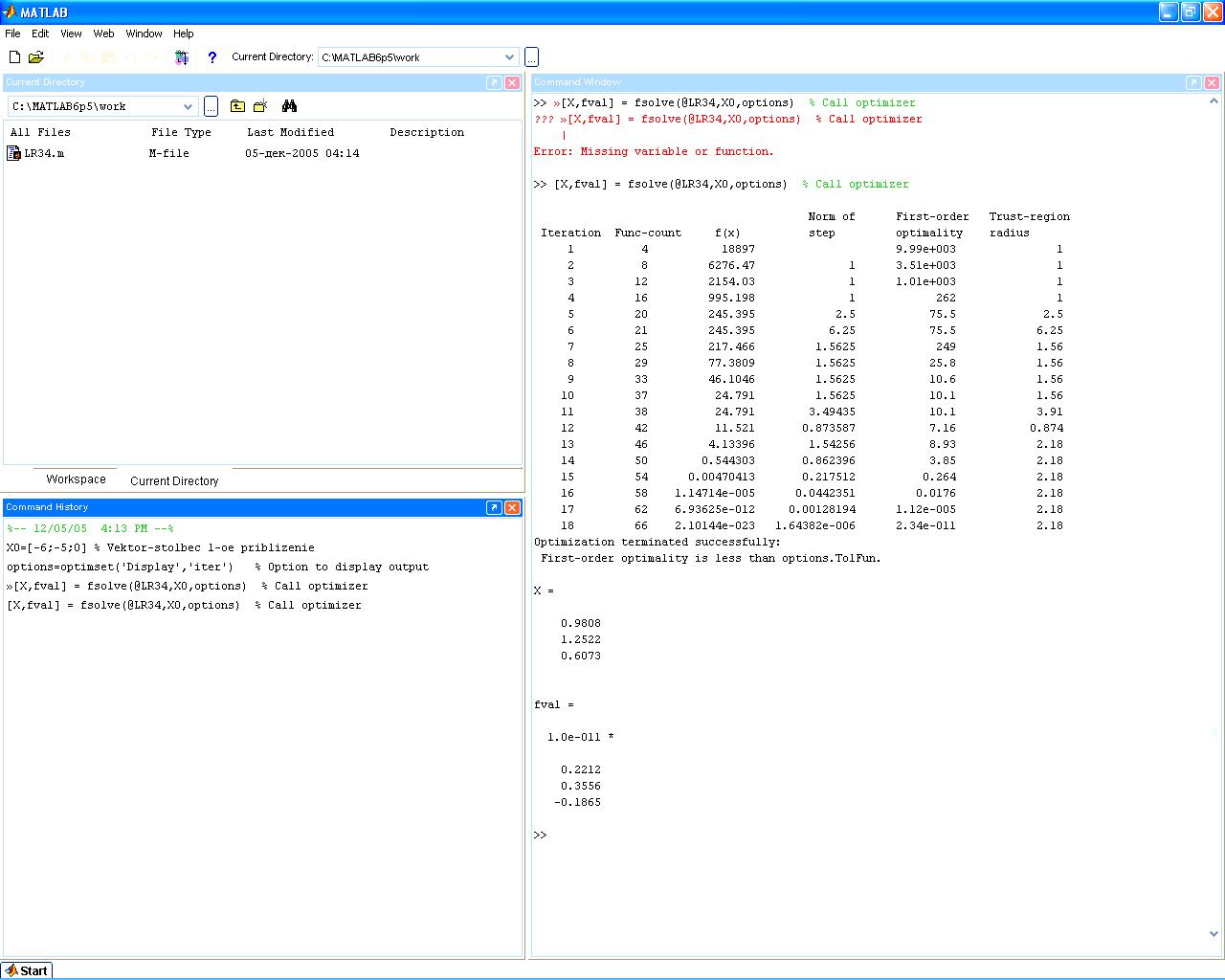
Приложение 5
