Аналитическое решение линейных сиситем алгебраических уравнений

В MATLAB для реализации различных алгоритмов решения СЛУ и связанных с ними матричных операций применяются следующие операторы: +, -, *, /, \, *, '. MATLAB имеет два различных типа арифметических операций - поэлементные и для массивов (векторов и матриц) в целом. Матричные арифметические операции определяются правилами линейной алгебры.

Арифметические операции сложения и вычитания над массивами выполняются поэлементно. Знак точки «.» отличает операции над элементами массивов от матричных операций. Однако поскольку операции сложения и вычитания одинаковы для матрицы и элементов массива, знаки «.+» и «.-» не используются. Рассмотрим другие операторы и выполняемые ими операции.

• * — матричное умножение;

• С = А*В — линейное алгебраическое произведение матриц А и В:

Для случая не скалярных А и В число столбцов матрицы А должно равняться числу строк матрицы В. Скаляр может умножаться на матрицу любого размера.

• / – правое деление. Выражение Х=В/А дает решение ряда систем линейных уравнений АХ=В, где А — матрица размера тхп и В – матрица размера nxk;

• \ – левое деление. Выражение Х=В\А дает решение ряда систем линейных уравнений ХА=В, где А – матрица размера тхп и В – матрица размера nxk. Если А – квадратная матрица, то А\В – примерно то же самое, что и inv(A)*B, в остальных случаях возможны варианты, отмеченные ниже.

Если А – матрица размера пхп, а В – вектор-столбец с п компонентами или матрица с несколькими подобными столбцами, тогда Х=А\В – решение уравнения АХ=В, которое находится хорошо известным методом исключения Гаусса.

Если А – матрица размера тхп и тхп, а В представляет собой вектор-столбец с m компонентами или матрицу с несколькими такими столбцами, тогда система оказывается недоопределенной или переопределенной и решается на основе минимизации второй нормы невязок.

• ^ – возведение матрицы в степень. Х^р – это X в степени р, если р – скаляр. Если р – целое число, то степень матрицы вычисляется путем умножения X на себя р раз. Если р – целое отрицательное число, то X сначала инвертируется. Для других значений р вычисляются собственные значения и собственные векторы, так что если [V,D]=eig(X), то X*p=V*D. ^p/V. Если X – скаляр и Р – матрица, то Х^Р – это скаляр X, возведенный в матричную степень Р. Если X и Р – матрицы, то Х^Р становится некорректной операцией и система выдает сообщение об ошибке. Возможный вариант решения матричного уравнения АХ=В с применением оператора ^{^} можно представить как Х=В*А^{^}-1.

• ' – транспонирование матрицы, то есть замена строк столбцами и наоборот. Например, А' – транспонированная матрица А. Для комплексных матриц транспонирование дополняется комплексным сопряжением. Транспонирование при решении СЛУ полезно, если в матрице А переставлены местами столбцы и строки.

При аналитическом решении средствами MATLAB системы СЛАУ

2,74x₁ -1,18 x₂ +3,17 x₃ =2,18,

0,18x₁ +1,27x₂ +0,76x₃ =3,23,

1,12x₁ + 0,83x₂ -2,16 x₃ =-1,15.

получаем

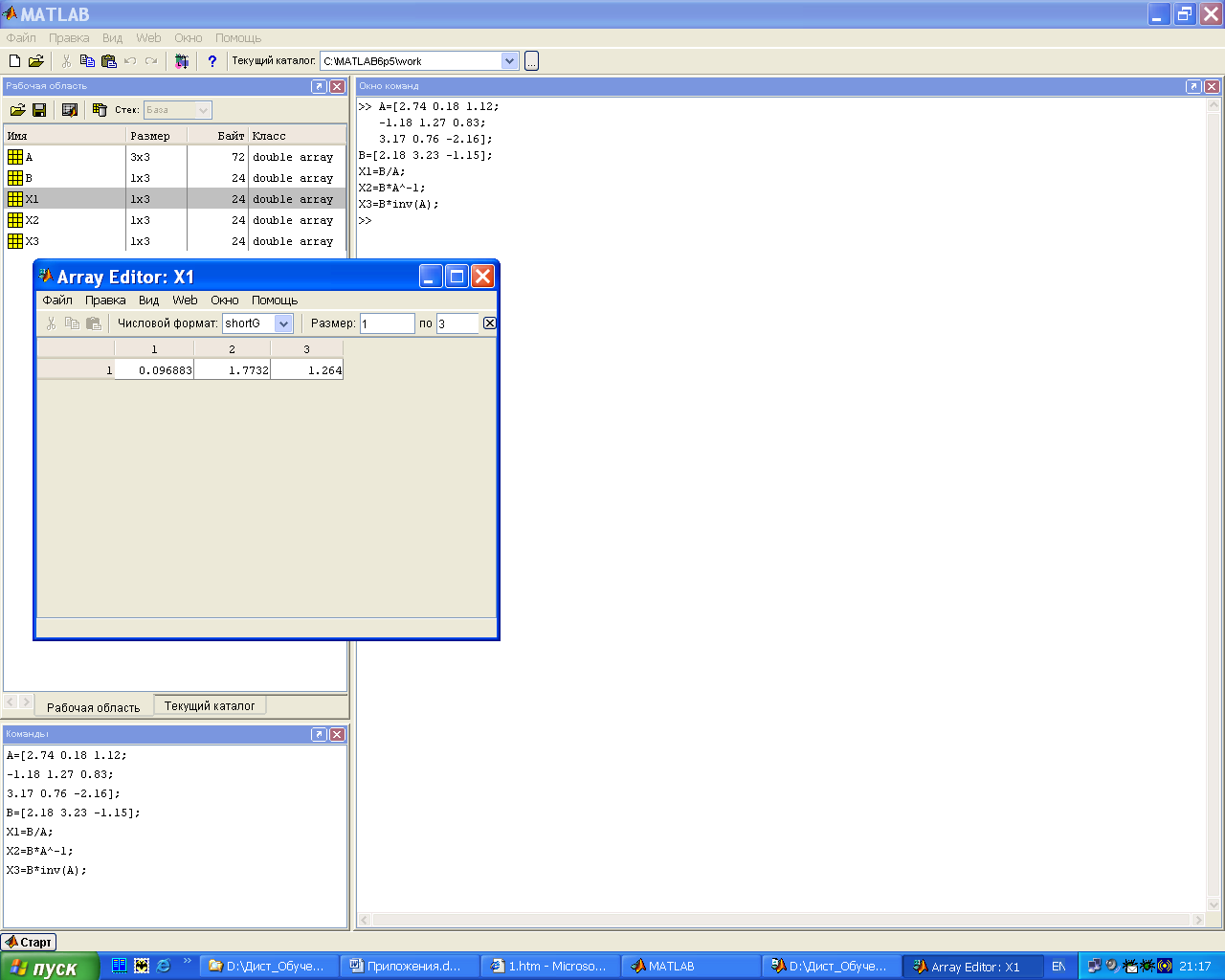
Решение может быть найдено тремя способами:

X1=B/A;

X2=B*A^-1;

X3=B*inv(A);

В качестве ответа получаем, например для Х1=(0.096883, 1.7732, 1.264).