Приложения

Приложение 1

Элементы рабочей среды MATLAB

Основными элементами рабочей среды MATLAB являются:

1) меню;

2) панель инструментов с кнопками и раскрывающимся списком;

3) окно Рабочая область (Workspace) для просмотра переменных (результаты расчетов);

4) окно Текущий каталог (Current Directory) для установки текущего каталога (При использовании m-файлов необходимо, чтобы они находились в текущем каталоге);

5) окно Команды (Command History) для просмотра и повторного выполения ранее введенных команд;

6) окно Окно команд (Command Window) для ввода команд и вывода результатов;

7) строка состояния с кнопкой Старт (Start)

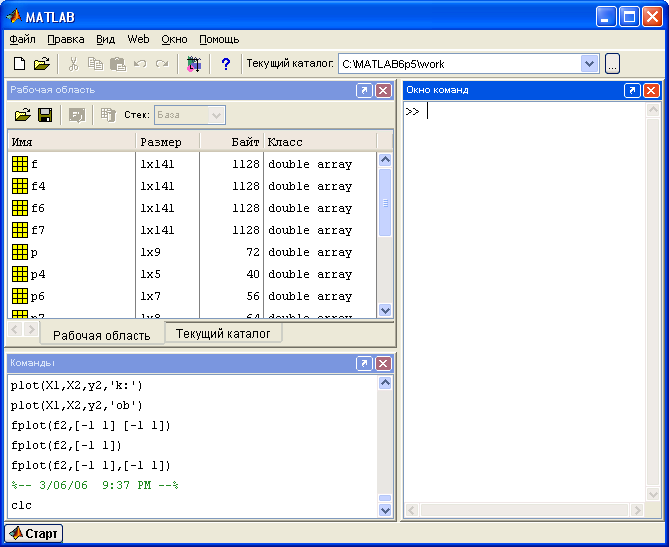
При нажатии на кнопку Старт открывается меню, с помощью которого обеспечивается доступ ко всем основным средствам MATLAB.

Приложение 2

Первые навыки работы в matlab

1. Текстовые комментарии вводятся в Окне команд с помощью символа %. Рекомендуется не использовать русское «с» (этот символ переводит на следующую строчку), а при необходимости применять английское «с», что на виде текстового комментария никак не сказывается.

2. Оператор – это специальное обозначение для определенной операции над данными – операндами. Например, простейшими арифметическими операторами являются знаки суммы +, вычитания –, умножения * и деления /. Операторы используются совместно с операндами. Например, в выражении 2+3 знак + является оператором сложения, а числа 2 и 3 – операндами. Следует отметить, что большинство операторов относится к матричным операциям, что может служить причиной серьезных недоразумений. Например, операторы умножения * и деления / вычисляют произведение и частное от деления двух многомерных массивов, векторов или матриц. Есть ряд специальных операторов, например, оператор \ означает деление справа налево, а операторы .* и ./ означают соответственно поэлементное умножение и поэлементное деление массивов.

Следующие примеры поясняют сказанное на примере операций с векторами:

» Vl=[2 4 6 8]; % присваиваем вектору V1 значения

» V2=[l 2 3 4]; % присваиваем вектору V1 значения

» V1/V2 % векторное деление

ans = 2 % ответ

» V1.*V2; % поэлементное умножение

ans=2 8 18 32

» V1./V2; % поэлементное деление

аns =2 2 2 2

3. Очень часто необходимо произвести формирование упорядоченных числовых последовательностей. Такие последовательности нужны для создания векторов или значений абсциссы при построении графиков (для организации сплошной линии графика шаг рекомендуется 0.01). Для этого в MATLAB используется оператор : (двоеточие): Начальное значение: Шаг: Конечное значение Данная конструкция порождает возрастающую последовательность чисел, которая начинается с начального значения, идет с заданным шагом и завершается конечным значением. Если Шаг не задан, то он принимает значение 1. Если конечное значение указано меньшим, чем начальное значение – выдается сообщение об ошибке. Примеры применения оператора двоеточие даны ниже:

» 1:5;

ans =12345

» xi=0:0.2:1;

xi = 0 0.2 0.4 0.6 0.8 1

Приложение 3