Порядок выполнения работы

1. Разработать программу для решения нелинейного уравнения или СНЛУ одним из описанных выше методов (например, на алгоритмическом языке Pascal) и провести численное моделирование с получением приближенного (~) значения искомого решения .

2. Решить эту же задачу средствами MATLAB (примеры решения систем нелинейных уравнений см. в прил. 4), где в качестве результатов «точного» эксперимента получить искомое решение .

3. Оценить точность полученной модели.

Варианты заданий

Задание 6.1. Решить уравнение f(x)=0 одним из методов (=110^-3).

№ п/п	f(x)	Отрезок	№ п/п	f(x)	Отрезок
1		[0, 6]	16	4-x-4/x2	[1, 4]
2	x2+16/x-16	[1, 4]	17		[-3, 3]
3		[0; 4]	18		[-1; 5]
4		[1; 9]	19	10x/(x2+1)-3	[0; 3]
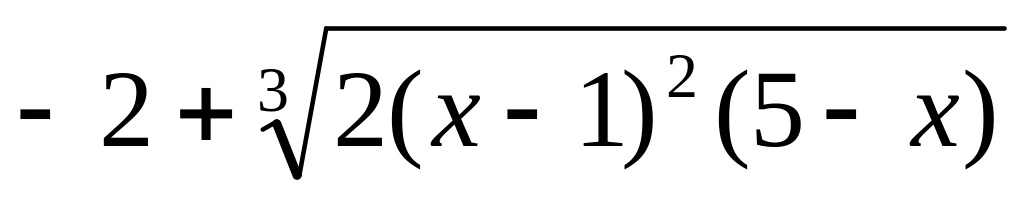
5		[-3; 3]	20	2x2+108/x2-59	[2; 4]
6	2-x-4/(x+2)2	[-1; 2]	21		[-1; 6]
7		[1; 4]	22		[-1; 7]
8		[1; 5]	23	4x/(x2+4)	[-4; 2]
9	-x2/2+8/x+8	[-4; -1]	24		[-2; 4]
10		[-2; -1]	25		[-5; 2,8]
11	2-x-4/(x+1) 2	[-1; 2]	26		[-1; 6]
12		[1; 4]	27		[-1; 7]
13		[1; 5]	28	3x/(x2+3)	[-4; 2]
14	-x2/4+8/x+5	[-4; -1]	29		[-2; 4]
15		[-3; 1]	30		[-5; 3,8]

Задание 6.2. Решить СНЛУ F(X)=0 методом простой итерации (=110^-3).

№ п/п	F(X)=0	№ п/п	F(X)=0
1	2	3	4
1		16

1	2	3	4
2		17
3		18
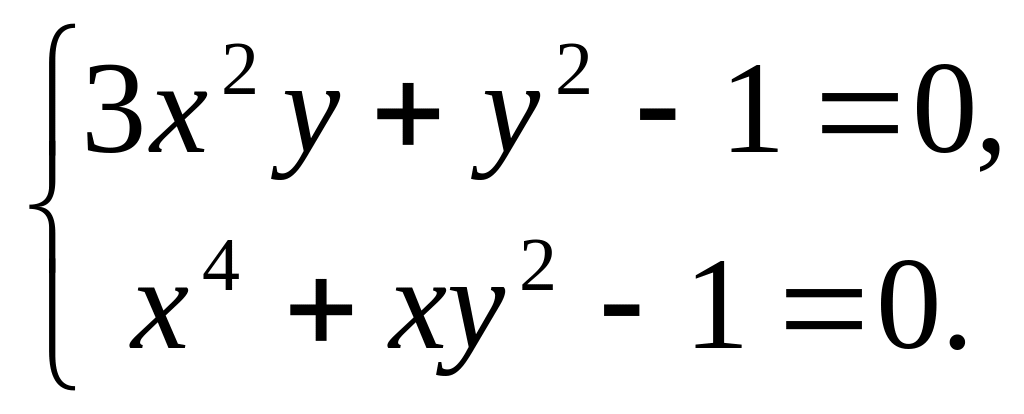
4		19
5		20
6		21
7		22
8		23
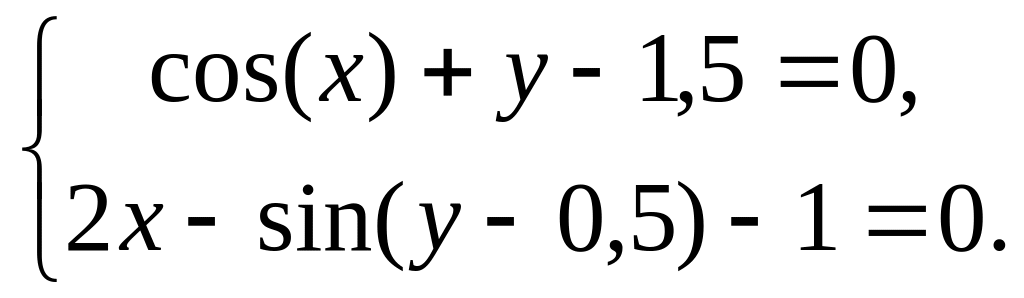
9		24
10		25
11		26
12		27
13		28
14		29
15		30

Задание 6.3. Решить СНЛУ F(x)=0 методом Зейделя.

Задание 6.4. Решить СНЛУ F(x)=0 методом Ньютона.