Лабораторная работа № 5 численное решение систем линейных алгебраических уравнений

Цель работы

1. Знакомство с задачами исследования и численными методами решения систем линейных алгебраических уравнений (СЛАУ).

2. Разработка численной ММ, реализующей один из методов.

3. Решение задач исследования однородных и неоднородных СЛАУ при помощи средств MATLAB.

Решение систем линейных уравнений – одна из наиболее часто встречающихся задач в научных и инженерных расчетах. Многие приложения приводят к этой задаче непосредственно, кроме того системы линейных уравнений могут возникать как один из этапов в решении более сложных проблем. При этом обычно число уравнений равно числу неизвестных. Такую систему можно записать в матричном виде A x=b, где А – заданная квадратная матрица порядка n, b – заданный вектор-столбец с n компонентами и x – неизвестный вектор-столбец с n компонентами. В свернутом виде система может быть записана как , i=1,2,…,n. Тогда в развернутом виде

a₁₁ x₁+ a₁₂ x₂ +…+ a_1n x_n =b₁,

a₂₁ x₁+ a₂₂ x₂ +…+ a_2n x_n =b₂,

……………………………………

a_n1 x₁+ a_n2 x₂ +…+ a_nn x_n =b_n .

Решением системы является вектор X^*={x₁*, x₂*,…, x_n*} при подстановке которого в каждое уравнение системы получаем истинные равенства. Для решения СЛАУ применяют прямые (точные) и итерационные (приближенные) методы. Метод решения задачи относится к классу точных, если предполагается отсутствие округлений и с его помощью можно найти решение в результате конечного числа арифметических и логических операций.

Среди прямых методов (используют конечное число преобразований системы) можно выделить методы Крамера, Гаусса, Гаусса-Жордана и др. Обычно их применяют для систем небольшой размерности (до 10³).

В частности, метод Гаусса (гауссовых исключений) состоит в приведении исходной системы путем последовательных исключений неизвестных (при помощи элементарных операций над строками: перестановка строк; умножение строки на число отличное от нуля; сложение строк) к эквивалентной системе с треугольной (ступенчатой) матрицей (прямой ход метода Гаусса)

x₁+ с₁₂ x₂ +…+ с_1n x_n =d₁,

c₂₂ x₂ +…+ c_2n x_n =d₂,

…………………

x_n =d_n ,

далее ее решают по рекуррентным формулам

x_n =d_n , , i=n-1,n-2,…, 1.

Итерационные методы реализуют стратегию постепенного приближения к решению X^* путем построения соответствующей последовательности векторов X⁰, X¹,…, X^k. Вектор X⁰ называется начальным приближением, а переход от текущего k-го приближения (вектор X^k ) к k+1-му приближению (вектор X^k+1) итерацией. Данный переход реализуется при помощи функционального оператора X^k+1=F(X^k), вид которого определяется заданной системой и конкретным методом.

Для итерационных методов (метод простой итерации, метод Зейделя и др.) решение получают всегда приближенным, в то же время необходимо отметить ряд преимуществ, которыми обладают последние по сравнению с прямыми методами:

1) меньшие затраты времени при получении решения;

2) значительно меньшие погрешности округления;

3) самоисправление случайных ошибок на очередном шаге;

4) особенная эффективность при работе с разряженными матрицами (большое количество коэффициентов которых равно нулю), а также для систем большой размерности (10³-10⁶).

Метод простой итерации реализует переход к k+1-му приближению, используя при определении каждой координаты нового вектора координат только предыдущего k-го приближения X^k+1=F(X^k). Пусть дана СЛАУ вида

a₁₁ x₁+ a₁₂ x₂ +…+ a_1n x_n + a_1n+1 =0,

a₂₁ x₁+ a₂₂ x₂ +…+ a_2n x_n + a_2n+1 =0, (1)

……………………………………

a_n1 x₁+ a_n2 x₂ +…+ a_nn x_n + a_nn+1 =0 .

Выразив из каждого уравнения соответствующую координату, получим

x₁=с₁₁ x₁+ с₁₂ x₂ +…+ с_1n x_n + с_1n+1,

x₂=с₂₁ x₁+ с₂₂ x₂ +…+ с_2n x_n + с_2n+1, (2)

……………………………………

x_n=с_n1 x₁+ с_n2 x₂ +…+ с_nn x_n + с_nn+1 .

Для обеспечения условий сходимости (сходимость или устойчивость метода обеспечивается при любом начальном приближении X⁰, если норма матрицы, составленной из коэффициентов только при неизвестных в системе (2) меньше единицы, т.е., например, при i=1,2,…,n) при переходе от системы (1) к системе (2) можно воспользоваться следующими преобразованиями:

,

где .

Если после данных преобразований сходимость не обеспечивается (единичные случаи), исходную систему необходимо преобразовать в эквивалентную. Это достигается путем попарного сложения или вычитания уравнений.

Далее текущее приближение X^k подставляют в правую часть системы (2), тогда в левой части получают координаты нового уточненного приближения X^k+1. В качестве начального приближения X⁰ можно выбрать столбец свободных членов b или нулевой вектор. Окончанием итерационного процесса может служить выполнение условия

,

где  – заданная погрешность приближенного решения.

Метод Зейделя является модификацией метода простой итерации. В целях ускорения сходимости он реализует переход к k+1-му приближению, используя при определении координат нового вектора не только предыдущее k-е приближение, но и вычисленные на данный момент координаты k+1-го приближения X^k+1=F(X^k, X^k+1):

x₁^k+1=с₁₁ x₁^k+ с₁₂ x₂^k+…+ с_1n-1 x_n-1^k +с_1n x_n^k+ с_1n+1,

x₂^k+1=с₂₁ x₁^k+1+ с₂₂ x₂^k+…+ с_2n x_n^k + с_2n+1,

……………………………………

x_n^k+1=с_n1 x₁^k+1+ с_n2 x₂^k+1+…+ с_nn x_n^k + с_nn+1 .

Дальнейшее ускорение сходимости последовательности приближений достигается в методе последовательной верхней релаксации. Для специального вида матриц, например симметричных, положительно определенных, имеется также семейство методов сопряженных градиентов или сопряженных направлений [3].

В целом для обеспечения сходимости итерационного метода достаточно, чтобы выполнялось условие ||A||<1, или ||С||<1 по какой-либо норме матрицы, согласованной с нормой векторов. Если для векторов x=(x₁,x₂,…,x_n) введена норма ||x||, то согласованной с ней нормой матриц называют величину . Чаще всего используют следующие нормы векторов и соответствующих согласованных норм матриц:

№ п/п	Норма вектора	Согласованная норма матрицы
1
2
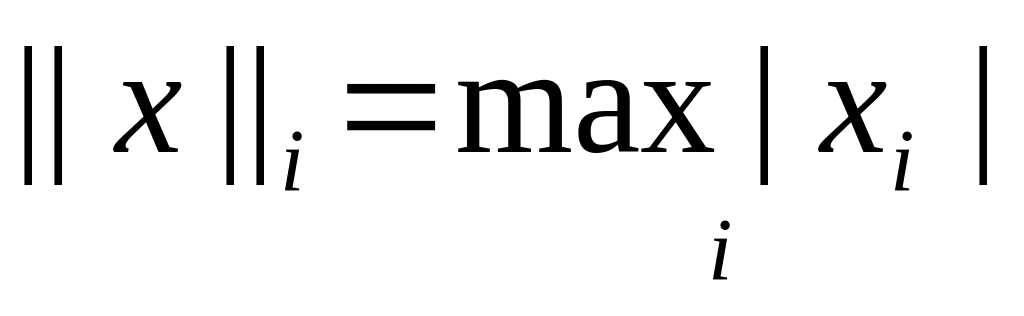
3		или с учетом ||A||2||A||e

где максимальное собственное значение матрицы .

В общем случае система может включать m уравнений относительно n неизвестных

a₁₁ x₁+ a₁₂ x₂ +…+ a_1n x_n =b₁,

a₂₁ x₁+ a₂₂ x₂ +…+ a_2n x_n =b₂,

……………………………………

a_m1 x₁+ a_m2 x₂ +…+ a_{m n} x_n =b_m .

Тогда данная система совместна, если она имеет хотя бы одно решение и несовместна, если не имеет ни одного.

Однородной СЛАУ называется система, правая часть которой равна нулю (b=0). Однородная система всегда совместна, т.к. имеет, по крайней мере, одно решение (x₁=0,…, x_n=0). Если однородная система имеет единственное решение, то оно нулевое и система называется тривиально совместной. Если имеется более одного решения, то среди них есть ненулевые. В этом случае говорят о нетривиально совместной системе. Такая система имеет бесконечное множество решений, причем линейная комбинация любых решений системы тоже является ее решением. Доказано, что среди бесконечного множества решений однородной системы можно выделить ровно n-r линейно независимых решений, где r – ранг матрицы А (число ненулевых строк в ступенчатой матрице, получаемой из исходной матрицы А с помощью гауссовых исключений).

Совокупность этих n-r линейно независимых решений называется фундаментальной системой решений. Любое решение СЛАУ линейно выражается через фундаментальную систему. Поэтому, если ранг r матрицы А однородной системы Аx=0 меньше числа неизвестных n, то система является нетривиально совместной и для любого решения системы с учетом векторов е₁, е₂,…, е_n-r, образующих ее фундаментальную систему решений (А е_i =0, i=1,2,…,n-r) можно записать выражение:

x=c₁ е₁ +c₂ е₂ +…+c_n-r е_n-r ,

где c₁, c₂,…, c_1n-r – произвольные постоянные, а само выражение называют общим решением однородной системы.

Исследовать однородную СЛАУ – это значит установить, является ли она нетривиально совместной и в этом случае найти фундаментальную систему решений, а также общее решение системы.

Неоднородной СЛАУ называется система, правая часть которой неравна нулю (b0). Для того, чтобы неоднородная система была совместна, необходимо и достаточно, чтобы ранг расширенной матрицы системы совпадал с рангом матрицы системы. Расширенная матрица получается путем добавления к матрице А столбца b.

Исследовать неоднородную СЛАУ – это значит установить, является ли она совместной, и если да, то найти общее решение системы.