Вопросы к экзамену по дисциплине

«Теория электрических цепей»

1. 1. Методы расчета электрических цепей постоянного тока. Активные и пассивные элементы цепей постоянного тока (источники и нагрузки). Закон Ома для участка цепи.

2. 2. Законы Кирхгофа в цепях постоянного тока. Баланс мощностей по постоянном и переменном токе. Резистивные делители напряжения и тока.

3. 3. Методы расчеты электрических цепей: контурных токов и узловых потенциалов.

4. 4. Методы расчеты электрических цепей: метод эквивалентного генератора и принцип суперпозиции.

5. 5. Основные параметры гармонического сигнала.

6. 6. Закон Ома и законы Кирхгофа для мгновенных значений токов и напряжений. Законы Ома и Кирхгофа в символической и операторной формах.

7. 6. Изображение синусоидальных ЭДС, напряжений и токов с помощью вращающихся векторов и комплексных чисел. Формулы Эйлера для комплексных чисел. Сложение, вычитание, умножение, деление синусоидальных функций времени. Векторная диаграмма.

8. 7. Зависимости между током и напряжением в цепи, содержащей только активное сопротивление; в цепи, содержащей только индуктивность; в цепи, содержащей только электроемкость.

9. 8. Ток и напряжение в цепи синусоидального тока при последовательном соединении R,L,C. Векторная диаграмма.

10. 9. Ток и напряжение в цепи синусоидального тока при параллельном соединении R,L и C. Векторная диаграмма.

1. 10. Мощности. Мгновенная мощность. Активная, реактивная и полная мощности. Коэффициент мощности. Треугольник мощностей.

2. 11. Три вида формул для мощности. Выражение мощности в символической форме. Условие передачи максимальной мощности от источника энергии нагрузке.

3. 12. Индуктивно-связанные цепи. Коэффициенты, характеризующие индуктивно-связанную систему. Согласное и встречное включение катушек. Трансформатор.

4. 13. Расчет электрических цепей при несинусоидальных периодических ЭДС, напряжениях и токах. Ряд Фурье. Спектры периодических сигналов. Действующие значения и мощности сигналов несинусоидальной формы.

5. 14. Классический метод расчета переходных процессов. Законы коммутации.

6. 15. Расчет переходных процессов операторным методом. Формула разложения для перехода от изображения к функции времени.

7. 16. Резонанс напряжений. Параметры и характеристики последовательного колебательного контура при резонансе напряжений. Векторная диаграмма.

8. 17. Резонансные кривые и частотные характеристики последовательного колебательного контура. Полоса пропускания и избирательность контура.

9. 18. Резонанс токов. Резонансная частота. Признаки резонанса токов. Векторная диаграмма. Добротность и входное сопротивление параллельного контура при резонансе.

10. 19. АЧХ и ФЧХ параллельного контура. Избирательность.

11. 20. Нелинейные резистивные цепи. Графические методы расчета, метод пересечений, метод эквивалентного генератора, итерационный метод.

12. 21. Нелинейное сопротивление при гармоническим воздействии. Понятие о режиме малого и большого сигнала. Нелинейное сопротивление при одновременном воздействии двух гармонических сигналов.

13. 22. Расчет переходных процессов с помощью интеграла Дюамеля. Временные и импульсные характеристики линейных цепей. Свертка двух функций.

14. 23. Дифференцирующие цепи. ФВЧ.

15. 24. Интегрирующие цепи. ФНЧ.

16. 25. Методы математического описания электрических цепей: дифференциальными уравнениями, в операторном виде и в частотной форме.

17. 26. Частотные характеристики электрических цепей. Пример их получения.

18. 27. Математическое описание линейных электрических цепей во временной области: типовые входные воздействия, переходная и импульсная переходная характеристики, примеры их расчёта и связь с другими способами мат. описания эл. цепей.

19. 28. Алгоритм расчета выходного сигнала линейной электрической цепи при произвольном входном воздействии по известным частотным харатеристикам эл. цепи (метод гармонического анализа).

ОТВЕТЫ

1.Методы расчета электрических цепей постоянного тока. Активные и пассивные элементы цепей постоянного тока (источники и нагрузки). Закон Ома для участка цепи.

Методы Расчета:

1. Метод уравнений Кирхгофа

Этот метод является наиболее общим методом решения задачи анализа электрической цепи. Он основан на решении системы уравнений, составленных по первому и второму законам Кирхгофа относительно реальных токов в ветвях рассматриваемой цепи. Следовательно, общее число уравнений p равно числу ветвей с неизвестными токами. Часть этих уравнений составляется по первому закону Кирхгофа, остальные – по второму закону Кирхгофа. В схеме содержащей q узлов, по первому закону Кирхгофа можно составить q уравнений. Однако, одно из них (любое) является суммой всех остальных. Следовательно, независимых уравнений, составленных по первому закону Кирхгофа, будет  .

По второму закону Кирхгофа должны быть составлены недостающие m уравнений, число которых равно  .

Для записи уравнений по второму закону Кирхгофа необходимо выбрать m контуров так, чтобы в них вошли в итоге все ветви схемы.

Первый закон Кирхгофа

В любом узле электрической цепи алгебраическая сумма токов равна нулю

,

где m – число ветвей подключенных к узлу.

При записи уравнений по первому закону Кирхгофа токи, направленные к узлу, берут со знаком «плюс», а токи, направленные от узла – со знаком «минус». Например, для узла а (см. рис. 1.2) I−I₁−I₂=0.

Второй закон Кирхгофа

В любом замкнутом контуре электрической цепи алгебраическая сумма ЭДС равна алгебраической сумме падений напряжений на всех его участках

,

где n – число источников ЭДС в контуре; m – число элементов с сопротивлением R_k в контуре; U_k=R_kI_k – напряжение или падение напряжения на k-м элементе контура.

2.Метод контурных токов

Метод контурных токов сводится к составлению уравнений только по второму закону Кирхгофа. Число этих уравнений, равное  , на   уравнений меньше числа уравнений, необходимых для расчета электрических цепей по методу законов Кирхгофа.

При этом предполагаем, что в каждом выбранном контуре протекает независимые друг от друга расчетные токи, называемые контурными. Ток каждой ветви определяется как алгебраическая сумма контурных токов, замыкающихся через эту ветвь, с учетом принятых направлений контурных токов и знаков их величин.

Число контурных токов равно числу «ячеек» (элементарных контуров) схемы электрической цепи. Если рассматриваемая схема содержит источник тока, то независимые контуры необходимо выбирать так, чтобы ветвь с источником тока входила только в один контур. Для этого контура расчетное уравнение не составляется, так как контурный ток равен току источника.

Каноническая форма записи уравнений контурных токов для n независимых контуров имеет вид

где

 - контурный ток n-го контура;

- алгебраическая сумма ЭДС, действующих в n-ом контуре, называемая контурная ЭДС;

- собственное сопротивление n-го контура, равная сумме всех сопротивлений, входящих в рассматриваемый контур;

 - сопротивление принадлежащие одновременно двум контурам (в данном случае контуром n и i) и называемое общим или взаимным сопротивлением этих контуров. Первым ставится индекс контура, для которого составляется уравнение. Из определения взаимного сопротивления следует, что сопротивления, отличающиеся порядком индексов, равны, т.е.  .

Взаимным сопротивлением приписывается знак плюс, если протекающие по ним контурные токи   и   имеют одинаковые направления, и знак минус, если их направления противоположны.

Таким образом, составление уравнений контурных токов может быть сведено к записи симметричной матрицы сопротивлений

и вектора контурных ЭДС

При введении вектора искомых контурных токов | | уравнения (5) можно записать в матричной форме

Решение системы линейных уравнений алгебраических уравнений (5) для тока n-го контура может быть найдено по правилу Крамера

,

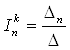где   - главный определитель системы уравнений, соответствующий матрице контурных сопротивлений