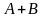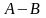Лабораторная работа № 4 множества
Цель работы: Овладеть понятиями множество и элементы множеств; изучить способы задания множеств; изучить операции, производимые над множествами, применить усвоенные знания на практике.
Теоретические сведения
Наряду с численными типами множества являются фундаментальным понятием в математике (конечные, бесконечные, состоящие из разных (произвольных) элементов). В Pascal рассматриваются только конечные множества, состоящие из небольшого числа элементов имеющие один и тот же тип.
Множества в– это ограниченный, упорядоченный набор различных элементов одного базового типа.
Базовый тип – это совокупность значений, из которых могут быть образованы множества. Всего может быть не более 256 различных элементов. (Идет то же самое расширение, что и по строке.)
Постоянные множества (множества-константы) и в Pascal и в математике задаются путем их перечисления.
-
Математика
Pascal
0
[]
{1, 2, 3}
[1, 2, 3]
{A, B, C, D}
['A', 'B', 'C', 'D']
{1, 2, …, N}
[1..N]
В квадратных скобках могут указываться не только константы, но и выражения типа элементов множества.
Множества в Pascal описываются:
TYPE имя типа = SET OF базовый тип;
VAR имя переменной: имя типа;
или
VAR имя переменной: SET OF базовый тип;
или
CONST имя переменной = [элементы множества];
Пример:
VAR A: SET OF INTEGER;
B: SET OF 'A'..'Z';
C: SET OF CHAR;
В отличие от массивов к элементам множества нет прямого доступа, поэтому ввод и вывод элементов множества осуществляется:
Ввод с помощью операции сложения (объединения)
Вывод с помощью проверки принадлежности IF.
Формирование множеств
Если элементы множества идут подряд друг за другом, то можно использовать диапазон. Например, множество описанное: VAR A: SET OF 1..5; может принимать значения:
A = [];
A [1],
[2], [3], [4], [5]
[1],
[2], [3], [4], [5]
A [1, 2], [1, 3], [1, 4], [1, 5]…
A [1, 2, 3]…
A [1, 2, 3, 4]…
A [1, 2, 3, 4, 5]
Отношения и операции над множествами
-
Математика
Pascal

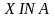

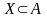



В Pascal определены операции над множествами:
1. Объединение Математика:
Pascal:
Объединением двух множеств называется множество элементов принадлежащих обоим множествам. Пример: ['A', 'B'] + ['C', 'D'] = ['A', 'B', 'C', 'D'] |
|
2. Пересечение Математика:
Pascal:
Пересечением двух данных множеств называется множество элементов принадлежащих одновременно и первому и второму множеству, общие элементы. Пример: ['A', 'B']*['C', 'D'] = []; |
|
3. Исключение Математика:
Pascal:
Вычитанием двух множеств называется множество, состоящее из тех элементов первого множества, которые не являются элементами второго множества. Пример: ['A', 'B'] – ['C', 'D'] = ['A', 'B']; |
|
Над значениями множественного типа определены и некоторые операции отношения. Операндами операций над множественными значениями в общем случае являются множественные выражения. Среди операций отношения над значениями множественного типа особое место занимает специальная операция проверки вхождения элемента во множества, обозначаемая служебным словом in. В отличие от остальных операций отношения, в которых значения обоих операндов относятся к одному и тому же множественному типу значений, в операции in первый операнд должен принадлежать базовому типу, а второй – множественному типу значений, построенному на основе этого базового типа. Результатом операции отношения, как обычно, является логическое значение (true или false).
‘a’ in glasn значение операции true;
‘o’ in soglasn значение операции false;
Операция сравнения на равенство множественных типов Паскаля. Множества считаются равными (эквивалентными), если все элементы одного множества присутствуют в другом и наоборот. Для операции сравнения на равенство или неравенство используются символы ‘=’ и ‘<>’.
A:= [2,1,3];
D:= [1,3,2];
Тогда операция A=D имеет значение true, а операция A<>D имеет значение false.
Проверка включения. Одно множество считается включенным в другое (одно множество является подмножеством другого), если все его элементы содержатся во втором множестве. Обратное утверждение может быть и несправедливым. Операции проверки включения обозначаются ‘<=’ и ‘>=’.
letter >= glasn;
soglan <= letter;
Для добавления множеству нового элемента в Паскаль есть операция Include:
Include(<множество>, <элемент>)
Для удаления из множества какого-либо элемента можно воспользоваться операцией Exclude:
Exclude(<множество>, <элемент>)
Необходимо помнить, что добавляемый/удаляемый элемент должен быть тождественного множеству типа.
Все значения множества представляются в памяти последовательностями битов одинаковой длины. За каждое значение базового типа "отвечает" один бит. Если множество содержит некоторый элемент, в "ответственном" за него бите хранится 1, если не содержит - хранится 0.
Внутреннее представление X
x:=[]; 000000000000000>
x:=[2,3,5]; 011010000000000>
x:=[1..15]; 111111111111111>
Операции над множествами сводятся к поразрядным логическим операциям над последовательностями битов, пример, объединение множеств выполняется путем поразрядного логического сложения битов:
x:=[2,3,5]; 011010000000000>
y:=[3,5,7,8]; 001010110000000>
z:=x+y; 011010110000000>
Поразрядные документы входят в набор команд процессора ЭВМ, поэтому выполняется быстро.
Средства работы с множествами позволяют в некоторых случаях сократить программы и сделать их более наглядными и эффективными за счет уменьшения числа проверок.