ЗМІСТ

ВСТУП

1. ЗАВДАННЯ НА КУРСОВИЙ ПРОЕКТ

2 ВПЛИВ ПОЛЮСІВ НА ВИГЛЯД ПЕРЕХІДНОГО ПРОЦЕСУ

3 СИНТЕЗ САК

3.1 Параметричний синтез регулятора системи

з одиничним зворотним зв’язком

3.2 Синтез регулятора струму з урахуванням

коефіцієнта датчика струму

3.3 Критерії оптимальності. Загальні теоретичні положення.

3.4 Синтез регулятору струму за технічним критерієм оптимізації.

3.5 Синтез регулятору швидкості.

ВСТУП

Виконання курсового проекту з дисципліни „Теорія автоматичного керування” є одним із важливих етапів формування фахівця зі спеціальності «Електромеханічні системи автоматизації та електропривод».

Метою курсового проекту є придбання практичних навичок аналізу і синтезу систем автоматичного керування.

Під час виконання курсового проекту студенти користуються методом синтезу, що спирається на забезпеченні наперед заданих характеристик перехідного процесу (за Баттервортом, Бесселем, біноміальним розподіленням, симетричним та технічним критеріями) шляхом формування характеристичного поліному замкненої електромеханічної системи.

У методичних вказівках надані практичні рекомендації щодо виконання курсового проекту, що можуть бути використані при виконанні спецчастини дипломного проекту.

Пояснювальна записка повинна містити:

• завдання на виконання курсового проекту.

• Вихідні данні (табл. 5).

• Синтез регулятору струму за умови наявності одиничного зворотного зв’язку шляхом оптимізації контуру струму за наступними стандартними розподіленнями полюсів: Бесселя, Баттерворта, біноміального розподілення.

• Синтез регулятору струму з урахуванням коефіцієнта перетворення датчика струму в зворотному зв’язку, шляхом оптимізації контуру за розподіленням полюсів за Баттервортом.

• Синтез регулятору струму за технічним оптимумом.

• Порівняльний аналіз перехідних процесів в контурі струму, що оптимізований за критеріями Бесселя, Баттерворта, біноміального розподілення коренів і за технічним оптимумом.

• Синтез регулятору швидкості шляхом оптимізації контуру швидкості за технічним оптимумом.

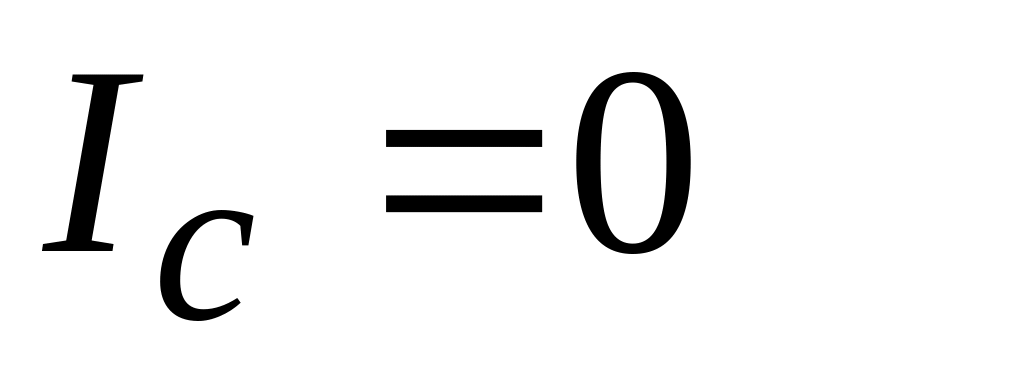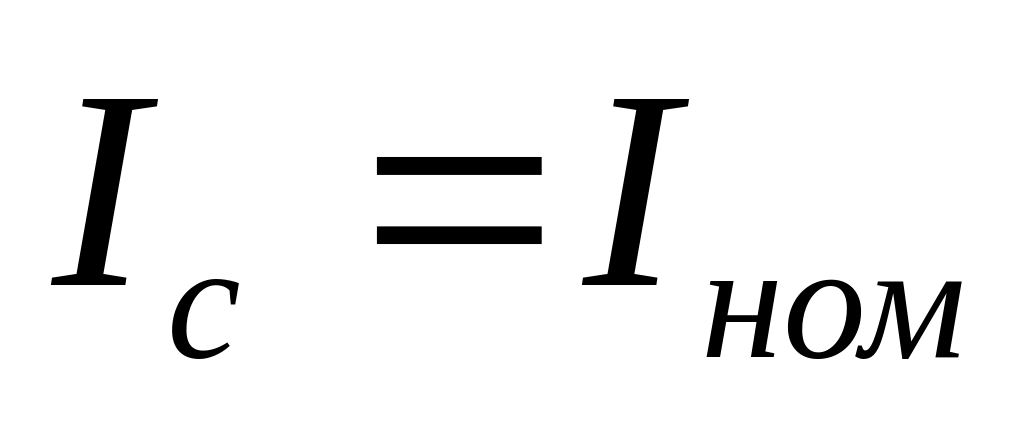• Аналіз реакції оптимізованого контуру швидкості на ступінчастий сигнал керування амплітудою 10 вольт поданого на вхід контуру за умови наявності ступінчастого навантаження (від до ). Ступінчасте навантаження подається до контуру після закінчення перехідного процесу за швидкістю.

• Синтез регулятору швидкості шляхом оптимізації контуру швидкості за симетричним оптимумом.

• Аналіз реакції оптимізованого контуру швидкості на ступінчастий сигнал керування амплітудою 10 вольт поданого на вхід контуру за умови наявності ступінчастого навантаження (від до ). Ступінчасте навантаження подається до контуру після закінчення перехідного процесу за швидкістю.

• Порівняльний аналіз систем автоматичного керування з П – і ПІ – регуляторами швидкості.

• Визначення передатних функцій замкненого контуру швидкості з П – і ПІ – регуляторами за каналами керування та збурення. Аналітичне визначення статичної помилки за швидкістю системи електропривода постійного струму.

Графічна частина повинна містити:

• перехідний процес при відпрацюванні контуром струму з одиничним зворотнім зв’язком ступінчастого сигналу завдання амплітудою 10 вольт, поданого на вхід контуру, для кожного з критеріїв оптимізації: Баттерворта, Бесселя, біноміального розподілення коренів.

• Перехідний процес при відпрацюванні контуром струму ступінчастого сигналу завдання амплітудою 10 вольт, поданого на вхід системи. Контур струму оптимізований за Баттервортом з урахуванням коефіцієнта перетворення датчика струму в зворотному зв’язку.

• Перехідний процес в контурі струму, що оптимізований за технічним оптимумом при відпрацюванні ступінчастого сигналу завдання амплітудою 10 вольт поданого на вхід системи.

• Перехідні процеси за швидкістю й струмом в контурі швидкості з П – регулятором при відпрацюванні ступінчастого сигналу завдання амплітудою 10 вольт поданого на вхід системи. Ступінчасте навантаження від до подається до контуру після закінчення перехідного процесу за швидкістю. Перехідні процеси за струмом й швидкістю наводяться у спільній системі координат.

• Перехідні процеси за швидкістю й струмом в контурі швидкості з ПІ – регулятором при відпрацюванні ступінчастого сигналу завдання амплітудою 10 вольт поданого на вхід системи. Ступінчасте навантаження від до подається до контуру після закінчення перехідного процесу за швидкістю. Перехідні процеси за струмом й швидкістю наводяться у спільній системі координат.

• Для кожного з методів оптимізації контурів струму й швидкості за допомогою пакету «MATLAB» отримати й роздрукувати у спільній системі координат амплітудно-частотні характеристики (ЛАЧХ) і фазочастотні характеристики (ФЧХ):

• об’єктів керування (контур струму, контур швидкості);

• замкненої системи, що є оптимізованою за певним критерієм;

• самого регулятора координати.

1. Завдання на курсовий проект

Виконати синтез системи автоматичного керування швидкістю (САК) електроприводу постійного струму (табл. 5).

Структура розроблювальної системи побудованої за замкнутим принципом, зображена на рис.1.1.

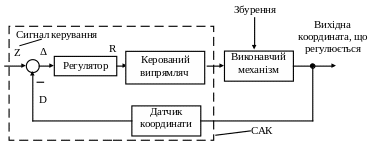
Рис. 1.1 Система автоматичного керування

Під час розрахунку системи автоматичного керування електроприводу постійного струму необхідно:

1. Отримати передатні функції тиристорного перетворювача, двигуна постійного струму.

2. Записати й визначити параметри передатної функції об’єкту керування в контурі струму. Розрахувати коефіцієнт перетворення датчика струму.

3. Виконати синтез регулятора струму за умови наявності одиничного зворотного зв’язку в контурі. Оптимізацію контуру слід виконувати за Баттервортом, Бесселем, біноміальним розподіленням.

4. Виконати синтез регулятора струму з урахуванням зворотного зв’язку в контурі. Оптимізацію контуру слід виконувати за Баттервортом.

5. Виконати синтез регулятора струму з урахуванням зворотного зв’язку в контурі. Оптимізацію контуру слід виконувати за технічним критерієм.

6. Для кожного з критеріїв оптимізації створити в «Simulink» математичну модель контуру струму.

7. Дослідити й порівняти перехідні процеси за усіма критеріями оптимізації при відпрацюванні контуром струму сигналу завдання амплітудою 10 вольт.

8. Виконати синтез регулятору швидкості користуючись технічним критерієм.

9. Виконати синтез регулятору швидкості користуючись симетричним критерієм.

10. Для кожного з критеріїв оптимізації створити в «Simulink» математичну модель контуру швидкості з підпорядкованим контуром струму. Підпорядкований контур струму повинен містити ПІ – регулятор, що розрахований за технічним критерієм (див. п.5).

11. Дослідити й порівняти перехідні процеси за швидкістю й струмом при відпрацюванні контуром швидкості з підпорядкованим контуром струму сигналу завдання що наведений на рис. 3.16, за умови наявності ступінчастого навантаження (від до ). Ступінчасте навантаження подається до системи після закінчення перехідного процесу за швидкістю (рис. 3.17).

12. Визначити передатні функції замкненого контуру струму й швидкості за різних критеріїв оптимізації.

13. За допомогою «MATLAB» отримати для різних критеріїв оптимізації ЛАЧХ, ФЧХ об’єків керування (для контуру струму й контуру швидкості), регуляторів та замкнених контурів струму й швидкості.

14. Записати результати розрахунку курсового проекту до таблиці 6.

2 Вплив полюсів на вигляд перехідного процесу

Розташування полюсів на комплексній площині зумовлює характеристики перехідного процесу, динамічні показники якості. Перед синтезом регулятора необхідно виконати побудову еталонної моделі системи керування, яка забезпечує бажане розподілення на комплексній площині коренів характеристичного рівняння замкненої системи. Отже, постає питання яке розташування коренів вибрати?

Якщо передатна функція замкненої системи не має нулів, то при виборі її бажаного полінома можна керуватися стандартними формами (фільтрами), які знайшли широке розповсюдження на практиці. Стандартні форми визначають коефіцієнти характеристичного полінома (знаменника), що забезпечують перехідні процеси з відомими показниками якості. Якщо ж система характеризується наявністю нулів, стандартні форми можуть служити як вихідний матеріал для пошуку оптимального розташування коріння.

В характеристичному поліномі спочатку виділяються полюси для компенсації нулів, а поліном, що залишився, формується виходячи з умови бажаного розташування коренів.

Якість роботи системи керування визначається точністю в сталому режимі, й формою перехідного процесу. При дослідженні перехідних процесів частіше вважають, що вхідний сигнал є функцією Хевісайда. В цьому випадку крива перехідного процесу називається перехідною функцією і характеризується показниками, що приймаються за міру якості системи керування (рис. 2.1):

• час наростання 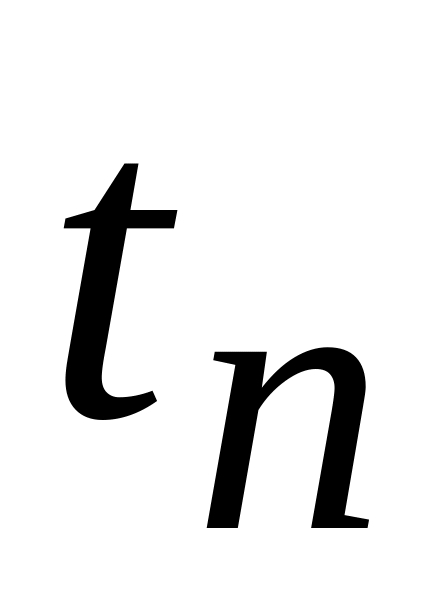- час, необхідний для досягнення 95% кінцевого значення;

• час керування 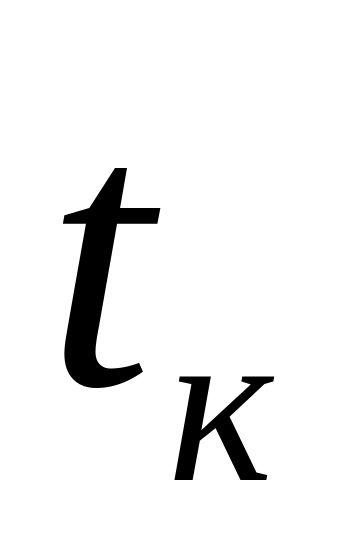- час за який коливання керуємої координати зменшаться до деякого значення (рис. 2.1);

• перерегулювання – різниця між максимальним значенням керованої величини і її сталого рівня (% від сталого рівня);

• пульсації - число коливань до виходу кривої в сталий режим.

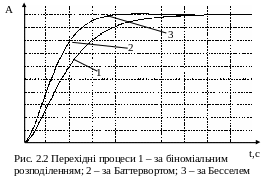
Типові перехідні характеристики для різних фільтрів при вхідному сигналі у вигляду функції Хевісайда якісно представлені на рис. 2.2.

Розглянемо характеристичне рівняння:

; яке запишемо у вигляді:

.

За виразами Вієта визначається як сума всіх коренів рівняння. В загальному вигляді . При необхідності, можливо задати потрібне розташування коренів характеристичного поліному на комплексній площині виходячи з вимог динаміки. У випадку, коли корені дійсні й кратні, . Приймемо наступне позначення: , де - середньогеометричний корінь. З урахуванням викладеного вище запишемо:

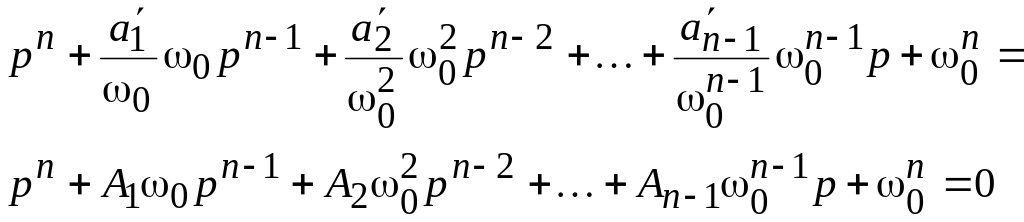
Розташування коренів характеристичного рівняння визначається величиною , що пов’язана з розташуванням точки на дійсній вісі комплексної площини – геометричний центр всіх коренів системи. Коефіцієнт визначає взаємне розташування коренів. Слід зауважити, що визначає криву перехідного процесу в відносному часі , а величина масштабує час протікання перехідного процесу.

На рис.2.3 показано вплив зміни значення середньогеометричного кореня на форму і якість часових і частотних характеристик (на прикладі фільтру Баттерворта).

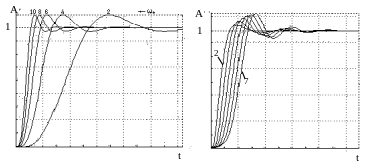
Рис. 2.3 Вплив середньогеометричного кореня на перехідні характеристики (а) й ступеня системи (б)

Зростання сприяє поліпшенню динаміки системи завдяки зменшення часу наростання і часу встановлення сигналу. Ступінь характеристичного полінома визначається порядком системи, що синтезується. Для фільтрів високого порядку реальні АЧХ значно покращуються (рис. 2.4). Однак слід пам’ятати, що високий порядок викликає ускладнення схемної реалізації пристроїв. Синтез передбачає розв’язання задачі побудови системи управління мінімального порядку й вимагає правильного вибору порядку системи і розташування коренів на комплексній площині.

Розглянемо формування перехідних процесів за допомогою розглянутого підходу. Спочатку визначають бажаний вигляд перехідного процесу. Далі обирають бажане характеристичне рівняння з наперед заданими коефіцієнтами:

.

Наступним кроком визначимо характеристичне рівняння структурної схеми об’єкту керування: ,

де коефіцієнти, що пов’язані з параметрами системи.

Рис. 2.4 Залежність АЧХ (а) й ФЧХ (б) від середньогеометричного кореня (для фільтра Баттерворта)

Далі запишемо систему алгебраїчних рівнянь, дорівнюючи коефіцієнти рівнянь при однакових ступенях оператора Лапласа :

.

З

Таблиця 2

Порядок поліному	Поліном
1
2
3

урахуванням середньогеометричного кореня характеристичні поліноми моделі Бесселя набувають форми запису, що наведена у таблиці 1, а моделі Баттерворта та біноміального розподілення коренів у таблицях 2,3 відповідно.

Таблиця 1

Порядок поліному	Поліном
1
2
3

В

Таблиця 3

Порядок поліному	Поліном
1
2
3

игляд перехідних процесів для біноміального розподілення коренів при умові, що порядок поліному не перевищує 4 наведено на рис.2.5, а для моделей Баттервора та Бесселя на рис. 2.6, 2.7 відповідно. Розв’язуючи систему відносно параметрів регулятора, отримують параметри, які визначають наперед задані перехідні процеси.

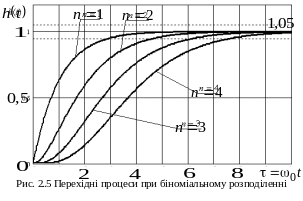
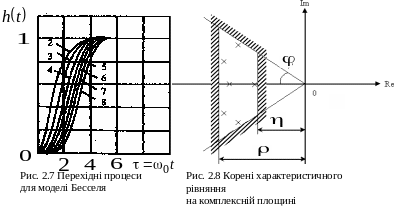
При необхідності можливо виконати приблизну оцінку якості перехідних процесів маючи вигляд розташування коренів на комплексній площині (рис. 2.8). До основних критеріїв, що характеризують перехідний процес відносяться (рис. 2.8): - показник тривалості, - показник коливальності (розраховується на основі ), - максимальна відстань кореня до уявної осі.

За допомогою оцінюють час протікання перехідного процесу за допомогою наступного співвідношення: , де - половина ширини області, в межах якої перехідний процес вважається завершеним. При маємо: (3.4).

Показник коливальності розраховується як: ,

де - дійсна й уявна частини комплексного кореня.

Дальню від уявної осі межу зумовлює показник , який визначають коріння, що практично не впливають на перехідний процес.

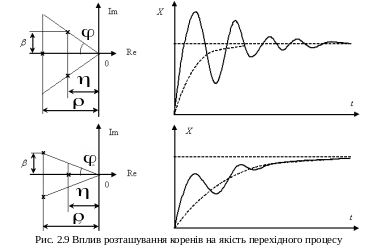
Вплив вище перелічених показників на форму перехідного процесу демонструє рис. 2.9.