7 Вопросы самопроверки для защиты лабораторной работы:

7.1 Объяснить формы кривых выходного напряжения?

7.2 В чем разница между пассивными и активными элементами цепей?

7.3 С какой целью вводятся цепи с ОС?

7.4 Докажите, что коэффициент передачи исследуемой цепи с ОС равен , а входное сопротивление - R₁?

9. Лабораторная работа №5 «Исследование неразветвленных цепей при гармоническом воздействии на постоянной частоте»

1 Цель работы: : Исследовать неразветвлённую RLC цепь при гармоническом воздействии на постоянной частоте

2 Задание:

2.1.Измерить напряжение всей цепи, напряжение на каждом элементе цепи, угол сдвига фаз между током и напряжением.

2.2.По результатам измерений рассчитать силу тока, полное, емкостное, индуктивное сопротивления, величину индуктивности и ёмкости.

2.3.Вычислить углы сдвига фаз между током и напряжением и сравнить их с измеренными фазометром.

2.4.Вычислить значения мощностей: резистивной Р, реактивных P_qc; P_ql; Pq, полной S.

2.5.Построить векторные диаграммы напряжений, треугольники сопротивлений и мощностей.

3 Литература: Добротворский И.Н. Теория электрических цепей. - М.: Радио и связь, 1989.-е. 109-118.

4 Краткие пояснения:

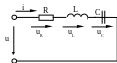
Рисунок 5.1 - Эквивалентная схема цепи с резистивным сопротивлением, индуктивность и емкостью.

Если неразветвлённую RLC-цепь подключить к генератору гармонического сигнала, то в ней установится синусоидальный ток.

i=I_msinωt (5.1)

Напряжение на резистивном сопротивлении совпадает по фазе с током.

u_R=U_Rmsinωt (5.2)

Напряжение на индуктивности, опережает ток по фазе на угол 90°.

u_L=U_Lmsin(ωt+π/2) (5.3)

Напряжение на ёмкости, отстаёт от тока по фазе на угол 90°

u_C=U_Cmsin(ωt-π/2) (5.4)

Амплитуда этих напряжений:

U_Rm=RI_m; U_Lm=ωLI_m=X_LI_m; U_Cm=(1/ωC)I_m=X_CI_m (5.5)

И их действующие значения

U_R=RI; U_L=ωLI=X_L.I; U_c=(l/ωC)I=X_CI (5.6)

Построить векторную диаграмму для случая X_L>X_C, то есть U_L>U_C.

φ>0 (5.7)

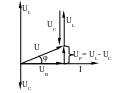
Рисунок 5.2 - Векторная диаграмма RLC-цепи при X_L>X_C

Мгновенное значение напряжения на зажимах рассматриваемой неразветвленной цепи равно сумме трех составляющих: резистивной, индуктивной и емкостной.

;

Напряжение на емкости изменяется в противофазе с напряжением на индуктивности и их алгебраическая сумма называется реактивной составляющей напряжения:

(5.8)

Абсолютное значение разности амплитудных значений напряжений U_Lm и U_Cm равно амплитуде реактивной составляющей напряжения U_Pm. Реактивная составляющая напряжения опережает по фазе резистивную на угол π/2, при U_L>U_C, то есть X_L>X_C (рисунок 5.2.) или отстаёт на угол π/2, при U_L<U_C, то есть X_L<X_C (рисунок 5.3.).

Напряжение на зажимах цепи равно сумме резистивной и реактивной составляющих.

(5.9)

Построим векторную диаграмму для случая X_L<X_C, т.е. U_L<U_C

φ<0 (5.10)

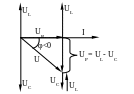
Рисунок 5.3 - Векторная диаграмма RLC-цепи при X_L<X_C

Действующее значение напряжения на зажимах RLC-цепи:

(5.11)

В дальнейшем реактивную составляющую U_P будем считать алгебраической величиной.

U_P=U_L-U_C (5.12)

U_P > 0 при U_L >U_C и U_P < 0 при U_L <U_C

Заменим в (5.11) напряжения U_P,U_L,U_C их выражениями:

(5.13)

где полное сопротивление цепи:

(5.14)

- реактивное сопротивление (алгебраическая величина в отличии от и ).

Полное сопротивление Z графически изображается гипотенузой прямоугольного треугольника сопротивлений при (рисунок 5.4.) построенный- при , одним катетом которого является резистивное сопротивление R, а другим модуль, реактивного сопротивления RLC-цепи.

(5.15)

При небольшой разнице между индуктивным и емкостным сопротивлениями каждое из них может быть значительно больше полного сопротивления RLC-цепи.

Для цепи, в которой реактивное сопротивление положительно, для цепи, у которой , реактивное сопротивление отрицательно.

Треугольники сопротивлений можно получить, разделив все стороны векторной диаграммы напряжений на ток I.

Рисунок 5.4. - Треугольник сопротивлений RLC-цепи при

Рисунок 5.5 - Треугольник сопротивлений RLC-цепи при

Угол сдвига фаз между напряжением и током равен углу между сторонами Z и R треугольника сопротивлений и определяется через тангенс.

(5.16)

или синус

(5.17)

В отличии от и угол - алгебраическая величина. При или при . (рисунок 5.2. и 5.4.) угол положительный. Это значит, что напряжение на зажимах RLC-цепи опережает по фазе ток на угол (цепь носит резистивно-нндуктивный характер.)

При или при угол равен нулю, напряжение и ток совпадают по фазе.(цепь носит резистивный характер), имеет место резонанс напряжений.

При или при (Рисунок 5.3. и 5.5.) угол отрицателен, напряжение отстаёт по фазе на угол (цепь носит резистивно-емкостной характер.)

Во всех случаях, как следует из векторной диаграммы напряжений (рисунок 5.2. и 5.3.)

(5.18)

Треугольник мощностей.

Если все стороны векторной диаграммы напряжений умножить на ток I, то получим подобный треугольник мощностей.

Рисунок 5.6 - Треугольник мощностей RLC-цепи при

Рисунок 5.7 - Треугольник мощностей RLC-цепи при

Средняя резистивная мощность:

(5.19)

Реактивная мощность (характеризует обмен энергией между цепью и источником питания):

(5.20)

Реактивная мощность может быть положительной (резистивно-индуктивный режим) ; ; φ<0.

Полная мощность:

(5.21)

Коэффициент мощности:

(5.22)